- DOI 10.31509/2658-607x-202142-3
- УДК 533.6
Математическое моделирование влияния лесного пожара на ветвь хвойного дерева
© 2021 Н. В. Барановский1, Д. С. Меньшиков2
1Томский политехнический университет,
Россия, 634050, г. Томск, пр. Ленина, 30
2Государственный специализированный проектный институт
Россия, 630075, г. Новосибирск, ул. Богдана Хмельницкого, 2
E-mail: firedanger@yandex.ru
Поступила в редакцию 17.02.2021
После рецензирования 14.06.2021
Принята к печати 29.06.2021
Необходима разработка количественных методов для оценки образования термических поражений морфологических частей хвойных деревьев. Цель исследования: математическое моделирование теплопереноса в слоистой структуре ветви хвойного дерева при воздействии фронта лесного пожара. Распространение тепла в системе «ветвь — хвоя —зона пламени» описано системой нестационарных дифференциальных уравнений теплопроводности с соответствующими начальными и граничными условиями. В качестве объекта исследования использована цифровая модель ветви хвойного дерева различных пород, а именно: сосны, лиственницы и пихты. Получены распределения температуры для различных вариантов строения ветви и условий воздействия фронта лесного пожара. Сделаны выводы о необходимости дальнейшей модернизации математической модели. Разработанная модель является базовой для создания программных инструментов для специализированных геоинформационных систем.
Ключевые слова: лесной пожар, ветвь, теплоперенос, воздействие, термическое повреждение
Лесные пожары в настоящее время представляют настоящее бедствие для ряда стран мирового сообщества, так как лесные пожары превратились из регулирующего фактора в катастрофическое явление. В результате лесных пожаров загрязняется атмосфера, гибнут древостои, происходит уничтожение запасов деловой древесины, обостряются хронические заболевания и уничтожаются сельские населенные пункты. Одна из важных проблем — это отмирание отдельных деревьев или целых древостоев в результате воздействия на них лесных пожаров (Baranovskiy, Kuznetsov, 2017; Baranovskiy, 2020). В настоящее время широко ведутся исследования в рамках количественной экологии, которая изучает динамику отдельных экологических систем и включает математические модели отдельных экологических процессов (Шилов, 2003). Существующие методы оценки экологических последствий лесных пожаров основаны главным образом на оценке статистического и фактического материала (Michaletz, Johnson, 2007; Yakimov, Ponomarev, 2020).
Термические поражения, полученные при лесном пожаре, могут запустить целый набор сложных механизмов изменения физиологии деревьев в послепожарный период (Bar et al., 2019). Последствия воздействия лесного пожара на деревья проявляются по-разному в зависимости от характеристик конкретного лесного пожара (Michaletz, Johnson, 2007; O’Brien et al., 2018). Верховые лесные пожары высокой интенсивности сжигают живую и мертвую биомассу в кроне дерева. Сгорание всей листвы или хвои и меристемы может вызвать немедленную гибель дерева, если дерево не способно дать ростки из термостойких органов (Clarke et al., 2013; Pausas, Keeley, 2017). Различают первичные и вторичные последствия лесных пожаров (Michaletz, Johnson, 2007). Первичные последствия являются прямым следствием теплопереноса из зоны горения лесных горючих материалов в корневую систему, ствол и крону дерева (Michaletz, Johnson, 2007; Bergman, Incropera, 2011). Гибель тканей дерева, вызванная денатурацией протеина, происходит в общем случае при 60 C (Rosenberg et al., 1971). Однако скорость отмирания клеток увеличивается согласно экспоненциальному закону в зависимости от температуры. То есть, более низкие температуры тоже могут привести к гибели клеток в случае более длительного воздействия повышенной температуры (Hare, 1961; Dickinson, Johnson, 2004). Теплоперенос из зоны горения в крону дерева может вызвать немедленное омертвление почек или листвы, а также повреждение камбия и флоэмы ветвей. Степень повреждения компонентов кроны зависит от их теплофизических свойств и характеристик самого лесного пожара, а также высоты нижней границы кроны дерева (van Wagner, 1973; Michaletz, Johnson, 2006, 2007). В больших компонентах кроны типа ветвей присутствует внутренний температурный градиент и становится важным процесс теплопроводности внутри самого этого компонента. Скорость кондукции уменьшается с радиальной координатой, и поэтому важны толщина и свойства коркового слоя (Michaletz et al., 2013; Pounden et al., 2014). Вторичные последствия лесных пожаров более сложные, и их механизмы еще не до конца изучены. Отклик функций растительности на термические повреждения может различаться в широком диапазоне (Bar et al., 2019). С одной стороны, деревья после лесного пожара могут демонстрировать нарушение физиологической деятельности, снижение роста и замедленную гибель (Lambert, Stohlgren, 1988; van Mantgem, Schwartz, 2003; van Mantgem et al., 2011; Thompson et al., 2017). С другой стороны, известно, что травмированные деревья могут иметь преимущества в краткосрочный и среднесрочный период (Pearson et al., 1972; Battipaglia et al., 2014; Valor et al., 2018).
Однако необходима разработка математических методов оценки последствий воздействия поражающих факторов лесного пожара на деревья и отдельные их части. В частности, важно понимать процессы образования термического поражения ветви хвойного дерева. В связи с этим формулируется следующая цель исследования.
Цель работы: математическое моделирование теплопереноса в ветви хвойного дерева при воздействии повышенной температуры от фронта лесного пожара.
МАТЕРИАЛЫ И МЕТОДЫ
Объект исследования: хвойные деревья, а именно: сосна, лиственница, пихта (Лесотека, 2020). Предмет исследования — математическое моделирование процесса теплопереноса в ветви хвойного дерева.
При решении дифференциального уравнения в частных производных используется метод конечных разностей (Самарский, Вабищевич, 2003). Хвойная ветвь представляет собой цилиндрическую систему. На ветвь действует фронт пламени лесного пожара. Граничное условие первого рода на границе тела задает значение температуры для каждого момента времени. Для цилиндрической системы уравнение теплопроводности будет иметь вид:
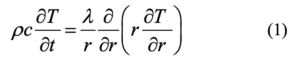
В конечном виде уравнение (1) после аппроксимации частных производных представляется следующим образом:
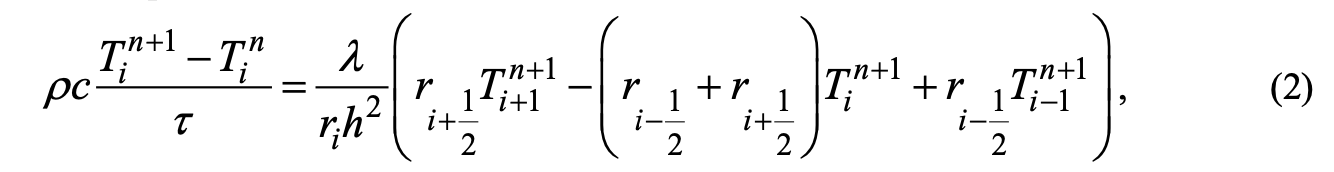
где ρ, c, λ, T — плотность, теплоемкость, теплопроводность и температура материала; r — пространственная координата; t — время; n — номер слоя по времени; i — номер узла по пространственной координате; τ и h — шаги по времени и пространству.
Вычислительные эксперименты проведены с учетом исходных данных, представленных в таблицах 1–4.
Таблица 1. Теплофизические свойства окружающей среды (Grishin, 1997)
| Участок
(рис. 1) |
Название | Характеристика | ||
| ρ, кг/м3 | с, Дж/кг К | λ, Вт/м К | ||
| 4 | зона пламени | 0.656 | 2483 | 0.1836 |
Таблица 2. Теплофизические свойства образцов (Grishin, 1997)
| Сосна | ||||||||
| ρ, кг/м3 | с, Дж/кг К | λ, Вт/м К | ||||||
| сердце-вина | кора | хвоя | сердце-вина | кора | хвоя | сердце-вина | кора | хвоя |
| 500 | 500 | 500 | 1800 | 1670 | 1400 | 0.12 | 0.12 | 0.102 |
| Лиственница | ||||||||
| 660 | 660 | 500 | 2170 | 2170 | 1400 | 0.13 | 0.13 | 0.102 |
| Пихта | ||||||||
| 450 | 450 | 500 | 2700 | 2700 | 1400 | 0.15 | 0.15 | 0.102 |
Таблица 3. Геометрические размеры ветви
| № | Параметр | сердцевина | кора | хвоя |
| 1 | толщина (r, м) | 0.008 | 0.011 | 0.041 |
| 2 | толщина (r, м) | 0.008 | 0.012 | 0.045 |
| 3 | длина (r, м) | 0.008 | 0.013 | 0.049 |
Таблица 4. Диапазон изменений температур в зоне пламени
| Тип ветки | сосна | лиственница | пихта |
| Tf , °C | 800, 900, 1000 | 800, 900, 1000 | 800, 900, 1000 |
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Физическая модель процесса воздействия фронта лесного пожара на ветвь хвойного дерева сформулирована с учетом следующих допущений и предположений.
- Рассматривается одномерная постановка.
- Рассматривается многослойное строение ветви.
- Рассматривается монолитное строение ветви.
- Перенос тепла в системе «ветвь — хвоя — зона пламени» за счет кондукции.
- Теплофизические параметры не зависят от температуры.
- Испарением влаги пренебрегается.
- Пиролизом сухого органического вещества пренебрегается.
- Источник повышения температуры моделируется заданием области повышенной температуры вблизи ветви.
- Рассматривается ситуация, когда источник неподвижен.
Ветвь представляет собой цилиндрическую систему, в состав которой входят сердцевина ветви, корковый слой и слой хвои. Ветвь взаимодействует с зоной пламени. Графическое изображение представлено рисунком 1. Воздействие лесного пожара описывается граничными условиями первого рода.
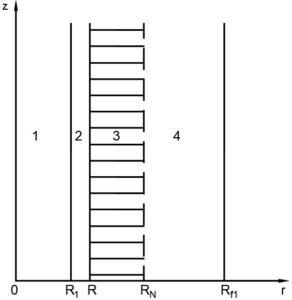
Рисунок 1. Геометрия области решения: 1 — сердцевина, 2 — корковый покров, 3 — хвоя, 4 — зона пламени.
Математически процесс воздействия лесного пожара описывается системой уравнений теплопроводности:
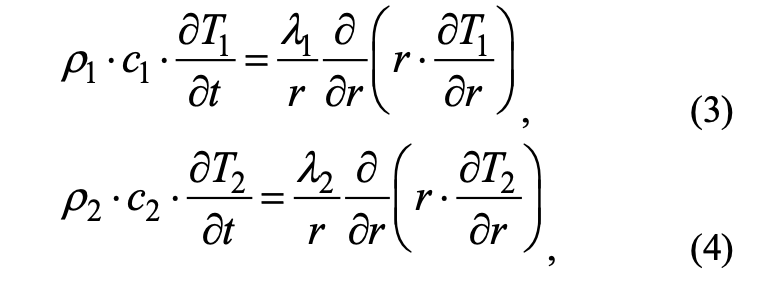
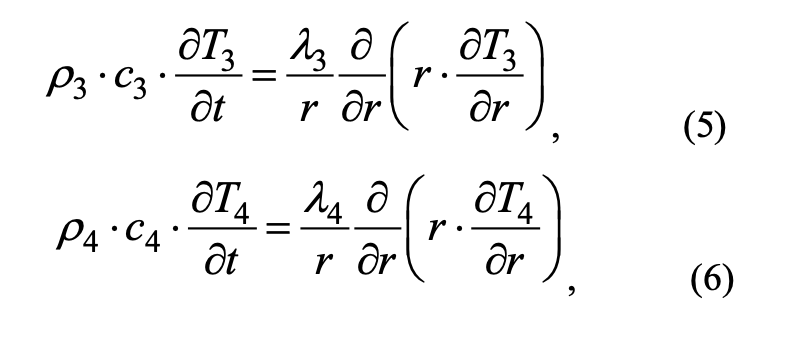
Граничные условия:
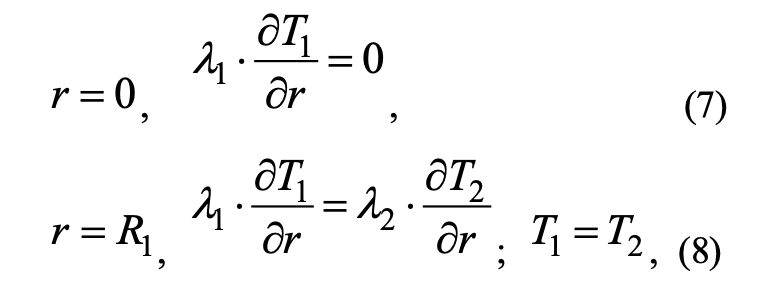
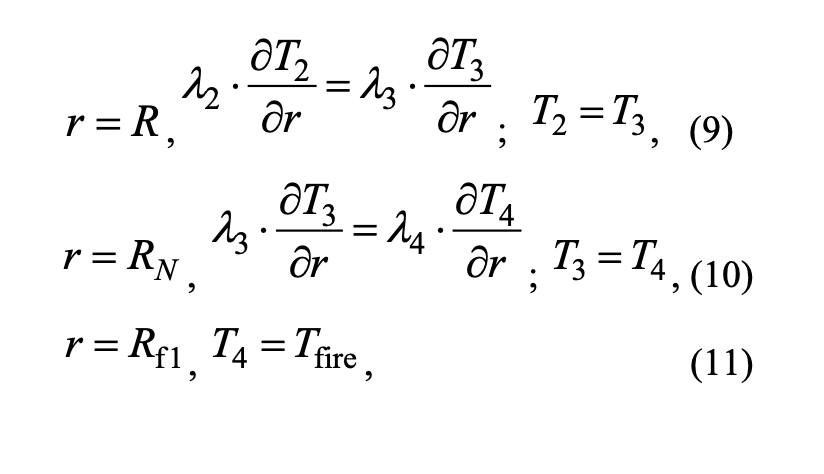
Начальные условия:
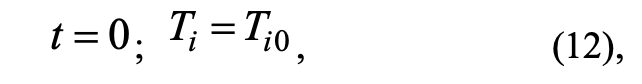
где ρi, сi, Ti, λi — плотность, удельная изобарная теплоемкость, температура, коэффициент теплопроводности (i = 1 — центральной части ветви, i = 2 — коркового покрова ветви, i = 3 — хвои, i = 4 — зоны пламени); Tfire— температура во фронте пожара; t — время; r — пространственная координата; R1 — граница центральной части ветви и коры; R — граница коры и слоя хвои; RN — граница внешнего слоя хвои; Rf1 — граница области решения. Индекс «0» отвечает за параметр в начальный момент времени.
Представленная система уравнений с соответствующими начальными и граничными условиями решена с использованием метода конечных разностей. Конечно-разностные аналоги дифференциальных уравнений решены методом прогонки (Самарский, Вабищевич, 2003).
Процесс теплового воздействия фронта лесного пожара на ветвь хвойного дерева обусловлен переносом тепла за счет кондукции в слоистой структуре ветви. Нагрев осуществляется на внешней границе ветви и математически описывается граничными условиями первого рода, которые моделируют воздействие зоны пламени. Далее тепло передается от более нагретого участка к менее нагретому участку.
По результатам вычислительных экспериментов построены графические зависимости, демонстрирующие распределение температуры в системе «ветвь — хвоя — зона пламени».
На рисунках 2–4 изображены распределения температуры в системе «ветвь — хвоя — зона пламени» для различных сценариев воздействия лесного пожара на ветвь сосны.
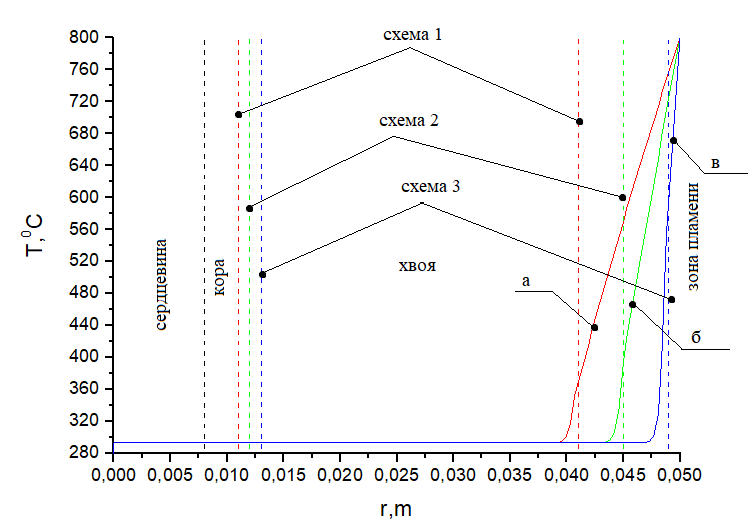
Рисунок 2. Распределение температуры при Тfire = 800 °С на ветвь сосны согласно соответствующим схемам (таблица 3): а) при толщине коры 0.011 м и длине хвои 0.041 м, б) при толщине коры 0.012 м и длине хвои 0.045 м, в) при толщине коры 0.013 м и длине хвои 0.049 м. Время нагрева 1 с
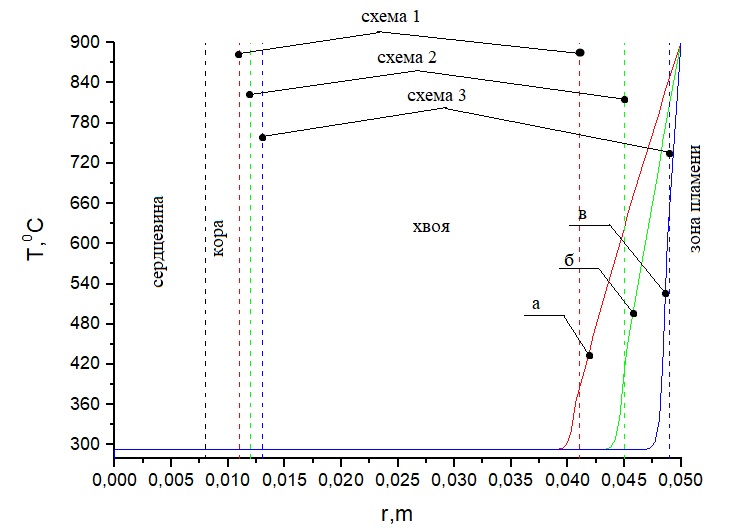
Рисунок 3. Распределение температуры при Тfire = 900 °С на ветвь сосны согласно соответствующим схемам (таблица 3): а) при толщине коры 0,011 м и длине хвои 0.041 м, б) при толщине коры 0.012 м и длине хвои 0.045 м, в) при толщине коры 0.013 м и длине хвои 0.049 м. Время нагрева 1 с
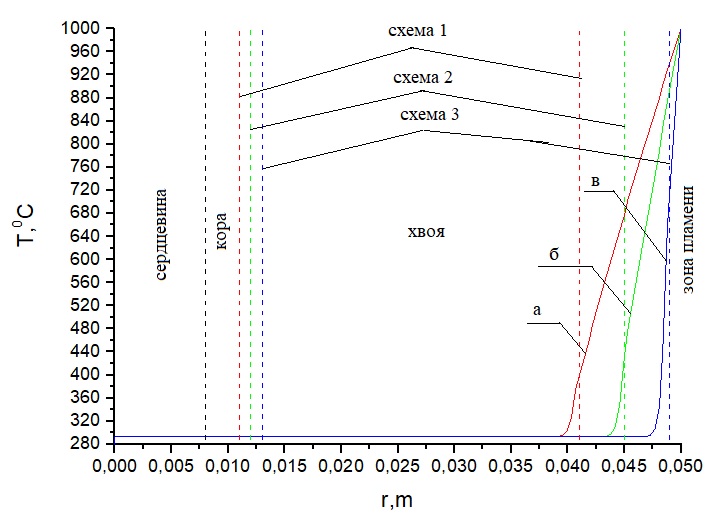
Рисунок 4. Распределение температуры при Тfire = 1000 °С на ветвь сосны согласно соответствующим схемам (таблица 3): а) при толщине коры 0.011 м и длине хвои 0.041 м, б) при толщине коры 0.012 м и длине хвои 0.045 м, в) при толщине коры 0.013 м и длине хвои 0.049 м. Время нагрева 1 с
На рисунках 5–7 изображены распределения температуры в системе «ветвь — хвоя — зона пламени» для различных сценариев воздействия лесного пожара на ветвь лиственницы.
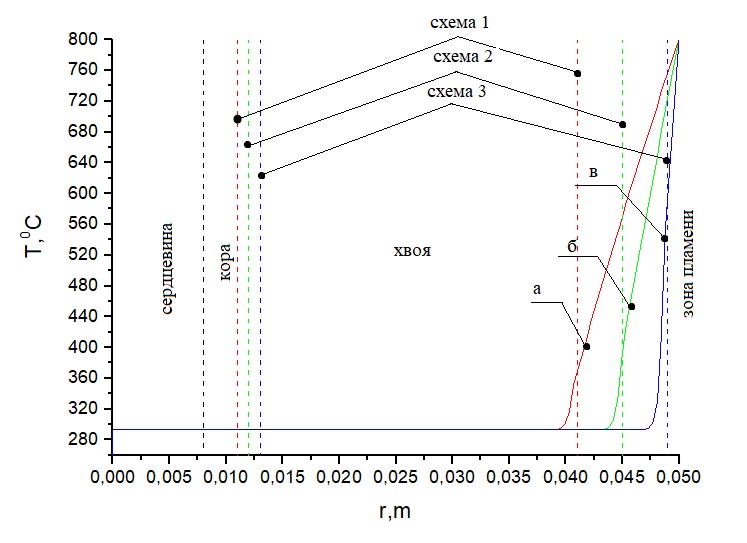
Рисунок 5. Распределение температуры при Тfire = 800 °С на ветвь лиственницы согласно соответствующим схемам (таблица 3): а) при толщине коры 0.011 м и длине хвои 0.041 м, б) при толщине коры 0.012 м и длине хвои 0.045 м, в) при толщине коры 0.013 м и длине хвои 0.049 м. Время нагрева 1 с
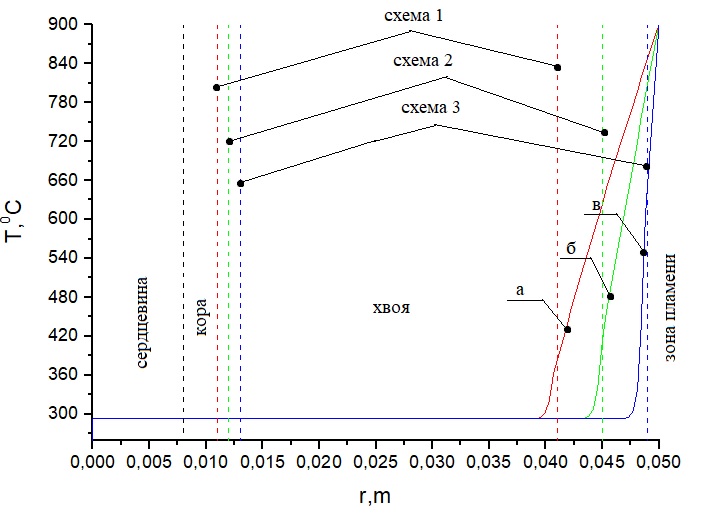
Рисунок 6. Распределение температуры при Тfire = 900 °С на ветвь лиственницы согласно соответствующим схемам (таблица 3): а) при толщине коры 0.011 м и длине хвои 0,041 м, б) при толщине коры 0.012 м и длине хвои 0.045 м, в) при толщине коры 0.013 м и длине хвои 0.049 м. Время нагрева 1 с
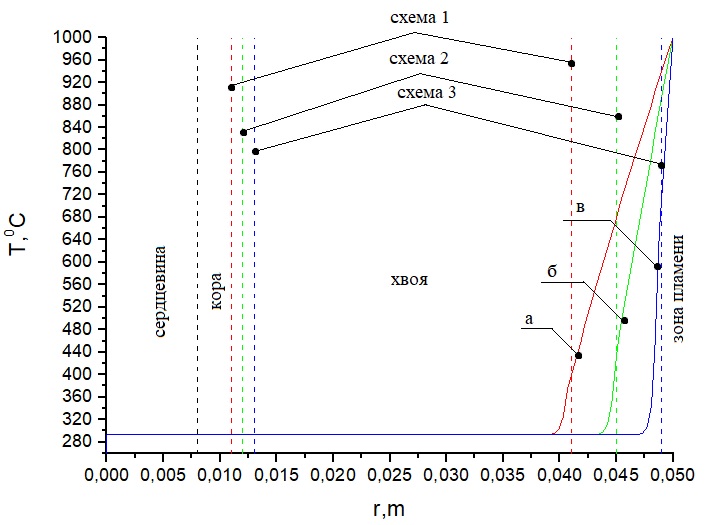
Рисунок 7. Распределение температуры при Тfire = коры 0.011 м и длине хвои 0.041 м, б) при толщине коры 0.012 м и длине хвои 0.045 м, в) при толщине коры 0.013 м и длине хвои 0,.049 м. Время нагрева 1 с
На рисунках 8–10 изображены распределения температуры в системе ««ветвь — хвоя — зона пламени» для различных сценариев воздействия лесного пожара на ветвь пихты.
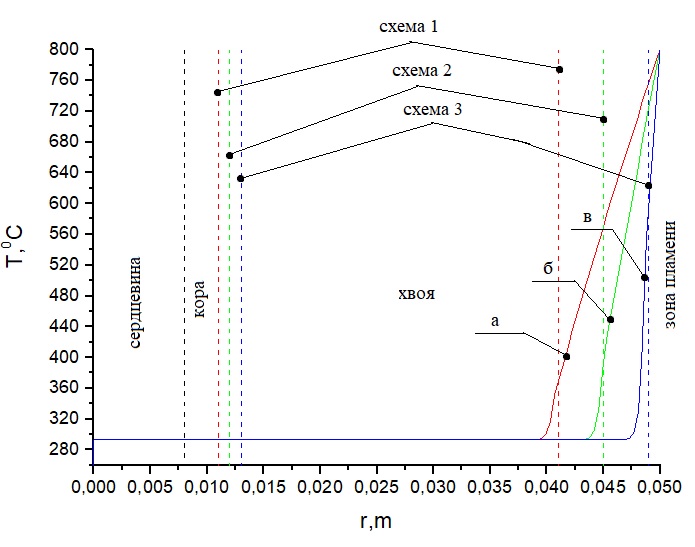
Рисунок 8. Распределение температуры при Тfire = 800 °С на ветвь пихты согласно соответствующим схемам (таблица 3): а) при толщине коры 0.011 м и длине хвои 0.041 м, б) при толщине коры 0.012 м и длине хвои 0.045 м, в) при толщине коры 0.013 м и длине хвои 0.049 м. Время нагрева 1 с

Рисунок 9. Распределение температуры при Тfire = 900 °С на ветвь пихты согласно соответствующим схемам (таблица 3): а) при толщине коры 0.011 м и длине хвои 0.041 м, б) при толщине коры 0.012 м и длине хвои 0.045 м, в) при толщине коры 0.013 м и длине хвои 0.049 м. Время нагрева 1 с
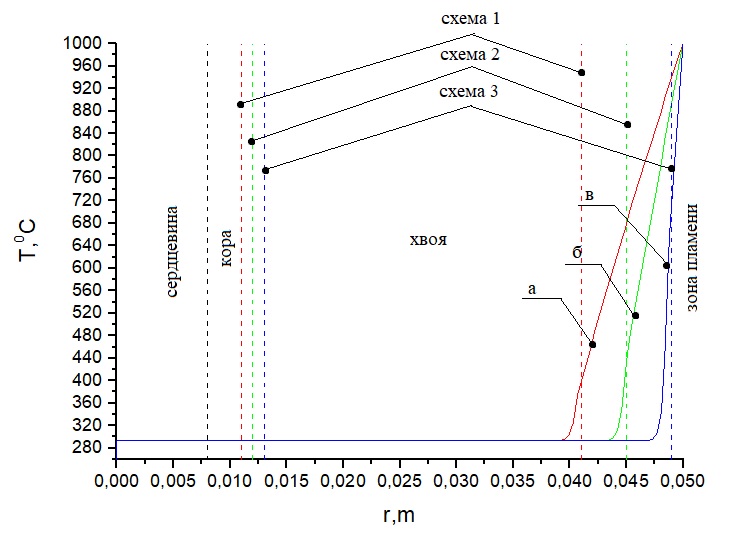
Рисунок 10. Распределение температуры при Тfire = 1000 °С на ветвь пихты согласно соответствующим схемам (таблица 3): а) при толщине коры 0.011 м и длине хвои 0.041 м, б) при толщине коры 0.012 м и длине хвои 0.045 м, в) при толщине коры 0.013 м и длине хвои 0.049 м. Время нагрева 1 с
Анализ температурных зависимостей на рисунках 2–4 показывает, что при всех схемах геометрии области решения наблюдается повышенная температура в верхней части хвоинок за указанный интервал времени воздействия пламени лесного пожара. Чем ближе расположена хвоинка к фронту пламени, тем выше температура на ее окончании. При воздействии низового лесного пожара низкой интенсивности на окончании хвоинки сосны наблюдаются температуры порядка 360 °C для схемы а и 400 °C, 600 °C для схем б и в, в то время как при низовом пожаре высокой интенсивности эти температуры составляют соответственно 390 °C, 460 °C, 660 °C. Верховой лесной пожар приводит к нагреву хвоинок до температур порядка 400 °C, 480 °C, 720 °C. Анализ температурных зависимостей на рисунках 5–7 (лиственница) и рисунках 8–10 (пихта) демонстрирует аналогичные температуры на окончании хвоинок для всех видов рассмотренных лесных пожаров. При температурах до 400 °C происходит интенсивное термическое разложение сухого органического материала хвоинок. При более высокой температуре уже может наблюдаться воспламенение хвоинок, что может привести к необратимым последствиям для отдельно рассматриваемого дерева хвойной породы.
Следует отметить, что сгорание всей хвои и меристемы может вызвать немедленную гибель дерева, если дерево не способно дать ростки из термостойких органов (Clarke et al., 2013; Pausas, Keeley, 2017).
Таким образом, проведено математическое моделирование теплового воздействия от пламени лесного пожара на ветвь хвойного дерева. Рассмотрено три сценария воздействия по типу лесного пожара: низовой пожар низкой интенсивности (800 °C), низовой пожар высокой интенсивности (900 °C) и верховой лесной пожар (1000 °C). Также были исследованы три различные схемы, описывающие различные геометрические строения ветви хвойного дерева. Понятно, что это приближенные данные и в реальной ситуации геометрия ветви может значительно различаться от породы дерева, вегетационного периода и возраста дерева, а также его физиологического состояния. Использование только теплофизической модели для исследования теплопереноса в ветви хвойного дерева показало, что температурные распределения для различных пород достаточно схожи. А значит, необходима дальнейшая модернизация настоящей математической модели. Так, необходимо учесть испарение влаги и термическое разложение сухого органического вещества. Кроме того, в последующих исследованиях следует учесть данные по физиологической активности различных пород и экспериментальные данные по отмиранию тканей дерева при различных температурах. То есть необходимо дополнить разработанную математическую модель критериями поражения тканей ветви в зависимости от температуры во фронте лесного пожара и продолжительности воздействия. Еще одним направлением усовершенствования математической модели может стать учет конвективного и лучистого теплообмена на внешней границе ветви, непосредственно подверженной воздействию поражающих факторов лесного пожара. В перспективе такая математическая модель может быть использована в качестве основы для создания программных инструментов в специализированных геоинформационных системах мониторинга состояния лесных массивов и прогнозирования их функционирования в послепожарный период.
ЗАКЛЮЧЕНИЕ
Таким образом, в результате проведенного исследования разработана базовая математическая модель теплопереноса в слоистой структуре ветви хвойного дерева на основе нестационарных дифференциальных уравнений теплопроводности с соответствующими начальными и граничными условиями. Предварительный анализ полученных результатов показывает, что использование только наработок в области тепломассопереноса не дает четкого ответа на вопросы касательно образования термических поражений в ветви различных хвойных пород. Необходимо интегрировать в математическую модель количественные и качественные критерии образования термических поражений, разработанные на основе анализа физиологических процессов и экспериментов по воздействию повышенной температуры на ткани дерева.
БЛАГОДАРНОСТИ
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований. Научный проект № 17-29-05093.
СПИСОК ЛИТЕРАТУРЫ
Лесотека. Режим доступа: https://lesoteka.com/ (дата обращения 17 февраля 2021 г.).
Самарский А. А., Вабищевич П. Н. Вычислительная теплопередача. М.: Эдиториал УРСС, 2003. 784 с.
Шилов И. А. Экология. М.: Высшая школа. 2003. 512 с.
Bar A., Michaletz S. T., Mayr S. Fire effects on tree physiology // New Phytologist. 2019. Vol. 223. P. 1728–1741.
Baranovskiy N. V. Predicting, Monitoring, and Assessing Forest Fire Dangers and Risks. IGI Global. 2020. 477 p.
Baranovskiy N. V., Kuznetsov G. V. Forest fire occurrences and ecological impact prediction: monograph. Novosibirsk: Publishing House of the Siberian Branch of the Russian Academy of Science, 2017. 259 p.
Battipaglia G., Strumia S., Esposito A., Giuditta E., Sirignano C., Altieri S., Rutigliano F. A. The effects of prescribed burning on Pinus halepensis Mill. As revealed by dendrochronological and isotopic analysis // Forest Ecology and Management. 2014. Vol. 334. P. 201–208.
Bergman T. L., Incropera F. P. Fundamentals of heat and mass transfer. Hoboken, NJ, USA: John Wiley & Sons, 2011.
Clarke P. J., Lawes M. J., Midgley J. J., Lamont B. B., Ojeda F., Burrows G. E., Enright N. J., Knox K. J. E. Resprouting as a key functional trait: How buds, protection and resources drive persistence after fire // New Phytologist. 2013. Vol. 197. P. 19–35.
Dickinson M. B., Johnson E. A. Temperature-dependent rate models of vascular cambium cell mortality // Canadian Journal of Forest Research. 2004. Vol. 559. P. 546–559.
Grishin A. M. Mathematical modeling of forest fire and new methods of fighting them. Russia. Tomsk: Publishing House of the Tomsk State University, 1997. 390 р.
Hare R. C. Heat effects on living plants. Occasional Paper 183. New Orleans, LA, USA: USDA Forest Service, Southern Forest Experiment Station. 1961.
Lambert B. S., Stohlgren T. J. Giant sequoia mortality in burned and unburned stands // Journal of Forestry. 1988. Vol. 86. P. 44–46.
Van Mantgem P., Schwartz M. Bark heat resistance of small trees in Californian mixed conifer forests: testing some model assumptions // Forest Ecology and Management. 2003. Vol. 178. P. 341–352.
Van Mantgem P., Stephenson N. L., Knapp E., Battles J., Keeley J. E. Long-term effects of prescribed fire on mixed conifer structure in the Sierra Nevada, California // Forest Ecology and Management. 2011. Vol. 261. P. 989–994.
Michaletz S. T., Johnson E. A. A heat transfer model of crown scorch in forest fires // Canadian Journal of Forest Research. 2006. Vol. 36. P. 2839–2851.
Michaletz S. T., Johnson E. A. How forest fires kill trees: a review of the fundamental biophysical processes // Scandinavian Journal of forest research. 2007. Vol. 22. P. 500–515.
Michaletz S. T., Johnson E. A., Mell W. E., Greene D. F. Timing of fire relative to seed development may enable non-serotinous species to recolonize from the aerial seed banks of fire-killed trees // Biogeosciences. 2013. Vol. 10. P. 5061–5078.
O’Brien J. J., Hiers J. K., Varner J. M., Hoffman C. M., Dickinson M. B., Michaletz S. T., Loudermilk E. L., Butler B. W. Advances in mechanistic approaches to quantifying biophysical fire effects // Current Forestry Reports. 2018. Vol. 4. P. 161–177.
Pausas J. G., Keeley J. E. Epicormic resprouting in fire-prone ecosystems // Trends in Plant Science. 2017. Vol. 22. P. 1008–1015.
Pounden E., Greene D. F., Michaletz S. T. Non-serotinous woody plants behave as aerial seed bank species when a late-summer wildfire coincides with a mast year // Ecology and Evolution. 2014. Vol. 4. P. 3830–3840.
Pearson H. A., Davis J. R., Schubert G. H. Effects of wildfire on timber and forage production in Arizona // Journal of Range Management. 1972. Vol. 25. P. 250–253.
Rosenberg B., Kemeny G., Switzer R. C., Hamilton T. C. Quantitative evidence for protein denaturation as the cause of thermal death // Nature. 1971. Vol. 232. P. 471–473.
Thompson M. T. C., Koyama A., Kavanagh K. L. Wildfire effects on physiological properties in conifers of central Idaho forests, USA // Trees. 2017. Vol. 31. P. 545–555.
Valor T., Casals P., Altieri S., Gonzalez-Olabarria J. R., Pique M., Battipaglia G. Disentangling the effects of crown scorch and competition release on the physiological and growth response of Pinus halepensis Mill. Using δ13C and δ18O isotopes // Forest Ecology and Management. 2018. Vol. 424. P. 276–287.
Van Wagner C. E. Height of crown scorch in forest fires // Canadian Journal of Forest Research. 1973. Vol. 3. P. 373–378.
Yakimov N., Ponomarev E. Dynamics of post-fire effects in larch forests of Central Siberia based on Satellite data // E3S Web of Conference. 2020. Vol. 149. Article Nо. 03008.
Рецензент: к. т. н. доцент Гоман П. Н.





