- DOI: 10.31509/2658-607x-202582-170
- УДК 595.2: 537.017: 574.472
Моделирование динамики численности видов в сообществах коллембол
© 2025 В. Г. Суховольский1*, Н. А. Кузнецова2, А. В. Ковалев3
1Центр по проблемам экологии и продуктивности лесов им. А. С. Исаева РАН
Россия, 117997 Москва, ул. Профсоюзная, 84/32, стр. 14
2Московский государственный педагогический университет
Россия, 119435 Москва, ул. Малая Пироговская, дом 1, строение 1
3Федеральный исследовательский центр КНЦ СО РАН,
Россия, 660036 Красноярск, Академгородок, 50
*E-mail: soukhovolsky@yandex.ru
Поступила в редакцию: 20.05.2025
После рецензирования: 16.06.2025
Принята к печати: 19.06.2025
Рассмотрена динамика численности коллембол на материале долгосрочных учетов. Для анализа использовались данные о суммарных плотностях популяций коллембол трех функциональных групп. Группа коллембол S объединяет эу- и гемиэдафические формы, населяющие подстилку и нижележащие горизонты почвы. Группа коллембол U включает верхнеподстилочные формы, обитающие на поверхности подстилки. Группа А состоит из атмобионтных коллембол, поднимающихся в напочвенный растительный покров. Для временных рядов динамики численности коллембол каждой группы были рассмотрены ADL (autoregressive distributed lag)-модели, в которых текущая численность коллембол определялась как зависящая, во-первых, от регулирующих факторов – численности коллембол в три предыдущих учета, и, во-вторых, от модифицирующего фактора – накопленной температуры воздуха в течение трех недель до даты учета. Предложенная модель позволила достаточно точно (коэффициенты детерминации R2 для всех групп превосходили 0.7) описать многолетнюю динамику численности коллембол трех функциональных групп. Для оценки устойчивости динамики численности коллембол был вычислен такой показатель, как запас по устойчивости ADL-модели и показано, что динамики численности коллембол достаточно стабильна и превосходит показатели запаса по устойчивости популяций лесных насекомых.
Ключевые слова: почвенная мезофауна, почва, подстилка, многолетний мониторинг
Почвенные животные, наряду с микроорганизмами, участвуют в процессах разложения растительных остатков, поддерживая естественное плодородие почвы и ее экосистемные функции. Среди мелких почвенных членистоногих особенно многочисленны и разнообразны коллемболы (Collembola), или ногохвостки – всесветно распространенные древнейшие обитатели суши. Группа известна своей чувствительностью к внешним факторам среды и нередко используется в экологическом мониторинге. Было обнаружено сокращение разнообразия коллембол и сдвиги структуры их сообществ, что связывают с глобальным потеплением (Jucevica, Melecis, 2006; Bokhorst et al., 2012; Potapov et al., 2020). Это тревожное явление требует всестороннего изучения. В особенности важно оценить закономерности динамики численности видов этой группы.
Проблема анализа закономерностей динамики численности близких по своим экологическим характеристикам видов животных, возможно, конкурирующих за один общий или несколько сопряженных ресурсов – одна из старейших в экологии, начиная с работ А. Лотки и В. Вольтерра (Lotka, 1925; Volterra, 1926; Свирежев, Логофет, 1978; Колесов, 1981; Марри, 1983; Базыкин, 1983, 2003; Исаев и др., 2001, 2015; Keith, 1963; Odum, Barrett, 1971; Gomatam, 1974; Berryman, 1981, 2003; Britton, 2003). В базовой модели динамики численности конкурирующих видов рассматриваются системы дифференциальных или разностных уравнений, члены в которых описывают как собственную динамику роста отдельного видов, так и взаимодействие между конкурирующими видами (Вольтерра, 1976). Однако для большого по числу видов сообщества решение таких уравнений затруднительно в связи с отсутствием достаточно длинных рядов динамики численности. Это связано со сложностью и трудоемкостью учетов на одной и той же пробной площади в течение многих лет, а также со сложностью нахождения решений систем нелинейных уравнений динамики, отсутствием информации о характере парных взаимодействиях видов в сообществе и трудностью включения в модель влияния модифицирующих факторов, таких, как погодные. По этой причине при изучении сложных сообществ предпочитают использовать не системы уравнений динамики, а вводят различные интегральные характеристики, такие, как индексы видового обилия и разнообразия в сообществах (Hutchinson, 1947; Whittaker, 1965; Мэгарран, 1992; Суховольский, 2004; McGill et al., 2007; Пузаченко, 2016; Левич, 2007; Levich et al., 2009; Matthews, Whittaker, 2015). Такой подход позволяет снять проблемы расчетов характеристик временной динамики видов в сообществе, однако затрудняет анализ взаимодействия видов.
При анализе экологических процессов и динамики численности в сообществах животных существует проблема выбора оптимального объекта для исследования. Для получения информации о состоянии сообществ важно выбрать для анализа достаточно многочисленные сообщества, но при этом иметь возможность измерения численностей всех популяций в сообществе.
Верификация моделей взаимодействующих популяций (начиная с работы Г. Гаузе (Gause, 1934), связана с необходимостью знания данных по динамике численности взаимодействующих видов. Трудности моделирования численности взаимодействующих видов в экосистеме можно разделить на системные и процессные. Системные ограничения связаны с тем, что в связи с техническими трудностями учетов всех взаимодействующих популяций в изучаемой системе ведутся учеты лишь части этих видов. Процессное ограничение возникает вследствие того, что по техническим и экономическим причинам наблюдения за популяциями в экосистеме имеются лишь в короткий интервал времени. В связи с этими трудностями для построения моделей взаимодействующих популяций используется ограниченное число длительных сопряженных рядов популяций хищников и жертв, в частности, очень популярные при построении моделей «хищник – жертва» многолетние данные по закупке шкурок зайцев (Lepus americanus) и рысей (Lynx lynx) Компанией Гудзонова залива (Hewitt, 1921; Elton, Nicholson, 1942; Gilpin, 1973; Bulmer, 1974; Stenseth еt al., 1997; Zhang et al., 2007; Deng, 2018).
Популяцию любого вида животных можно рассматривать как авторегулируемую систему с обратными связями (в частности, для лесных насекомых такой подход успешно рассматривался в ряду исследований (Исаев, Хлебопрос, 1973; Berryman, 1981; Исаев и др., 2001; Isaev et al., 2017). Такая общая модель может быть описана через, так называемую «передаточную функцию» с обратными связями разной силы и направленности и с разным запаздыванием во времени (Дорф, Бишоп, 2004). При этом при анализе общих свойств временной динамики популяций животных регулирующие факторы, оказывающих влияние на конкретную популяцию, можно не рассматривать и достаточно оценить восприимчивость популяции к влиянию обратных связей и запаздывание отклика системы на ее состояние на входе (Royama, 1992; Turchin, 1990). Если задача состоит в построении модели вида жертвы, для верификации такой модели не требуются данные о численности хищников (сколько бы видов хищников ни воздействовало на популяцию жертвы – рысь, трапперы, волк, росомаха, рыжая лисица, большая рогатая сова, обыкновенная сова и др. (Rohner,1996; Stenseth et al., 1997).
Одним из экологических объектов, пригодных для такого анализа, являются сообщества коллембол (Collembola) – почвенных членистоногих. Различные виды этих членистоногих населяют подстилку и верхние горизонты почв. Коллемболы способствуют разложению, превращению в гумус и минерализации растительных остатков и играют очень важную роль в почвообразовании (Hopkin, 1997; Hassall et al., 2006; Maaß et al., 2015). В почвах любых типов всегда присутствуют коллемболы (Petersen, Luxton, 1982; Potapov et al., 2023), которые возможно использовать для изучения закономерностей сложения структуры сообществ (Кузнецова, 2008). Учеты коллембол в почвах достаточно просты технически (Гиляров, 1975; Потапов, Кузнецова, 2011) и позволяют получить многолетние данные о численности различных видов коллембол. Анализ характеристик видового состава коллембол потенциально может дать информацию о процессах, происходящих в биоте. Можно ожидать, что при поддержании на стационарном уровне состояния почвы будет наблюдаться стационарная динамика численности отдельных видов коллембол, поддерживаться постоянной структура сообщества коллембол, а при внешних воздействиях на почву или ее деградации будут происходить изменения этих характеристик.
Однако влияние эндогенных и экзогенных факторов на сообщества коллембол будет приводить к возникновению колебаний плотности популяции коллембол, изменений видовой структуры сообщества и пространственной структуры распределения особей на пробных площадях. Поэтому для оценки состояния сообщества коллембол необходимо либо отделить изменения характеристик коллембол вследствие изменения состояния почвы и внешних воздействий на нее от собственной эндогенной динамики в стационарной среде (что достаточно сложно), либо ввести некоторые интегральные инвариантные во времени характеристики структуры всего сообщества.
Настоящая работа посвящена анализу динамики численности сообщества коллембол и в ней рассматривается возможность построения интегральной модели многолетней динамики численности отдельных групп видов коллембол с малым числом управляющих параметров.
ОБЪЕКТЫ И МЕТОДЫ ИССЛЕДОВАНИЯ
Исследования проведены в Московской области, расположенной в полосе хвойно-широколиственных лесов, в Наро-Фоминском р-не (с 2012 г. это территория Новой Москвы) на биогеоценологическом стационаре «Малинки» ИПЭЭ РАН им. А. Н. Северцова. Пробная площадь (N55.4581, E37.1768) находилась в ельнике-кисличнике (Piceetum oxalidosum) с примесью сосны. Сомкнутость крон – 0.8. Средний возраст древостоя к концу исследования – 120 лет. В напочвенном покрове доминирует кислица обыкновенная, – проективное покрытие около 70%. Многочисленны живучка ползучая, майник двулистный, земляника, зеленые мхи. Мощность подстилки варьирует от 1 до 5 см. Почва – подзолистая (Классификация …, 1997).
Пробы отбирали буром с площадью сечения 8 см2 на всю глубину подстилки и гумусового горизонта, захватывая 1-2 см нижележащего минерального горизонта почвы без разделения на горизонты. Пробы располагали в линию между деревьями: около стволов (2 пробы), под кронами (2 пробы) и в «окне»[1] – пространстве между деревьями (1 проба) (Kuznetsova, 2006). За один учет отбирали пробы с 4-х таких линий, всего 20 проб. Учеты проводили с 1991 по 1999 гг. со средней периодичностью 7 раз в год.
Для экстракции коллембол использовали воронки Тульгрена с фиксацией в 70% этаноле. Все особи заключали в микропрепараты и определяли под микроскопом. Всего собран и определен 25551 экземпляр ногохвосток 54 видов (Kuznetsova, 2007).
Коллемболы населяют различные ярусы биогеоценозов: почву, включая подстилку, ее поверхность и напочвенный покров. Соответственно этим компонентам виды были разделены на три функциональные группы для моделирования динамики численности. Для анализа использовали данные о суммарной плотности популяций коллембол этих групп, связанных с жизненными формами по С. К. Стебаевой (1970) следующим образом. Группа коллембол S (от soil) объединяет эу- и гемиэдафические формы, населяющие различные горизонты почв, включая подстилку. Коллемболы в группе U (от upper litter) включают только верхнеподстилочные формы, обитающие на поверхности подстилки. Группа А (от atmobios) состоит из атмобионтных коллембол, поднимающихся в напочвенный покров, а также нейстонные и кортицикольные формы. Для периода с 1991 по 1999 г. были рассмотрены временные ряды суммарных численностей видов в группах коллембол: A, S, U. При этом особи одного вида могут встречаться в разных почвенных горизонтах. Перечень видов коллембол, входящих в каждую из этих групп, приведен Приложении.
Методы анализа данных
Обычно при построении моделей динамики численности используют данные о плотности (численности) популяции через заданный интервал времени (например, 1 год). Однако при анализе динамики численности коллембол по техническим причинам это условие не выполнялось. В среднем учеты проводились с периодичность раз в 49 дней (зимой проведено 4 учета). Тем не менее, приближенно можно моделировать динамику численности, используя вместо даты учета его номер k, что позволяет построить равномерный аналог временной шкалы.
Высокочастотные колебания в ряду динамики численности связаны как с ошибками учетов, так и влиянием быстрых изменений состояния природной среды. Эти процессы не оказывают сильного влияния на многолетние изменения динамики численности и для упрощения моделей от этих колебаний желательно избавиться. Для этого для каждого ряда n(i) проводилось фильтрация высокочастотной составляющей с помощью фильтра Ханна (Хемминг, 1987):
y(i) = 0.24n(i-1)+0.52n(i)+0.24n(i+1) (1),
позволяющего убрать составляющие с частотами выше 0.25 при расчетах с использованием в качестве максимального значения в спектре частоты Найквиста f = 0.5 – интервала времени между измерениями, принимаемого за единицу отсчета (Дженкинс, Ваттс, 1971, с. 71), характеризующие случайные колебания численностей в ходе учета.
Далее для ряда оценивалось наличие временного тренда. Если такой тренд не регистрировался, производилась оценка их авторегрессионных свойств ряда – зависимости текущего значения ряда y(i) от k предыдущих значений – порядок авторегрссии. Для оценки порядка k авторегрессии вычислялась парциальная автокорреляционная функция (ПАКФ) (Дженкинс, Ваттс, 1971). Порядок авторегрессии соответствовал числу членов ПАКФ, больших по модулю стандартной ошибки sy.
Авторегрессионное (AR) уравнение порядка r для логарифма численности коллембол в i-ом учете запишем следующим образом: 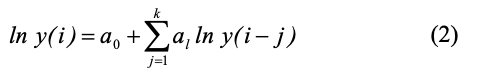
В уравнении (2) значения ln известны и это уравнение можно рассматривать как линейное регрессионное уравнение относительно неизвестных параметров a0 — as. Можно также рассмотреть более сложное ADL (autoregressive distributed lag)-уравнение, в котором дополнительно учитывается влияние погодных условий: 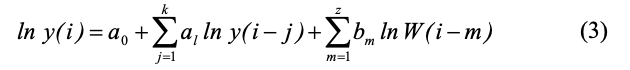
где W(i) – погодная характеристика: сумма температур воздуха за некоторое время до момента i.
В наших расчетах в качестве оптимальной погодной характеристики, при выборе которой значение коэффициента детерминации уравнения (3) было максимальным, использовалась величина логарифма суммы температур за три недели до учета.
Для оценки порядка авторегрессии ряда длиной n вычислялась парциальная автокорреляционная функция (ПАКФ) и ее стандартные ошибки ![]() . За порядок авторегрессии принимался наибольший номер члена ПАКФ, значение ПАКФ которого превосходило по модулю стандартную ошибку.
. За порядок авторегрессии принимался наибольший номер члена ПАКФ, значение ПАКФ которого превосходило по модулю стандартную ошибку.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
На рисунке 1 приведена ПАКФ временного ряда коллембол группы U в 1991–1999 гг.

Рисунок 1. Парциальная автокорреляционная функция (ПАКФ) временного ряда суммарного числа коллембол группы U* в 1991–1999 гг. 1 – ПАКФ, 2 – стандартные ошибки ПАКФ. Примечание: *Здесь и далее обозначение групп коллембол (U, S, A) См. раздел «Объекты и методы исследования»
Как видно из рисунка 1, порядок авторегрессии равен 3, поэтому ADL-модель должна иметь следующий вид: 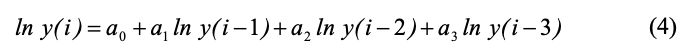
Если в качестве внешнего модифицирующего фактора выбрать логарифм накопленной сумму температур за три недели до проведения учетов ln W(i), то вместо уравнения (4) будем использовать ADL-модель: 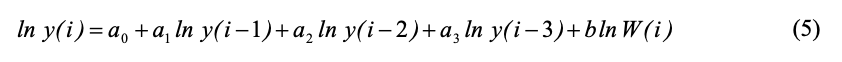
Так как значения ln y(i) известны для всех i, то уравнение (5) можно рассматривать как линейное регрессионное уравнение относительно неизвестных величин а0 – а3 и b. Эти параметры (5) можно вычислить стандартными методами решения регрессионных уравнений.
В таблице 1 приведены значения коэффициентов а0 – а3 и b регрессионного уравнения (5) для временного ряда коллембол группы U.
Таблица 1. Характеристики регрессионного уравнения (5) для временного ряда коллембол группы U
| Переменные
/коэффициенты |
Значения коэффициентов | Стандартная ошибка | t-критерий | Уровень достоверности p |
| /a0 | -39.30 | 11.82 | -3.32 | 0.001619 |
| ln W(i)/b | 4.652 | 1.377 | 3.38 | 0.001385 |
| ln y(i-3)/a3 | 0.256 | 0.133 | 1.93 | 0.059542 |
| ln y(i-2)/a2 | -0.860 | 0.1615 | -5.32 | 0.000002 |
| ln y(i-1)/a1 | 0.998 | 0.145 | 6.88 | 0.000000 |
| Adjusted R2 | 0.720 | |||
| F-критерий | 34.01 | |||
| Запас по устойчивости h | 0.326 |
На рисунке 2 приведены ряд учетов (кривая 1) и модельный временной ряд (кривая 2).

Рисунок 2. Ряд учетов коллембол группы U (кривая 1) и модельный временной ряд (кривая 2)
Для оценки синхронности динамики ряда наблюдений и модельного ряда вычислялась кросс-корреляционная функция (ККФ) (рис. 3). Если при сдвиге k =0 значение ККФ близко к 1, это указывает на синхронность во времени временного ряда наблюдений и модельного временного ряда.

Рисунок 3. Кросс-корреляционная функция (ККФ) ряда данных наблюдений и модельного ряда коллембол группы U. 1 – ККФ; 2 – стандартные ошибки ККФ
Наличие колебаний ККФ указывает на существование циклических колебаний в ряде наблюдений. Для расчета циклических процессов вычислялась спектральная плотность ряда наблюдений (рис. 4). Для расчетов частоты используется частота Найквиста с максимальным значением f = 0.5.

Рисунок 4. Спектральная плотность ряда учетов коллембол группы U; – средний интервал времени между смежными учетами (≈ 40 дней). f = 0.5 – частота Найквиста
Как видно из рисунка 4, данные учетов характеризуются циклической составляющей с периодом около одного года. По всей видимости, такая периодичность связана со снижением численности в зимний период и ее восстановлением весной.
Аналогичные расчеты были выполнены для временных рядов численностей коллембол групп S и A. Для этих временных рядов порядок авторегрессий также был равен 3. В таблицах 2 и 3 приведены расчеты параметров ADL-модели временной динамики коллембол групп S и A, на рисунках 5–8 – соответственно наблюдаемые и модельный временные ряды и спектр временного ряда коллембол слоев S и A.
Таблица 2. Характеристики регрессионного уравнения (5) для временного ряда коллембол группы S
| Переменные
/коэффициенты |
Значения коэффициентов | Стандартная ошибка | t-критерий | Уровень достоверности p |
| /a0 | -22.605 | 7.504 | -3.012 | 0.003969 |
| ln W(i)/b | 2.662 | 0.860 | 3.096 | 0.003129 |
| ln y(i-3)/a3 | 0.228 | 0.127 | 1.803 | 0.077152 |
| ln y(i-2)/a2 | -0.838 | 0.198 | -4.227 | 0.000094 |
| ln y(i-1)/a1 | 1.438 | 0.123 | 11.702 | 0.000000 |
| Adjusted R2 | 0.85 | |||
| F-критерий | 74.00 | |||
| Запас по устойчивости h | 0.172 |
Таблица 3. Характеристики регрессионного уравнения (5) для временного ряда коллембол группы А
| Переменные
/коэффициенты |
Значения коэффициентов | Стандартная ошибка | t-критерий | Уровень достоверности p |
| /a0 | -30.376 | 10.723 | -2.833 | 0.006513 |
| ln W(i)/b | 3.557 | 1.234 | 2.881 | 0.005704 |
| ln y(i-3)/a3 | 0.435 | 0.115 | 3.799 | 0.000376 |
| ln y(i-2)/a2 | -1.045 | 0.174 | -6.006 | 0.000000 |
| ln y(i-1)/a1 | 1.357 | 0.129 | 10.484 | 0.000000 |
| Adjusted R2 | 0.83 | |||
| F-критерий | 63.01 | |||
| Запас по устойчивости h | 0.253 |

Рисунок 5. Сглаженный временной ряд учетов коллембол группы S (1) и модельный временной ряд (2)

Рисунок 6. Спектральная плотность временного ряда учетов коллембол группы S; – средний интервал времени между смежными учетами (≈ 40 дней). f = 0.5 – частота Найквиста

Рисунок 7. Ряд учетов коллембол группы А (1) и модельный временной ряд (2)

Рисунок 8. Спектральная плотность временного ряда учетов коллембол группы А; – средний интервал времени между смежными учетами (≈ 40 дней), f = 0.5 – частота Найквиста
Важной характеристикой динамики численности коллембол разных функциональных групп является их временная сопряженность, оцениваемая с помощью ККФ пар временных рядов групп A, S, U.
Если временные ряды синхронны, то максимум ККФ наблюдается при сдвиге k=0. Если ряды сдвинуты по фазе, то максимум ККФ наблюдается при значении k, отличном от нуля. На рисунках 9–11 приведены ККФ пар рядов коллембол групп A, S, U.

Рисунок 9. Кросс-корреляционная функция (ККФ) рядов коллембол групп А и S. 1 – ККФ; 2 – стандартные ошибки ККФ

Рисунок 10. Кросс-корреляционная функция (ККФ) временных рядов коллембол групп А и U. 1 – ККФ; 2 – стандартные ошибки ККФ

Рисунок 11. Кросс-корреляционная функция (ККФ) рядов коллембол групп S и U. 1 – ККФ; 2 – стандартные ошибки ККФ
Как видно из рисунков 9–11, временные ряды групп A, S, U не синхронны и между ними наблюдаются фазовые сдвиги.
С чем может быть связан сдвиг по фазе во временной динамике численности коллембол разных функциональных групп? Можно рассмотреть различные причины, например, связь плотности популяции коллембол с влажностью почвы. Как известно, вода в глубинные слои почвы медленнее проникает и дольше сохраняется. Но для проверки этой гипотезы необходимы сопряженные измерения численности коллембол и влажности почвенного слоя. Но при проведении таких экспериментов нужно помнить о возможном запаздывании популяционной динамики по сравнению с динамикой влажности и связи между изменением численности коллембол и влажности почвы необходимо рассматривать в рамках интегрального уравнения 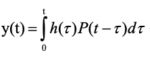 (где P(t) – влажность почвенного слоя, h(τ) – ядро интегрального уравнение, характеризующее реакцию коллембол на изменения влажности.
(где P(t) – влажность почвенного слоя, h(τ) – ядро интегрального уравнение, характеризующее реакцию коллембол на изменения влажности.
Для AR-моделей популяционной динамики важной характеристикой, позволяющей оценить изменение состояние популяции при различного рода трансформациях внешней среды и собственных характеристик популяции, являются запас модели по устойчивости. Величина запаса по устойчивости характеризует близость этой точки к границам зоны устойчивости. Для оценки запаса устойчивости дискретных систем используется критерий Михайлова и годограф Михайлова (Ким, 2007).
Несмотря на внешне сложную процедура расчета, расчет запаса по устойчивости выполняется с помощью простой программы (табл. 4) в пакете MATLAB.
Таблица 4. Листинг программы в пакете MATLAB для расчета запаса по устойчивости авторегрессионной модели (Гайдук и др., 2011):
| Dq = [1 a[1] a[2] a[3]; |
| Dq = Dq/Dq(1); |
| nu = (-pi: pi/(100*length(Dq)):pi; |
| j = sqrt(-1); |
| z = exp(j*nu); |
| GM = polyval (Dq, q); |
| eta = min (abs(GM)); |
| disp ([‘запас устойчивости eta =‘ num2str(eta)]) |
Для расчета запаса по устойчивости необходимо в пакете MATLAB загрузить программу из таблицы 3 и выполнить лишь одну операцию: ввести в строку 1 значения коэффициентов авторегрессионной модели. По определению величина запаса по устойчивости и чем меньше значение h, тем больше вероятность «срыва» и потери устойчивости системы при внешних воздействиях.
Показатели запаса по устойчивости для рассмотренных популяций коллембол трех функциональных групп приведены в таблицах 1, 2 и 3. Как видно, запас по устойчивости для популяций коллембол группы U составляет 0.326, для коллембол группы S h = 0.172, для коллембол группы А h = 0.256. Заметим, что для популяций лесных насекомых с сильными колебаниями численности этих видов величины запаса по устойчивости не превосходят h = 0.12. Найденные значения запаса по устойчивости для коллембол указывают на достаточную стабильность динамики их сообществ.
Предложенная модель достаточно точно (коэффициенты детeрминации R2>0.70 позволяет описать динамику численности трех функциональных групп коллембол. При этом наблюдаемый и модельный ряды синхронны, максимумы и минимумы логарифмов численностей согласуются. Динамика численности каждой группы характеризуется наличием памяти, и текущая численность зависит от численностей в трех предыдущих значениях. Подобные расчеты ранее были выполнены для популяций лесных насекомых и было показано, что для видов из этой таксономической группы характерно запаздывание k = 2 (Soukhovolsky et al., 2025), то есть регуляция в популяциях лесных насекомых несколько быстрее, чем в популяциях почвенных членистоногих. Коэффициенты модели а1 – а3 можно рассматривать как показатели восприимчивости текущего значения популяции к значениям в предыдущие j учетов: 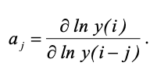 . Эти коэффициенты можно рассматривать как показатели обратной связи в системе, при этом знак коэффициента характеризует тип обратной связи: положительной или отрицательной. Знак коэффициента b при переменной W(i) – суммы температур воздуха в течение трех недель до учета – положительный, то есть чем теплее, тем больше численность коллембол. Таким образом, выполненные расчеты позволяют говорить о достаточной стабильности динамики численности в сообществах коллембол при наличии определенной цикличности плотностей популяций коллембол разных функциональных групп. Изменения в популяциях коллембол можно будет легко оценить по сдвигам абсолютных значений и знаков характеристик ADL-моделей.
. Эти коэффициенты можно рассматривать как показатели обратной связи в системе, при этом знак коэффициента характеризует тип обратной связи: положительной или отрицательной. Знак коэффициента b при переменной W(i) – суммы температур воздуха в течение трех недель до учета – положительный, то есть чем теплее, тем больше численность коллембол. Таким образом, выполненные расчеты позволяют говорить о достаточной стабильности динамики численности в сообществах коллембол при наличии определенной цикличности плотностей популяций коллембол разных функциональных групп. Изменения в популяциях коллембол можно будет легко оценить по сдвигам абсолютных значений и знаков характеристик ADL-моделей.
ЗАКЛЮЧЕНИЕ
Впервые предложена модель динамики сообщества коллембол на основе данных многолетнего мониторинга. Использовано два подхода: 1) применение моделей ADL (autoregression distributed lag) и 2) моделирование сообщества по частям – функциональным группам, связанным с различными приземными ярусами лесного биогеоценоза от почвы до напочвенной растительности. Было выделено три таких группы видов: почвенные, верхнеподстилочные и атмобионтные. Согласно модели, логарифм текущей плотности коллембол в пределах функциональной группы зависит от логарифмов плотности коллембол, оцененных в трех последних выборках и логарифма суммы температур за три последние недели. Для всех групп было показано достоверное соответствие между полевыми данными и ADL-моделью (R2 превышает 0.70). Предложенные модели позволяют анализировать и прогнозировать динамику сообщества коллембол и разрабатывать математические подходы для оценки движущих факторов флуктуации видов и групп видов.
СПИСОК ЛИТЕРАТУРЫ
Базыкин А. Д. Математическая биофизика взаимодействующих популяций. М.: Наука. 1985. 181 с.
Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий. 2003. 368 с.
Вольтерра В. Математическая теория борьбы за существование. М.: Наука. 1976. 288 с.
Гайдук А. Р., Беляев В. Е., Пьявченко Т. А. Теория автоматического управления в примерах и задачах. СПб.: Лань. 2011. 464 с.
Гиляpов М. С. Учет мелких членистоногих (микрофауны) и нематод / В сб. Методы почвенно-зоологических исследований. М.: Наука. 1975. С. 30–43.
Дженкинс Г., Ваттс Д. Спектральный анализ и его приложения. М.: Мир, 1971. Вып. 1. 316 с.; Вып. 2. 287 с.
Дорф Р. К., Бишоп P. X. Современные системы управления. М.: Лаборатория Базовых Знаний, 2004. 832 c.
Исаев А. С., Пальникова Е. Н., Суховольский В. Г., Тарасова О. В. Динамика численности лесных насекомых-филлофагов: модели и прогнозы. М.: Товарищество научных изданий КМК, 2015. 276 с.
Исаев А. С., Хлебопрос Р. Г. Принцип стабильности в динамике численности лесных насекомых // Доклады АН СССР. 1973. Т. 208. Вып. 1. С. 225–228.
Исаев А. С., Хлебопрос Р. Г., Недорезов Л. В., Кондаков Ю. П., Киселев В. В., Суховольский В. Г. Популяционная динамика лесных насекомых. М.: Наука. 2001. 347 с.
Ким Д. П. Теория автоматического управления. М.: Физматлит. 2007. Т. 1. 312 с.
Классификация почв России. М.: Почв. ин-т им. В. В. Докучаева, 1997. 235 с.
Колесов Ю. С. Некоторые задачи математической экологии // Дифференциальные уравнения и их применение. Вильнюс, 1981. № 29. С. 27–35.
Кузнецова Н. А. Коллемболы как модельная группа в биоценологических исследованиях // Чтения памяти академика Меркурия Сергеевича Гилярова. 3-и чтения — 22 декабря 2006 г., Москва. М.: Т-во научных изданий КМК, 2008. С. 11–48.
Левич А. П. Анализ ценозов в экологии сообществ с помощью ранговых распределений // Общая и прикладная ценология. 2007. № 5. С. 14–19.
Марри Дж. Нелинейные дифференциальные уравнения в биологии. Лекции о моделях. М.: Мир, 1983. 397 с.
Мэгарран Э. Экологическое разнообразие и его распределение. М.: Мир. 1992. 181 с.
Потапов М. Б., Кузнецова Н. А. Методы исследования сообществ микроартропод: пособие для студентов и аспирантов. М.: Т-во научных изданий КМК, 2011. 77 c.
Пузаченко Ю. Г. Ранговые распределения в экологии и неэкстенсивная статистическая механика // Сборник трудов ЗИН. 2016. Т. 54. С. 42–71.
Свирежев Ю. М., Логофет Д. О. Устойчивость биологических систем. М.: Наука. 1978. 352 с.
Суховольский В. Г. Экономика живого. Новосибирск: Наука. 2004. 140 c.
Хемминг Р. В. Цифровые фильтры. М.: Недра. 1987. 221 с.
Berryman A. A. On principles, laws and theory in population ecology // Oikos. 2003. Vol. 103. No. 3. P. 695–701.
Berryman A. A. Population systems: a general introduction. New York: Plenum Press, 1981. 222 p.
Bokhorst S., Phoenix G. K., Bjerke J. W., Callaghan T. V., Huyer-Brugman F., Berg M. P. Extreme winter warming events more negatively impact small rather than large soil fauna: shift in community composition explained by traits not taxa // Global Change Biology. 2012. Vol. 18. P. 1152–1162. DOI: 10.1111/j.1365-2486.2011.02565.x.
Britton N. F. Essential mathematical biology. Springer: London, 2003. 335 p.
Bulmer M. G. A statistical analysis of the 10-year cycle in Canada // Journal of Animal Ecology. 1974. No. 43. P. 701–718.
Deng B. An Inverse Problem: Trappers Drove Hares to Eat Lynx // Acta Biotheoretica. 2018. Vol. 66. P. 213–242.
Elton C., Nicholson M. The ten-year cycle in numbers of the lynx in Canada // Journal of Animal Ecology 1942. No. 11. P. 215–244.
Gause G. F. The Struggle for Existence. Baltimore.: Williams and Wilkins, 1934. 163 p.
Gilpin M. E. Do hares eat lynx? // The American Naturalist. 1973. Vol. 107. No. 957. P. 727–730.
Gomatam J. A new model for interacting populations two species systems // Bulletin of Mathematical Biology. 1974. Vol. 36. P. 347–353.
Hassall M., Adl S., Berg M., Griffiths B., Scheu S. Soil fauna–microbe interactions: towards a conceptual framework for research // European Journal of Soil Biology. 2006. Vol. 42. Suppl. 1. P. S54–S60. DOI: 10.1016/j.ejsobi.2006.07.007
Hewitt C. G. The conservation of the wild life of Canada. New York: Charles Scribner′s Sons, 1921. 344 р.
Hopkin S. P. Biology of the springtails: (Insecta: Collembola). Oxford University Press, 1997. 330 p.
Hutchinson G. E. Theory of Competition Between two social species // Ecology. 1947. Vol. 28. P. 319–321.
Isaev A. S, Soukhovolsky V. G., Tarasova O. V., Palnikova E. N., Kovalev A. V. Forest Insect Population Dynamics, Outbreaks and Global Warming Effects. New York: Wiley, 2017. 298 p.
Jucevica E., Melecis V. Global warming affect Collembola community: A long-term study // Pedobiologia. 2006. Vol. 50. No. 2. P. 177–184. DOI: 10.1016/j.pedobi.2005.10.006
Keith L. B. Wildlife’s ten-year cycle. Madison: University of Wisconsin Press. 1963. 221 p.
Kuznetsova N. A. Long-term dynamics of Collembola in two contrast ecosystems // Pedobiologia. 2006. Vol. 50. No. 2. P. 157–164. DOI: 10.1016/j.pedobi.2005.12.004
Kuznetsova N. A. Long-term Dynamics of Collembolan population in Forest and Meadow Ecosystems // Entomological Review. 2007. Vol. 87. No. 1. P. 11–24. DOI: 10.1134/S0013873807010022
Leigh G. The ecological role of Volterra’s equations // Some of Mathematical Problems of Biology. Proceedings of the Symposium of the Mathematical Society. Washington Providence, 1968. P. 1–61.
Levich A. P., Zaburdaeva E. A., Maksimov V. N., Bulgakov N. G., Mamikhin S. V. The Search for Target Values of Quality Indices for Bioindicators of the Ecological State and Environmental Factors: Case Study of Water Bodies of the Don River // Water Resources, 2009. Vol. 36. No. 6. p. 706–717.
Lotka A. J. Elements of Physical Biology. Baltimore.: Williams and Wilkins, 1925. 460 p.
Maaß S., Caruso T., Rillig M. C. Functional role of microarthropods in soil aggregation // Pedobiologia. 2015. Vol. 58. P. 59–63. DOI: 10.1016/j.pedobi.2015.03.001
Matthews T. J, Whittaker R. J. On the species abundance distribution in applied ecology and biodiversity management // Journal of Applied Ecology. 2015. Vol. 52. P. 443–454.
McGill B. J., Etienne R. S., Gray J. S., Alonso D., Anderson M. J., Benecha H. K., White E. P. Species abundance distributions: moving beyond single prediction theories to integration within an ecological framework // Ecology letters. 2007. Vol. 10. No. 10. P. 995–1015.
Odum E. P., Barrett G. W. Fundamentals of ecology. Philadelphia, 1971. 574 p.
Petersen H. Luxton M. A comparative analysis of soil fauna populations and their role in decomposition processes // Oikos. 1982. Vol. 39. P. 288–388. DOI: 10.2307/3544689
Potapov A. M., Guerra C. A., Van den Hoogen J., Babenko A., Bellini B. C., Berg M. P., … & Scheu S. Globally invariant metabolism but density-diversity mismatch in springtails // Nature Communications. 2023. Vol. 14. No. 1. Р. 674. DOI: 10.1038/s41467-023-36216-6
Potapov A., Bellini B. C., Chown S. L., Deharveng L., Janssens F., … & Berg M. P. Towards a global synthesis of Collembola knowledge: challenges and potential solutions // Soil organisms. 2020. Vol. 92. No. 3. Р.161–188. DOI:10.25674/so92iss3pp161
Rohner C. The numerical response of great horned owls to the snowshoe hare cycle: consequences of non-territorial ‘floaters’ on demography // Journal of Animal Ecology. 1996. No. 65. P. 359–370.
Royama T. Analytical population dynamics. L.: Chapman and Hall, 1992. 371 p.
Soukhovolsky V., Kovalev A., Tarasova O., Martemyanov V. Regulatory characteristics of population density dynamics of forest insects and possible reasons for the observed narrow range of such characteristics // Chaos, Solitons and Fractals. 2025. Vol. 191. Article 115949. DOI: 10.1016/j.chaos.2024.115949
Stenseth N. C., Falck W., Bjørnstad O. N., Krebs C. J. Population regulation in snowshoe hare and Canadian lynx: asymmetric food web configurations between hare and lynx // Proceedings of the National Academy of Sciences of the United States of America 1997. No. 94. P. 5147–5152.
Turchin P. Complex Population Dynamics: A Theoretical / Empirical Synthesis. Princeton: Princeton University Press, 2003. 536 p.
Volterra V. Fluctuations in the abundance of a species considered mathematically // Nature. 1926. Vol. 188. P. 558–560.
Whittaker R. H. Dominance and Diversity in Land Plant Communities // Science. 1965. Vol. 147. No. 3655. P. 250–260. DOI: 10.1126/science.147.3655.250
Zhang Z., Tao Y., Li Z. Factors affecting hare–lynx dynamics in the classic time series of the Hudson Bay Company, Canada // Climate Research. 2007. Vol. 34. No. 2. P. 83–89.
Приложение
Таблица. Виды, отнесенные к различным функциональным группам коллембол ельника-кисличника
| A (17 видов) | U (16 видов) |
| Allacma fusca
Anurophorus septentrionalis Caprainea marginata Dicyrtoma fusca Dicyrtomina minuta Entomobrya corticalis Entomobrya marginata Entomobrya nivalis Isotoma viridis Isotomurus sp. Orchesella bifasciata Orchesella flavescens Ptenothrix atra Schoettella ununguiculata Sminthurus viridis Willowsia buski Xenylla sp. |
Ceratophysella denticulata
Desoria hiemalis Deuterosminthurus bicinctus Deuterosminthurus pallipes Entomobryoides myrmecophila Friesea mirabilis Hypogastrura sp. Lepidocyrtus violaceus Pogonognatellus flavescens Proisotoma minuta Pseudachorutes parvulus Sminthurinus aureus Sminthurinus elegans Sminthurinus niger Sphaeridia pumilis Tomocerus vulgaris |
| S (21 вид) | |
| Arrhopalites principalis
Folsomia quadrioculata Folsomides parvulus Isotomiella minor Megalothorax minimus Mesaphorura spp. Micranurida pygmaea Neanura muscorum Neotullbergia crassicuspis Oligaphorura absoloni Oligaphorura serratotuberculata |
Parisotoma notabilis
Proisotoma minima Protaphorura armata Pseudosinella alba Pseudosinella immaculata Stenaphorura quadrispina Willemia anophthalma Willemia denisi Xenylla sp. Xenyllodes armatus |
Рецензенты: к. б. н., ведущий научный сотрудник Шанин В. Н.,
к. б. н., старший научный сотрудник Куприн А. В.
[1] Прим. редакции: в лесной экологии под термином «окно» (gap) обычно понимают большой прорыв в пологе леса, образовавшийся в результате вывала/слома одного или нескольких нескольких деревьев





