MATHEMATICAL MODELING OF THE FOREST FIRE IMPACT ON THE BRANCH OF A CONIFEROUS TREE
С текстом оригинальной статьи Вы можете ознакомиться по ссылке
Original Russian Text © 2021 N. V. Baranovskiy, D. S. Menshikov published in Forest Science Issues Vol. 4, No. 2, Article 85
N.V. Baranovskiy1, D. S. Menshikov2
1Tomsk Polytechnic University,
Lenin Ave. 30, Tomsk 634050, Russian Federation
2State Specialized Design Institute
Bohdan Khmelnitsky st. 2, Novosibirsk 630075, Russian Federation
E-mail: firedanger@yandex.ru
Received 17 February 2021
Revised 14 June 2021
Accepted 29 June 2021
It is necessary to develop quantitative methods to assess the formation of thermal burns in the morphological parts of coniferous trees. The purpose of the study is mathematical modeling of heat transfer in the layered structure of a coniferous tree branch under the influence of a forest fire front. The heat propagation in the «branch — needles — flame zone» system is described by a system of non-stationary differential equations of heat conduction with the corresponding initial and boundary conditions. As an object of research, a digital model of a branch of a coniferous tree for various species, namely, pine, larch and fir, was used. Temperature distributions are obtained for different variants of the branch structure and conditions of the impact of the forest fire front. Conclusions are made about the need for further modernization of the mathematical model. The developed model is the basis for creating software tools for specialized geographic information systems.
Keywords: forest fire, branch, heat transfer, impact, thermal injure
Forest fires are currently a real disaster for a number of countries in the world community, as forest fires have turned from a natural regulating factor into a catastrophic phenomenon. As a result of forest fires, the atmosphere is polluted, forest stands die, industrial timber stocks are destroyed, chronic diseases are exacerbated, and rural settlements are destroyed. One of the important problems is the death of individual trees or entire forest stands as a result of forest fires (Baranovskiy, Kuznetsov, 2017; Baranovskiy, 2020). Currently, research is being widely conducted within the framework of quantitative ecology, which studies the dynamics of individual ecological systems and includes mathematical models of individual ecological processes (Shilov, 2003). Existing methods for assessing the environmental consequences of forest fires are based mainly on the assessment of statistical and factual material (Michaletz, Johnson, 2007; Yakimov, Ponomarev, 2020).
Thermal injury resulting from a forest fire can trigger a whole set of complex mechanisms for changing the physiology of trees in the post-fire period (Bar et al., 2019). The effects of wildfire impact on trees can manifest themselves in different ways depending on the characteristics of a particular wildfire (Michaletz, Johnson, 2007; O’Brien et al., 2018). High-intensity crown forest fires burn living and dead biomass in the tree crown. Burning of all foliage or needles and meristems can cause immediate tree death if the tree is not able to sprout from heat-resistant organs (Clarke et al., 2013; Pausas, Keeley, 2017). The consequences of forest fires for two types of trees differ: primary and secondary (Michaletz, Johnson, 2007). Primary effects are a direct consequence of heat transfer from the combustion zone of forest fuels to the root system, trunk and crown of a tree (Michaletz, Johnson, 2007; Bergman, Incropera, 2011). Tree tissue death caused by protein denaturation generally occurs at 60 °C (Rosenberg et al., 1971). However, the rate of cell death increases exponentially with temperature. That is, lower temperatures can also lead to cell death in the case of prolonged exposure to elevated temperatures (Hare, 1961; Dickinson, Johnson, 2004). Heat transfer from the burning zone to the crown of a tree can cause immediate necrosis of buds or foliage, as well as damage to the cambium and phloem of branches. The degree of damage to crown components depends on their thermophysical properties and the characteristics of the forest fire, as well as the height of the lower boundary of the tree crown (van Wagner, 1973; Michaletz, Johnson, 2006, 2007). In large canopy components, such as branches, there is an internal temperature gradient and the process of heat conduction within this component becomes important. It is important to understand that the conduction velocity decreases with the radial coordinate and therefore the thickness and properties of the cortical layer are important (Michaletz et al., 2013; Pounden et al., 2014). The secondary effects of forest fires are more complex and their mechanisms are not yet fully understood. The response of vegetation functions to thermal damage can vary widely (Bar et al., 2019). On the one hand, trees after a forest fire can demonstrate a violation of physiological activity, reduced growth, and delayed death (Lambert, Stohlgren, 1988; van Mantgem, Schwartz, 2003; van Mantgem et al., 2011; Thompson et al., 2017). On the other hand, it is known that injured trees can be superior in the short to medium term (Pearson et al., 1972; Battipaglia et al., 2014; Valor et al., 2018).
However, it is necessary to develop mathematical methods for assessing the consequences of the impact of forest fire damaging factors on trees and their individual parts. In particular, it is important to understand the processes of formation of thermal damage to the branch of a coniferous tree. In this regard, the following goal of the study is formulated.
Purpose of the work is to mathematically model heat transfer in the branches of a coniferous tree under the influence of elevated temperature from the front of a forest fire.
MATERIALS AND METHODS
Object of study: coniferous trees, namely, pine, larch, fir (Lesoteka, 2020). The subject of research is the mathematical modeling of the heat transfer process in the branches of a coniferous tree.
The method of finite differences is used to solve a differential equation in partial derivatives (Samarsky, Vabishchevich, 2003). The coniferous branch represents a cylindrical system. The flame front of a forest fire acts on the branch. The boundary condition of the first kind at the boundary of the branch sets the temperature value for each moment of time. For a cylindrical system, the heat conduction equation will have the form:
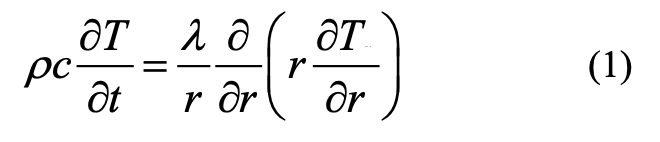 .
.
In its final form, equation (1) after approximation of partial derivatives is presented in the following form:
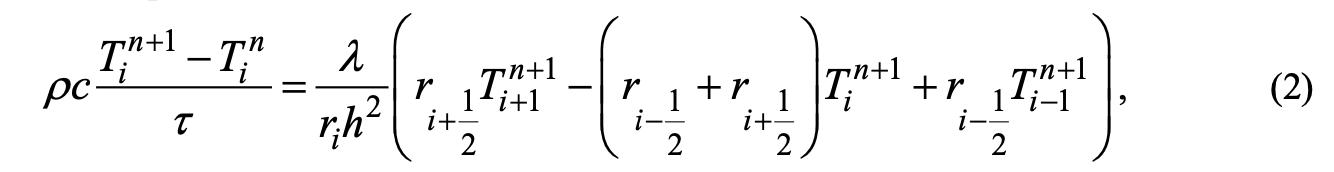
where ρ, c, λ, T – density, heat capacity, thermal conductivity and temperature of the material; r is the spatial coordinate; t is time; n is the layer number in time; i is the number of the node in the spatial coordinate; τ and h are steps in time and space.
Computational experiments were carried out taking into account the initial data presented in tables 1–4.
Table 1. Thermophysical properties of the environment (Grishin, 1997)
| Part
(Fig.1) |
Title | Characteristics | ||
| ρ, kg/m3 | с, J/kg K | λ, W/m K | ||
| 4 | Flame zone | 0.656 | 2483 | 0.1836 |
Table 2. Thermophysical properties of branches (Grishin, 1997)
| Pine | ||||||||
| ρ, kg/m3 | с, J/kg K | λ, W/m K | ||||||
| Core | Bark | Needles | Core | Bark | Needles | Core | Bark | Needles |
| 500 | 500 | 500 | 1800 | 1670 | 1400 | 0.12 | 0.12 | 0.102 |
| Larch | ||||||||
| 660 | 660 | 500 | 2170 | 2170 | 1400 | 0.13 | 0.13 | 0.102 |
| Fir | ||||||||
| 450 | 450 | 500 | 2700 | 2700 | 1400 | 0.15 | 0.15 | 0.102 |
Table 3. Geometric dimensions of the branch
| № | Parameter | Core | Bark | Needles |
| 1 | Width (r, м) | 0.008 | 0.011 | 0.041 |
| 2 | Width (r, м) | 0.008 | 0.012 | 0.045 |
| 3 | Distance (r, м) | 0.008 | 0.013 | 0.049 |
Table 4. Temperature range in the flame zone
| Branch | Pine | Larch | Fir |
| Tf , °C | 800, 900, 1000 | 800, 900, 1000 | 800, 900, 1000 |
RESULTS AND DISCUSSION
The physical model of the forest fire impact on the branch of a coniferous tree is formulated taking into account the following assumptions:
- A one-dimensional setting is considered.
- The multilayer structure of the branch is considered.
- The monolithic structure of the branch is considered.
- Heat transfer in the «branch-needles-flame zone» system due to conduction.
- Thermophysical parameters do not depend on temperature.
- The evaporation of moisture is neglected.
- Pyrolysis of dry organic matter is neglected.
- The source of the temperature rise is modeled by specifying an area of elevated temperature near the branch.
- The situation when the source is stationary is considered.
The branch is a cylindrical system, which includes the core of the branch, the bark layer and the layer of needles. The branch interacts with the flame zone. The graphic image is shown in Figure 1. The impact of a forest fire is described by the boundary conditions of the first kind.
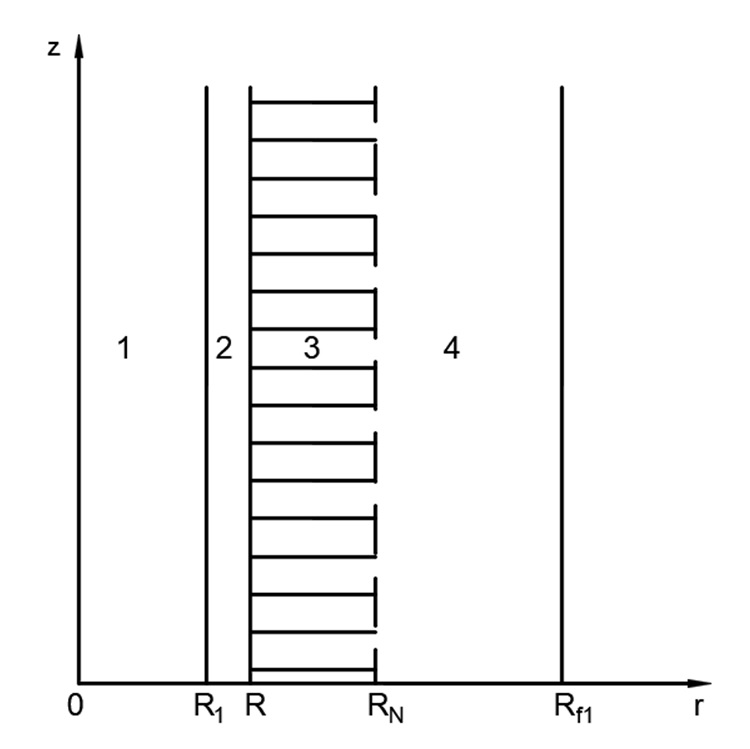
Figure 1. Geometry of the solution area: 1 — core, 2 — bark, 3 — needles,
4 — flame zone
Mathematically, the process of forest fire impact is described by a system of heat conduction equations:
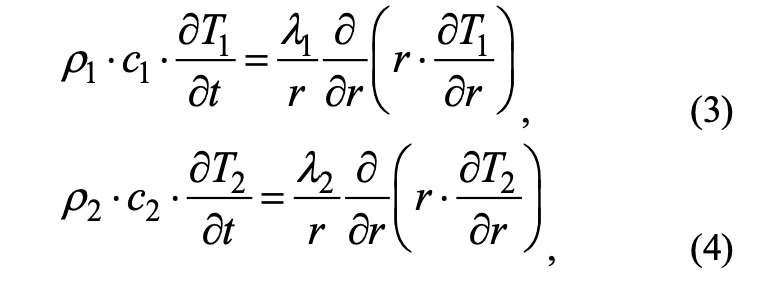
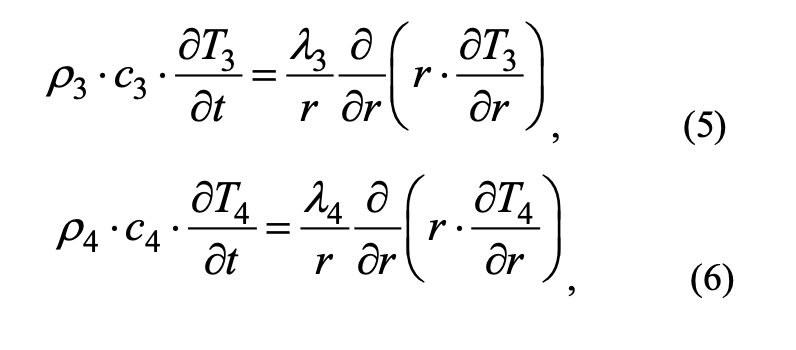
Boundary conditions:
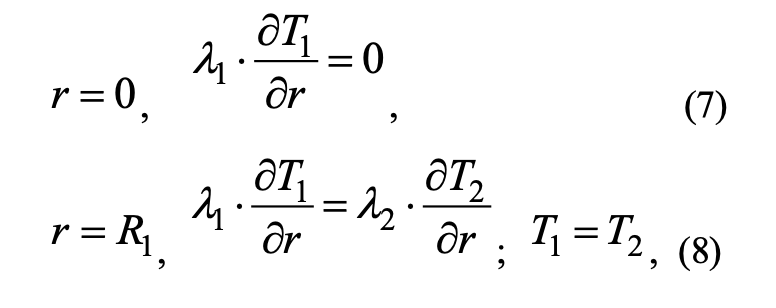
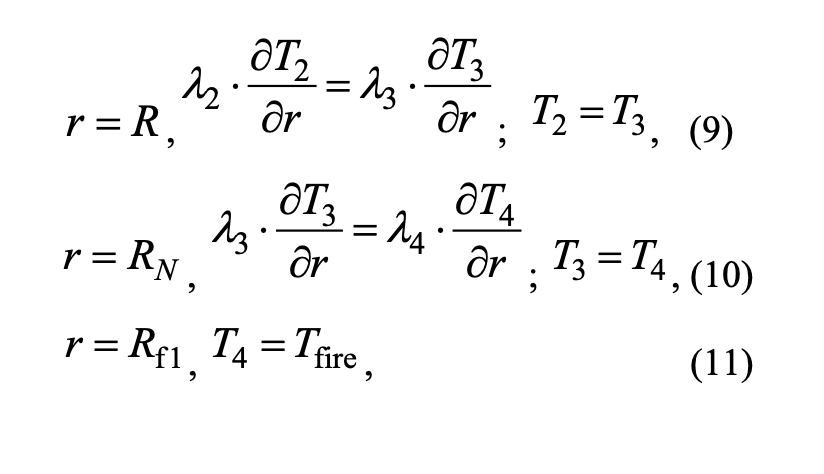
Initial conditions:
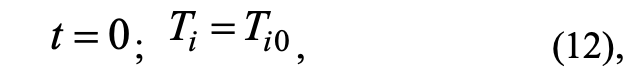
where ρi, сi, Ti, λi — density, heat capacity, temperature, thermal conductivity (i = 1 — the core of the branch, i = 2 — the bark, i = 3 — needles, i = 4 — flame zones); Tfire — temperature in the fire front; t is time; r is the spatial coordinate; R1 — border of the core and bark; R is the boundary of the bark and the layer of needles; RN is the boundary of the outer layer of needles; Rf1 is the boundary of the solution area. Index «0» is responsible for the parameter at the initial time.
The presented system of equations with the corresponding initial and boundary conditions is solved using the finite difference method. Finite-difference analogues of differential equations are solved by the marching method (Samarsky, Vabishchevich, 2003).
The process of thermal impact of a forest fire front on a branch of a coniferous tree is due to heat transfer due to conduction in the layered structure of the branch. Heating is carried out at the outer boundary of the branch and is mathematically described by the boundary conditions of the first kind, which simulate the effect of the flame zone. Further, heat is transferred from a more heated area to a less heated area.
Based on the results of computational experiments, graphical dependencies were constructed demonstrating the temperature distribution in the «branch — needle — flame zone» system.
Figures 2–4 show the temperature distributions in the «branch — needles — flame zone» system for various scenarios of the impact of a forest fire on a pine branch.
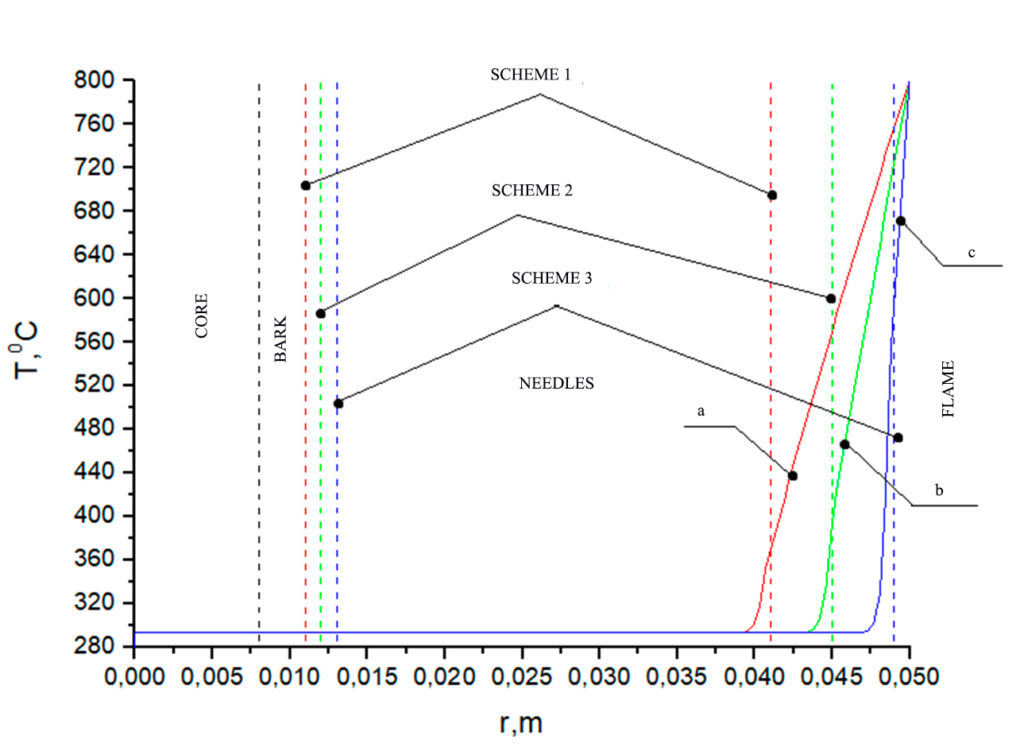
Figure 2. Temperature distribution at Tfire = 800 °C on a pine branch according to the relevant schemes (table 3): a) with a bark thickness of 0.011 m and a needle length of 0.041 m, b) with a bark thickness of 0.012 m and a needle length of 0.045 m, c) with a bark thickness of 0.013 m and a needle length of 0.049 m. Heating time 1 s
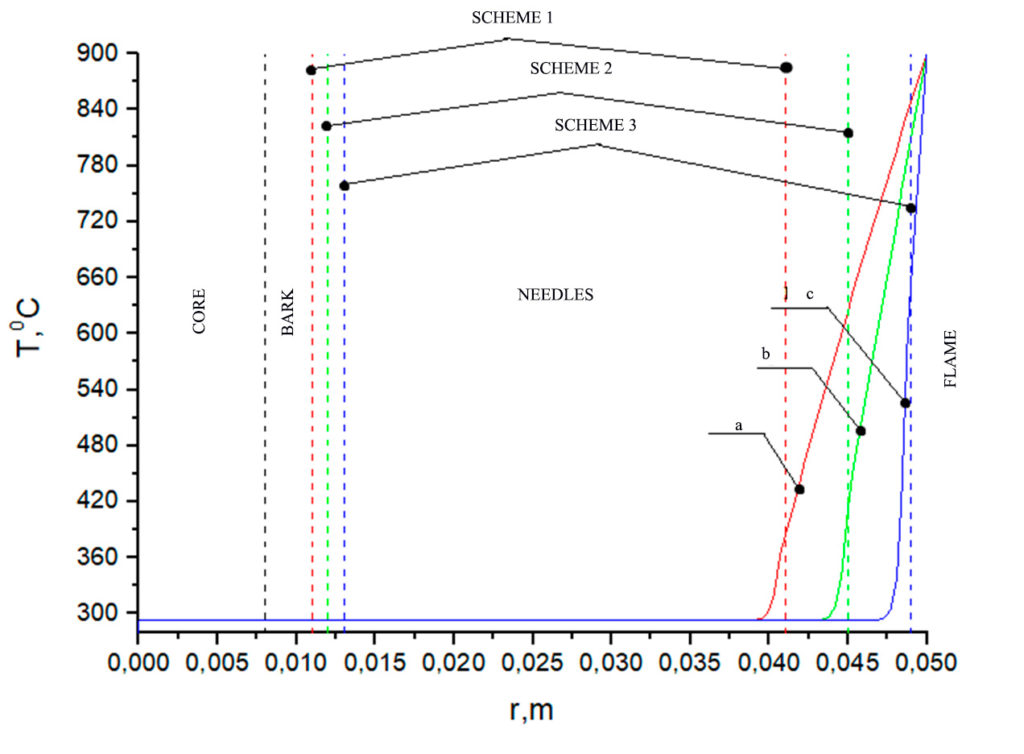
Figure 3. Temperature distribution at Tfire = 900 °C on a pine branch according to the relevant schemes (table 3): a) with a bark thickness of 0.011 m and a needle length of 0.041 m, b) with a bark thickness of 0.012 m and a needle length of 0.045 m, c) with a bark thickness of 0.013 m and a needle length of 0.049 m. Heating time 1 s
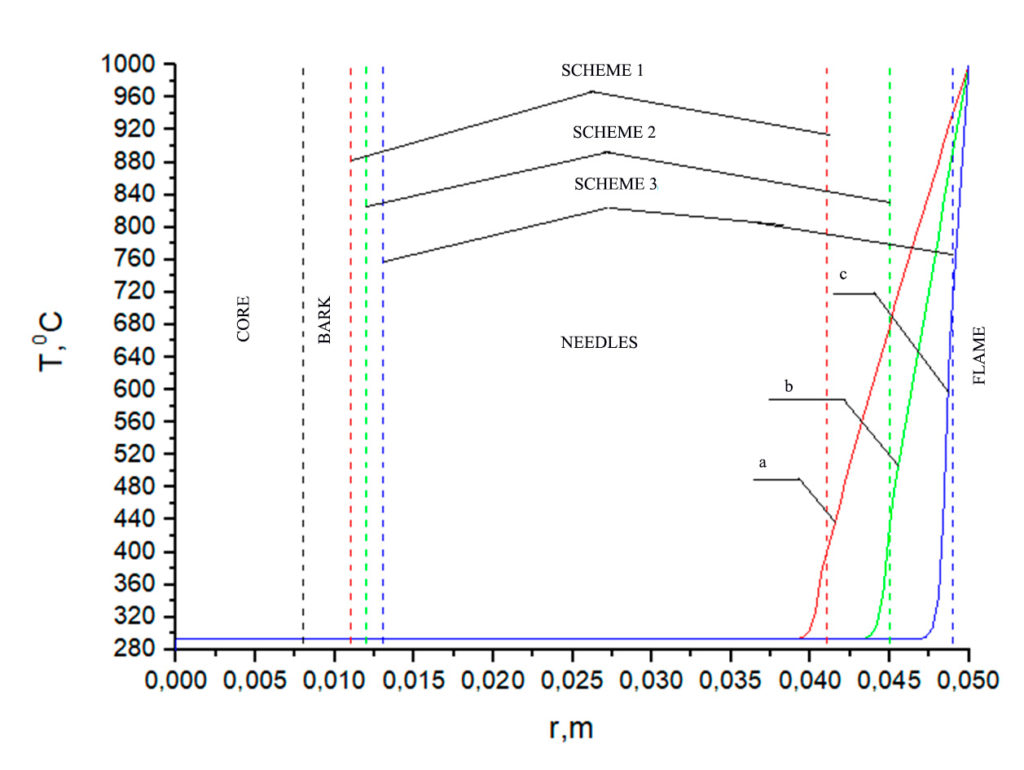
Figure 4. Temperature distribution at Tfire=1000 °C on a pine branch according to the relevant schemes (table 3): a) with a bark thickness of 0.011 m and a needle length of 0.041 m, b) with a bark thickness of 0.012 m and a needle length of 0.045 m, c) with a bark thickness of 0.013 m and a needle length of 0.049 m. Heating time 1 s
Figures 5–7 show the temperature distributions in the «branch — needles — flame zone» system for various scenarios of the impact of a forest fire on a larch branch.
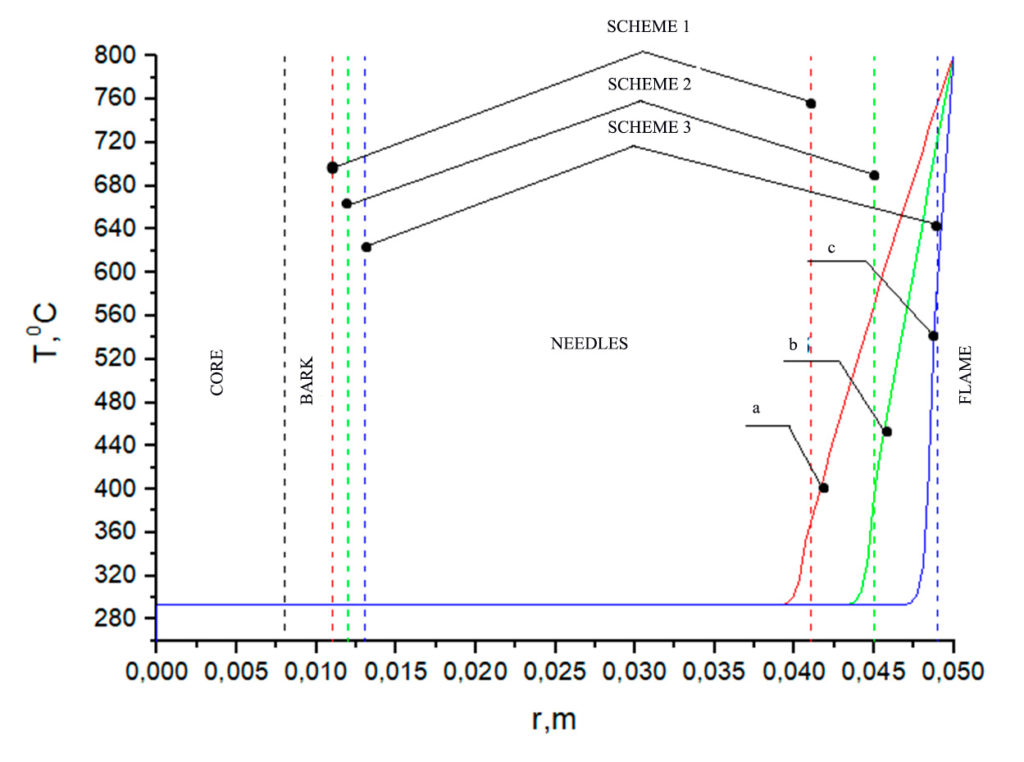
Figure 5. Temperature distribution at Tfire = 800 °C on a larch branch according to the relevant schemes (table 3): a) with a bark thickness of 0.011 m and a needle length of 0.041 m, b) with a bark thickness of 0.012 m and a needle length of 0.045 m, c) with a bark thickness of 0.013 m and a needle length of 0.049 m. Heating time 1 s
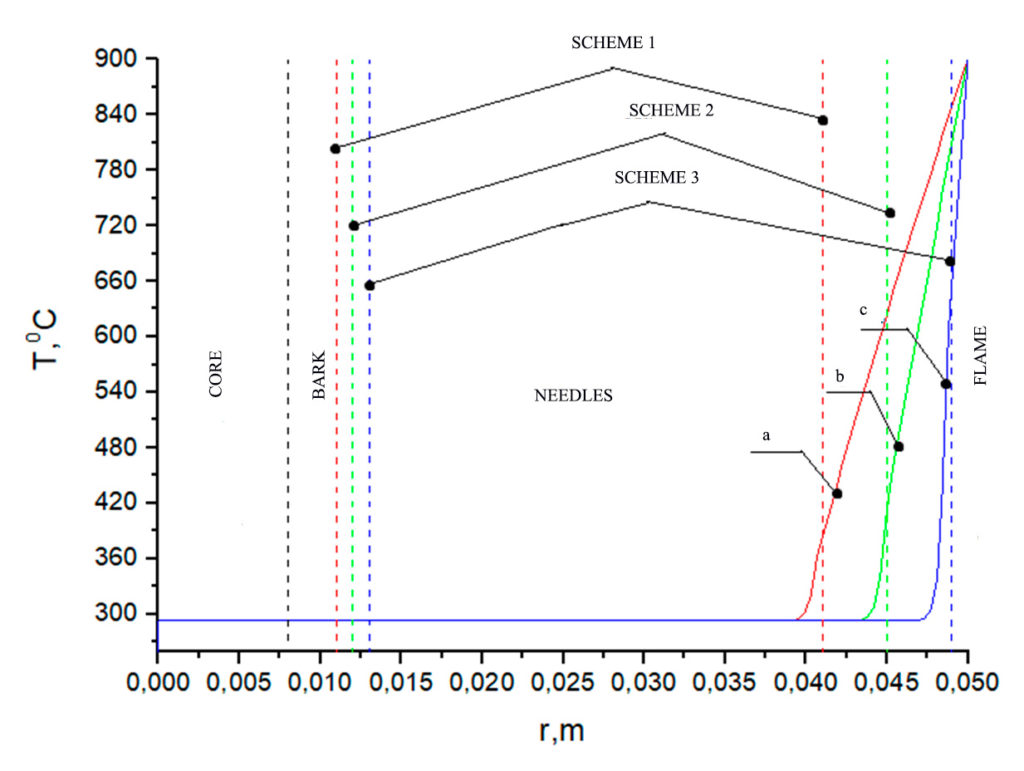
Figure 6. Temperature distribution at Tfire = 900 °C on a larch branch according to the relevant schemes (table 3): a) with a bark thickness of 0.011 m and a needle length of 0.041 m, b) with a bark thickness of 0.012 m and a needle length of 0.045 m, c) with a bark thickness of 0.013 m and a needle length of 0.049 m. Heating time 1 s
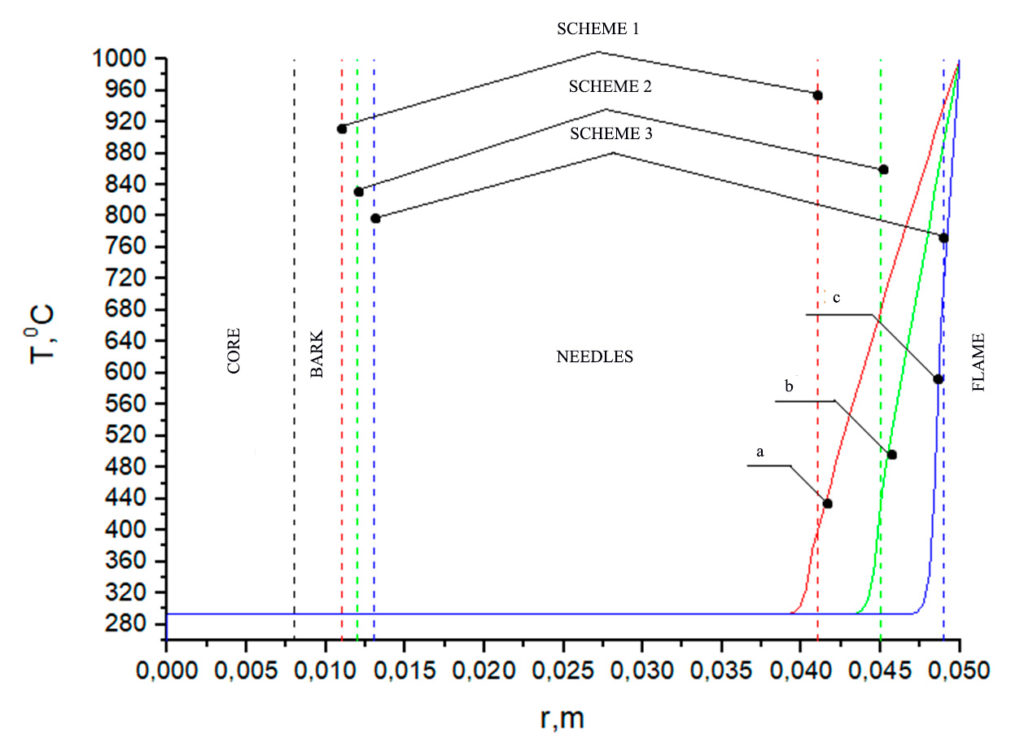
Figure 7. Temperature distribution at Tfire = 1000 °C on a larch branch according to the corresponding schemes (table 3): a) with a bark thickness of 0.011 m and a needle length of 0.041 m, b) with a bark thickness of 0.012 m and a needle length of 0.045 m, c) with a bark thickness of 0.013 m and a needle length of 0.049 m. Heating time 1 s
Figures 8–10 show the temperature distributions in the «branch — needles — flame zone» system for various scenarios of the impact of a forest fire on a fir branch.
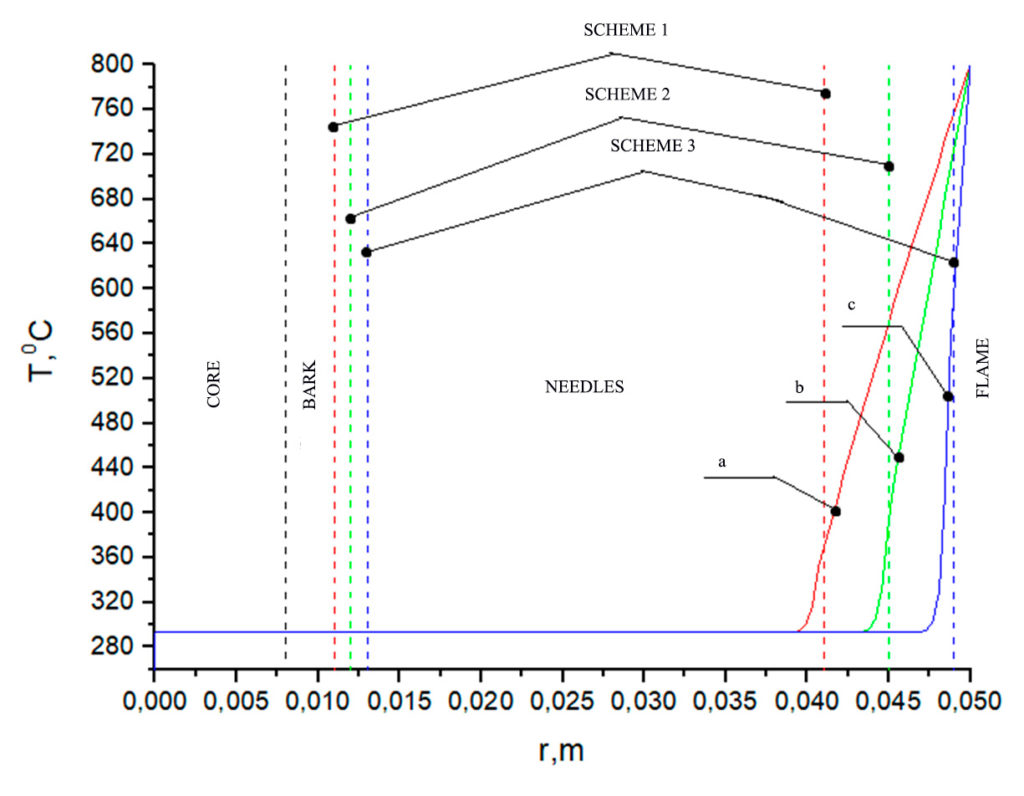
Figure 8. Temperature distribution at Tfire = 800 °C on a fir branch according to the relevant schemes (table 3): a) with a bark thickness of 0.011 m and a needle length of 0.041 m, b) with a bark thickness of 0.012 m and a needle length of 0.045 m, c) with a bark thickness of 0.013 m and a needle length of 0.049 m. Heating time 1 s
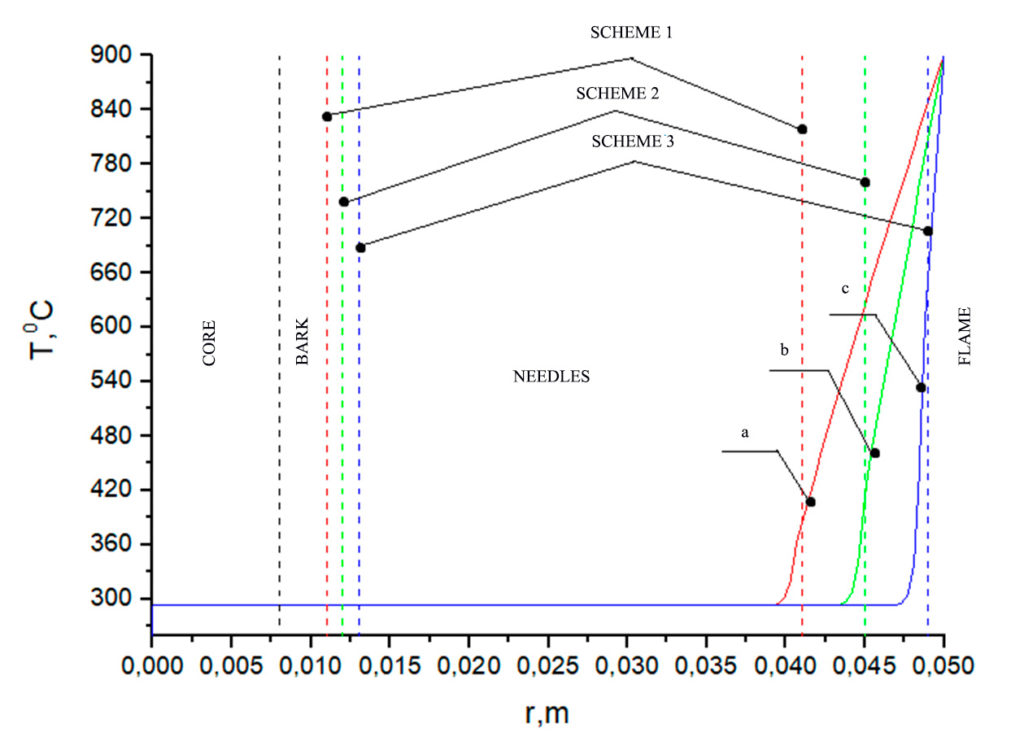
Figure 9. Temperature distribution at Tfire = 900 °C on a fir branch according to the relevant schemes (table 3): a) with a bark thickness of 0.011 m and a needle length of 0.041 m, b) with a bark thickness of 0.012 m and a needle length of 0.045 m, c) with a bark thickness of 0.013 m and a needle length of 0.049 m. Heating time 1 s
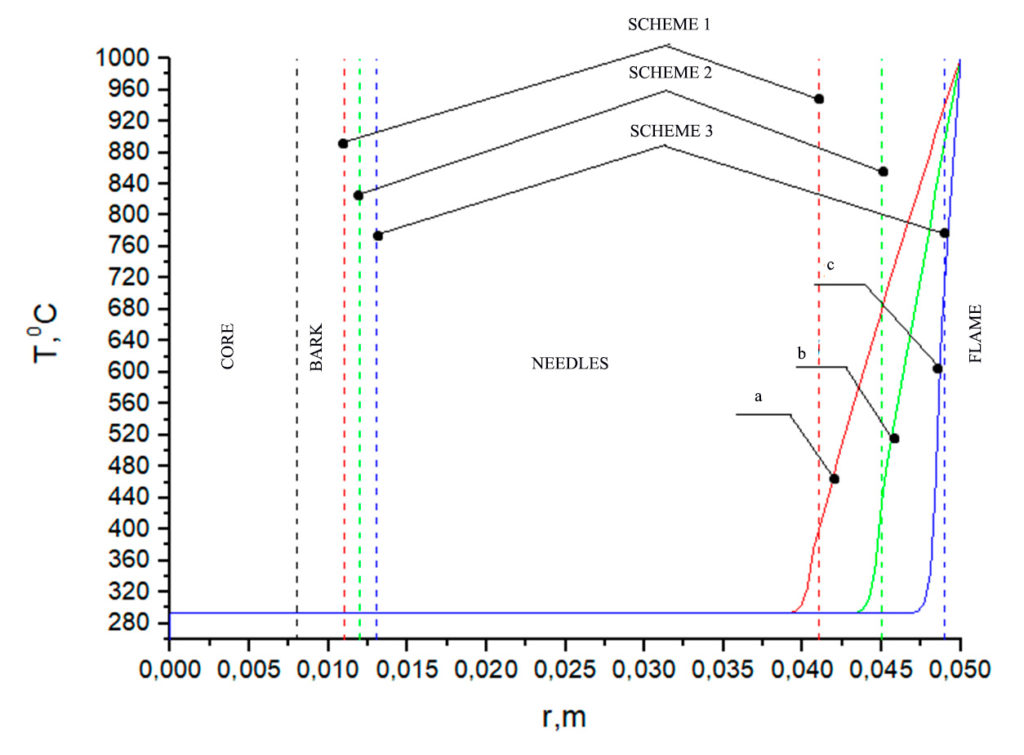
Figure 10. Temperature distribution at Tfire=1000 °C on a fir branch according to the relevant schemes (table 3): a) with a bark thickness of 0.011 m and a needle length of 0.041 m, b) with a bark thickness of 0.012 m and a needle length of 0.045 m, c) with a bark thickness of 0.013 m and a needle length of 0.049 m. Heating time 1 s
An analysis of the temperature dependences in Figures 2–4 shows that for all geometry schemes of the solution area, an increased temperature is observed in the upper part of the needles during the specified time interval of exposure to the forest fire flame. The closer the needle is to the flame front, the higher the temperature at its end. When exposed to a low-intensity surface fire at the end of a pine needle, temperatures of the order of 360 °C are observed for scheme a and 400 °C, 600 °C for schemes b and c, while during a high-intensity surface fire, these temperatures are respectively 390 °C, 460 °C, 660 °C. The crown forest fire leads to heating of the needles to temperatures of the order of 400 °C, 480 °C, 720 °C. The analysis of temperature dependences in Figures 5–7 (larch) and Figures 8–10 (fir) demonstrates similar temperatures at the end of the needles for all types of forest fires considered. At temperatures up to 400 °C, intensive thermal decomposition of the dry organic material of the needles occurs. At a higher temperature, ignition of the needles can already be observed, which can lead to irreversible consequences for a separately considered coniferous tree.
It should be noted that the burning of all needles and meristem can cause immediate death of the tree if the tree is not able to sprout from heat-resistant organs (Clarke et al., 2013; Pausas, Keeley, 2017).
Thus, mathematical modeling of the thermal impact from the flame of a forest fire on a branch of a coniferous tree was carried out. Three impact scenarios by forest fire type are considered: low intensity surface fire (800 °C), high intensity surface fire (900 °C) and crown forest fire (1000 °C). Three different schemes were also explored, describing the various geometric structures of a branch of a coniferous tree. It is clear that these are approximate data and in a real situation the geometry of a branch can differ significantly from the type of tree, the growing season and age of the tree, as well as its physiological state. Using only a thermophysical model to study heat transfer in a coniferous tree branch showed that the temperature distributions for different species are quite similar. This means that further modernization of this mathematical model is necessary. Thus, it is necessary to take into account the evaporation of moisture and the thermal decomposition of dry organic matter. In addition, subsequent studies should take into account data on the physiological activity of various species and experimental data on the death of tree tissues at various temperatures. That is, it is necessary to supplement the developed mathematical model with criteria for damage to branch tissues depending on the temperature in the forest fire front and the duration of exposure. Another way to improve the mathematical model can be to take into account convective and radiant heat transfer at the outer boundary of the branch directly exposed to the damaging factors of a forest fire. In the future, such a mathematical model can be used as a basis for creating software tools in specialized geoinformation systems for monitoring the state of forest stands and predicting their functioning in the post-fire period.
CONCLUSION
Thus, as a result of the study, a basic mathematical model of heat transfer in the layered structure of a coniferous tree branch was developed based on non-stationary differential equations of heat conduction with appropriate initial and boundary conditions. A preliminary analysis of the results obtained shows that the use of only developments in the field of heat transfer does not give a clear answer to questions regarding the formation of thermal lesions in the branches of various coniferous species. It is necessary to integrate into the mathematical model quantitative and qualitative criteria for the formation of thermal lesions, developed on the basis of an analysis of physiological processes and experiments on the effect of elevated temperature on wood tissues.
ACKNOWLEDGEMENTS
This work was financially supported by the Russian Foundation for Basic Researches. Scientific project Nо 17-29-05093.
REFERENCES
Bar A., Michaletz S. T., Mayr S., Fire effects on tree physiology, New Phytologist, 2019, Vol. 223, pp. 1728–1741.
Baranovskiy N. V., Kuznetsov G. V., Forest fire occurrences and ecological impact prediction: monograph. Novosibirsk: Publishing House of the Siberian Branch of the Russian Academy of Science, 2017, 259 p.
Baranovskiy N. V., Predicting, Monitoring, and Assessing Forest Fire Dangers and Risks. IGI Global, 2020, 477 p.
Battipaglia G., Strumia S., Esposito A., Giuditta E., Sirignano C., Altieri S., Rutigliano F. A., The effects of prescribed burning on Pinus halepensis Mill. as revealed by dendrochronological and isotopic analysis, Forest Ecology and Management, 2014, Vol. 334, pp. 201–208.
Bergman T. L., Incropera F. P., Fundamentals of heat and mass transfer, Hoboken, NJ, USA: John Wiley & Sons, 2011, 1048 p.
Clarke P. J., Lawes M. J., Midgley J. J., Lamont B. B., Ojeda F., Burrows G. E., Enright N. J., Knox K. J. E., Resprouting as a key functional trait: How buds, protection and resources drive persistence after fire, New Phytologist, 2013, Vol. 197, pp. 19–35.
Dickinson M. B., Johnson E. A., Temperature-dependent rate models of vascular cambium cell mortality, Canadian Journal of Forest Research, 2004, Vol. 559, pp. 546–559.
Grishin A. M., Mathematical modeling of forest fire and new methods of fighting them. Russia. Tomsk: Publishing House of the Tomsk State University, 1997, 390 р.
Hare R. C., Heat effects on living plants. Occasional Paper 183. New Orleans, LA, USA: USDA Forest Service, Southern Forest Experiment Station, 1961, 34 p.
Lambert B. S., Stohlgren T. J., Giant sequoia mortality in burned and unburned stands, Journal of Forestry, 1988, Vol. 86, pp. 44–46.
Lesoteka, 2020, https://lesoteka.com/ (2021, 17 February)
Michaletz S. T., Johnson E. A., A heat transfer model of crown scorch in forest fires, Canadian Journal of Forest Research, 2006, Vol. 36, pp. 2839–2851.
Michaletz S. T., Johnson E. A., How Forest fires kill trees: a review of the fundamental biophysical processes, Scandinavian Journal of Forest Research, 2007, Vol. 22, pp. 500–515.
Michaletz S. T., Johnson E. A., Mell W. E., Greene D. F., Timing of fire relative to seed development may enable non-serotinous species to recolonize from the aerial seed banks of fire-killed trees, Biogeosciences, 2013, Vol. 10, pp. 5061–5078.
O’Brien J. J., Hiers J. K., Varner J. M., Hoffman C. M., Dickinson M. B., Michaletz S. T., Loudermilk E. L., Butler B. W., Advances in mechanistic approaches to quantifying biophysical fire effects, Current Forestry Reports, 2018, Vol. 4, pp. 161–177.
Pausas J. G., Keeley J. E., Epicormic resprouting in fire-prone ecosystems, Trends in Plant Science, 2017, Vol. 22, pp. 1008–1015.
Pearson H. A., Davis J. R., Schubert G. H., Effects of wildfire on timber and forage production in Arizona, Journal of Range Management, 1972, Vol. 25, pp. 250–253.
Pounden E., Greene D. F., Michaletz S. T., Non-serotinous woody plants behave as aerial seed bank species when a late-summer wildfire coincides with a mast year, Ecology and Evolution, 2014, Vol. 4, pp. 3830–3840.
Rosenberg B., Kemeny G., Switzer R. C., Hamilton T. C., Quantitative evidence for protein denaturation as the cause of thermal death, Nature, 1971, Vol. 232, pp. 471–473.
Samarskiy A. A., Vabishchevich P. N., Vychislitelnaya teploperedacha (Computational heat transfer). Moscow: Editorial URSS, 2003, 784 p.
Shilov I. A., Ecologia (Ecology), Moscow: High School, 2003, 512 p.
Thompson M. T. C., Koyama A., Kavanagh K. L., Wildfire effects on physiological properties in conifers of central Idaho forests, USA, Trees, 2017, Vol. 31, pp. 545–555.
Valor T., Casals P., Altieri S., Gonzalez-Olabarria J. R., Pique M., Battipaglia G., Disentangling the effects of crown scorch and competition release on the physiological and growth response of Pinus halepensis Mill. Using δ13C and δ18O isotopes, Forest Ecology and Management, 2018, Vol. 424, pp. 276–287.
van Mantgem P., Schwartz M., Bark heat resistance of small trees in Californian mixed conifer forests: testing some model assumptions, Forest Ecology and Management, 2003, Vol. 178, pp. 341–352.
van Mantgem P., Stephenson N. L., Knapp E., Battles J., Keeley J. E., Long-term effects of prescribed fire on mixed conifer structure in the Sierra Nevada, California, Forest Ecology and Management, 2011, Vol. 261, pp. 989–994.
van Wagner C. E., Height of crown scorch in forest fires, Canadian Journal of Forest Research, 1973, Vol. 3, pp. 373–378.
Yakimov N., Ponomarev E., Dynamics of post-fire effects in larch forests of Central Siberia based on Satellite data, E3S Web of Conference, 2020, Vol. 149, Article Nо 03008.
Reviewer: Candidate of Technical Sciences P. N. Goman





