- DOI 10.31509/2658-607x-202252-112
- УДК 574.474
Моделирование динамики лесных экосистем с учётом их структурной неоднородности на разных функциональных и пространственных уровнях
© 2022 г. В. Н. Шанин1, 2, П. В. Фролов1, И. В. Припутина1, О. Г. Чертов3, С. С. Быховец1, Е. В. Зубкова1, А. М. Портнов1, Г. Г. Фролова1, М. Н. Стаменов1, П. Я. Грабарник1
1Институт физико-химических и биологических проблем почвоведения РАН — обособленное подразделение Федерального исследовательского центра «Пущинский научный центр биологических исследований Российской академии наук»
Россия, 142290, Московская обл., г. Пущино, ул. Институтская, д. 2, корп. 2.
2Центр по проблемам экологии и продуктивности лесов РАН
Россия, 117997, г. Москва, ул. Профсоюзная, 84/32, стр. 14
3Бингенский политехнический университет
Федеративная Республика Германия, 55411, Бинген, ул. Берлин, 109
E-mail: shaninvn@gmail.com
Поступила в редакцию: 08.09.2022
После рецензирования: 15.10.2022
Принята к печати: 28.10.2022
Во многих задачах современной лесной экологии требуется анализ сопряжённой динамики процессов, происходящих на разных пространственно-временных масштабах функционирования растительных сообществ и почв в их взаимодействии под влиянием всех эдафических и антропогенных факторов. Эффективным инструментом подобного анализа являются математические модели. Цель данной работы — представить реализацию новой системы моделей, позволяющей воспроизводить в имитационных экспериментах пространственную структуру лесных фитоценозов, формируемую древесным и травяно-кустарничковым ярусами, и связанные с этим неоднородность почвенных условий и разнообразие экологических ниш на разных иерархических уровнях. Для определения необходимого уровня детализации пространственной неоднородности лесных биогеоценозов, связанной с процессами их разномасштабного функционирования, проведены экспериментальные исследования на постоянных пробных площадях в Приокско-Террасном государственном природном биосферном заповеднике и в государственном природном заповеднике «Калужские засеки». Пространственная структура сообществ и неоднородность экологических условий в них изучались с использованием традиционных почвенно-геоботанических и современных инструментальных методов. Полученные данные использованы для обоснования алгоритмов и параметризации разных блоков новой системы моделей. Программная реализация пространственно-детализированной процессной системы моделей показала её способность воспроизводить динамику лесных экосистем с учётом видовой и пространственной структуры разных ярусов растительности и связанной с этим мозаичности почвенных условий. За счёт реализованного в данной системе моделей широкого спектра взаимосвязанных экосистемных характеристик появилась возможность выполнять имитационные оценки продуктивности, биогенного круговорота C и N и динамики лесных экосистем с учётом характерной для них разномасштабной пространственной структуры. Это позволяет улучшить понимание экосистемных процессов и их вклад в поддержание устойчивого функционирования лесов, что может быть использовано для прогнозных оценок эффективности лесопользования и в других лесоводственных и экологических задачах.
Ключевые слова: имитационные модели, пространственная структура, продуктивность древостоев, травяно-кустарничковый ярус, лесные почвы, элементы питания, круговорот углерода
ВВЕДЕНИЕ
Сохранение биоразнообразия и биосферных функций лесного покрова Земли невозможно без выявления механизмов устойчивого поддержания структуры и функционирования лесных экосистем, которые, в случае старовозрастных лесов, характеризуются многовидовым и, как правило, многоярусным и разновозрастным составом, а также высокой пространственной неоднородностью почвенного покрова, и в которых обеспечивается необходимая смена поколений, в том числе определяющая сукцессионную динамику экосистем.
Неотъемлемой характеристикой всех наземных экосистем является их пространственная структура (Восточноевропейские леса …, 2004; Карпачевский, 1981). Она проявляется, например, в горизонтальном и вертикальном расположении растений в биогеоценозе и вертикальной структуре полога. Также пространственная структура определяет многие процессы в почве. Интерес к анализу пространственной структуры сообществ и её изменений обусловлен предположением, что данный анализ может помочь в изучении экологических процессов, происходящих в сообществе. Общепринято, что пространственная структура сообществ является показателем разнообразия местообитаний и полноты использования растениями ресурсов среды. Именно от взаимного пространственного расположения отдельных особей во многом зависят такие важные биологические процессы в растительных сообществах, как успешное возобновление видов и конкуренция за ресурсы (Колобов и др., 2015; Kolobov, Frisman, 2018). Столь же актуальны вопросы, связанные с анализом механизмов формирования обратных связей между функционированием биоты и средой её обитания (в частности, почвенным покровом), которые проявляются на разных иерархических уровнях и с разными характерными временами. Совместное действие различных экологических процессов может быть разнонаправленным (уменьшающим результирующий эффект) или со-направленным (ускоряющим время и/или усиливающим интенсивность его проявления), и, кроме того, может иметь специфические особенности на разных пространственных масштабах. Тем не менее, часто удаётся показать, что наблюдаемая сложность процессов может являться результатом композиции простых взаимодействий между особями, в первую очередь определяемых пространственной структурой, которая, в свою очередь, формируется под действием данных процессов.
Проблема совместного анализа структуры и масштаба является одной из важнейших проблем экологии, объединяющей биологию популяций и науку об условиях окружающей среды (эдафологию) и связывающей фундаментальную и прикладную экологию (Levin, 1992). В большом числе актуальных задач, таких как прогноз экологических последствий глобального изменения климата, сохранение биоразнообразия и устойчивости экосистем, требуется изучение явлений, происходящих в самых разных масштабах пространства, времени и уровней экологической организации, так как нельзя выделить какой-то определённый масштаб для описания всего многообразия природных явлений. Соответственно, анализ пространственных взаимоотношений компонентов биоты должен проводиться в различных пространственных масштабах: от микроуровня, определяющегося функционированием микробоценоза в почвенных локусах, к уровню особи (дерева или растения травяно-кустарничкового яруса), взаимодействующей с ближайшими соседями, и далее до взаимоотношений популяций растений напочвенного покрова и древостоя, т.е. на уровне биоценоза.
В последние годы анализ пространственной структуры и пространственной неоднородности экосистем и их биотических компонентов приобретает качественно новый теоретический и практический уровень. Во многом это связано с ускоренным развитием современных технологий наземного и воздушного лазерного 3D‑сканирования, а также аэрофотосъёмки с применением беспилотных летательных аппаратов. Возможность получения подобных наборов измерений, наряду с применением методов математической обработки пространственно распределённых данных, позволяет использовать ранее недоступные подходы к анализу структуры экосистем на разных пространственных уровнях и получать принципиально новую информацию о механизмах внутренней организации, функционирования и устойчивого развития биогеоценозов. Несмотря на прогресс в области анализа пространственных данных, вопросы, на которые можно дать ответ с помощью методов пространственной статистики, остаются в рамках выявления особенностей сформированных структур. Это означает, что появилась возможность вычисления вероятности того, что наблюдаемая структура связана с пространственно-обусловленными явлениями или процессами. Однако методы пространственной статистики не позволяют объяснить механизмы формирования той или иной структуры и то, какие экологические процессы могут быть причиной наблюдаемых паттернов. Необходим подход, объединяющий методы пространственной статистики и индивидуально-ориентированные имитационные модели, которые воспроизводят функционирование и количественные характеристики экосистем, исходя из математического или механистического описания процессов.
Роль живого напочвенного покрова лесных экосистем редко принимается во внимание при анализе углеродного баланса территорий (Goulden et al., 1997; Law et al., 1999). Но во многих широко распространенных типах бореальных лесов сомкнутость древесного полога низкая, что обеспечивает высокую доступность солнечной радиации для растений травяно-кустарничкового яруса и, как следствие, определяет высокую интенсивность фотосинтеза (Baldocchi et al., 2000). Не менее важным является влияние травянисто-кустарничкового яруса на возобновление древесных растений.
Растительный опад в лесных экосистемах играет роль источника питательных веществ, а соотношение темпов его поступления и разложения регулирует скорость динамики питательных веществ в почве и, как следствие, продукционный процесс (Nilsson, Wardle, 2005; Kolari et al., 2006). Следовательно, изменения в структуре растительных сообществ приводят к качественным и количественным изменениям в лесной подстилке, которая, в свою очередь, оказывает непосредственное влияние на накопление углерода в почве (Карпачевский, 1981; Чертов, 1981; Hättenschwiler, Gasser, 2005). Кроме того, характер растительного опада и формируемой им лесной подстилки во многом определяют структуру почвенного микробоценоза, ответственного за процессы трансформации и минерализации органического вещества и соединений азота в почвах.
Анализ структурной сложности лесных экосистем позволяет выявить механизмы и процессы, определяющие их нелинейную динамику и приводящие к формированию специфической пространственной организации лесной растительности. Незаменимым инструментом при проведении подобного анализа является имитационное моделирование, позволяющее формализовать количественное описание динамики элементов лесной экосистемы, пространственных взаимоотношений между элементами и роль взаимодействий между компонентами в поддержании её устойчивости. Под устойчивостью лесной экосистемы в данном случае понимается её способность к поддержанию структуры, функционирования, динамики и продуктивности в процессе развития, как при отсутствии внешних нарушений, так и при разного рода воздействиях. Имитационные эксперименты позволят улучшить понимание комплекса взаимодействий между различными компонентами экосистемы и процессов, определяющих структуру, устойчивость и продуктивность сложных растительных сообществ.
Для отечественной лесной экологии актуальность разработки математических моделей как инструмента прогноза продуктивности и оценки экосистемных функций лесов определяется переходом лесного сектора страны к интенсивной модели развития, ориентированной на более короткие сроки получения товарной продукции, в том числе за счёт более широкого внедрения в практику лесопользования посадок лесных культур и лесных плантаций (Romanov et al., 2016). Помимо вопросов экономической целесообразности затрат на искусственное лесовосстановление и лесоразведение в разных почвенно-климатических условиях, не менее важным становится вопрос обоснования оптимальных лесохозяйственных сценариев, обеспечивающих получение высокой продукции древесины при сохранении экологических функций лесов.
Имитационные модели лесных экосистем, как правило, состоят из следующих блоков: модели возобновления и отмирания деревьев, модели продукции биомассы деревьев, модели конкуренции, модели динамики органического вещества почвы. В них также могут входить модели живого напочвенного покрова, инструменты для имитации лесохозяйственных мероприятий (посадки лесных культур и уход за ними, рубки и т. д.) и различного рода нарушений (пожары, ветровалы, воздействие фитопатогенов). Более подробные обзоры моделей разных типов приводились нами ранее (Грабарник и др., 2019б; Чертов и др., 2019).
Модели возобновления. Одной из важнейших задач анализа динамики лесных экосистем является изучение процессов возобновления. Её решение позволяет приблизиться к пониманию основ устойчивого развития экосистем. Одной из общепринятых концепций динамики лесного ценоза является «оконная» модель (Коротков, 1991; McCarthy, 2001). При этом лесной покров представляется как «мозаика» небольших участков, занятых когортами деревьев, находящихся на разных стадиях развития и сформировавшихся на месте вывалов деревьев предыдущих поколений. В этом случае появление подроста и его развитие до стадии взрослого дерева связано с отпадом деревьев и с расположением соседних крупных деревьев, образующих пространственный «каркас» экосистемы. Эмпирические модели описывают зависимость плотности и видового состава возобновления леса от географических и климатических факторов (Pukkala, Kolström, 1992), а также характеристик местообитания и видового состава верхнего яруса древостоя (Pukkala et al., 2012). Приживаемость деревьев в моделях возобновления рассматривается на локальном уровне в зависимости от наличия ближайших соседей (Kuuluvainen et al., 1993; Fajardo et al., 2006; Wiegand et al., 2009; Pommerening, Grabarnik, 2019). Модели динамических пространственных точечных процессов учитывают конкуренцию между деревьями верхнего яруса, чтобы ответить на фундаментальные вопросы, связанные с динамикой древостоев, и объяснить возникновение пространственных структур (Moeur, 1997).
Модели конкуренции. Конкуренция в индивидуально-ориентированных моделях описывается с разной степенью пространственной детализации. В целом можно выделить несколько основных подходов. В самом общем случае используются индексы конкуренции (Daniels et al., 1986), которые в обобщённом виде описывают силу и направление взаимодействия между растениями в сообществе. Развитием данного подхода является применение в индивидуально-ориентированных моделях теории фитогенного поля для описания конкурентных взаимодействий (Жукова, 2012; Seidl et al., 2012). В ряде моделей два основных вида конкуренции (за свет и за ресурсы почвы) рассматриваются раздельно (или же рассматривается только один из них). При моделировании кроновой конкуренции используются как простые модели, рассматривающие перекрытие т. н. «зон затенения» (фактически — вертикальных проекций крон) соседних деревьев, так и более сложные, использующие трёхмерное представление крон (в дискретных моделях кроны, как правило, аппроксимируются квадратными призмами) и точный расчёт прохождения солнечных лучей через полог (Brunner, 1998; Martens et al., 2000; Stadt, Lieffers, 2000; Olchev et al., 2009; Лебедев, Чумаченко, 2011). В частных случаях кроны могут представляться как плоские «экраны» (Korzukhin, Ter‑Mikaelian, 1995), или в более общем случае модель способна учитывать внутреннюю структуру кроны (неоднородность в распределении биомассы), например, модель Mixfor‑3D (Olchev et al., 2009). Более сложные модели воспроизводят пространственную структуру кроны с высокой точностью (Renshaw, 1985). Среди подобных моделей также заслуживает внимания модель LIGNUM (Perttunen, 2009), которая построена на основе L‑систем и детально воспроизводит архитектуру кроны. Модель LIGNUM предназначена для имитации процессов на уровне отдельных деревьев, но предпринимаются попытки (Sievänen et al., 2008) моделирования роста одновидовых древостоев. Модель PICUS (Lexer, Hönninger, 2001) является индивидуально-ориентированной трёхмерной гэп‑моделью и позволяет учитывать неоднородность лесного полога при расчёте освещённости с помощью трёхмерной модели хода лучей и особенности рельефа. Пространственно-детализированная модель FORRUS‑S (Chumachenko et al., 2003) относится к классу биоэкологических, имитирующих процессы рождения, роста и гибели особей. Модель учитывает влияние условий местообитания и светового режима на ход роста древостоев и позволяет имитировать различные режимы многоцелевого лесопользования, что делает её важным элементом планирования лесохозяйственных мероприятий на лесных участках. В последние годы становится популярным подход, при котором вертикальная структура древостоя упрощается до представления в виде нескольких «слоёв», соответствующим разным ярусам древостоя (например, Колобов, 2013; Collalti et al., 2014).
Для описания пространственной структуры корневых систем предложено несколько регрессионных моделей, описывающих зависимость массы корней от глубины (Strong, LaRoi, 1985; Gale, Grigal, 1987; Starr et al., 2009, 2012). Следует отметить, что модели корневых систем, как правило, не являются самостоятельными, а входят в состав более сложных моделей природных или агроэкосистем. При этом особенно следует подчеркнуть, что даже многие современные имитационные модели вообще не имеют блока, имитирующего конкуренцию за воду и элементы минерального питания (моделируется только конкуренция за свет или используются обобщённые индексы конкуренции). В наиболее простых моделях корневой конкуренции питательные вещества почвы в равных количествах распределяются между всеми растениями на имитируемом участке, а интенсивность поглощения воды и элементов минерального питания убывает с расстоянием от ствола (Yastrebov, 1996; Casper et al., 2003). Многие из упомянутых выше подходов являются попыткой «привязать» интенсивность подземной конкуренции к интенсивности надземной (намного более легко определяемой). Существует также целая группа моделей экосистем, учитывающая лимитирование продуктивности древостоев количеством доступного азота в почве, например iLand (Seidl et al., 2012), PICUS (Lexer, Hönninger, 2001), 4C (Lasch‑Born et al., 2020) и TRIPLEX (Zhou et al., 2008), но в которых почва рассматривается как некий общий ресурс, однородный в пространственном отношении, а прирост биомассы, ограниченный количеством доступного азота, рассчитывается с помощью видоспецифичных функций отклика. Однако целым рядом исследований однозначно показано, что содержание доступных питательных веществ и органического вещества в почвах может отличаться более чем на порядок на удалённости всего в десятки сантиметров (Kuzyakova et al., 1997; Spielvogel et al., 2009).
В имитационных моделях, оперирующих объектами на регулярной решётке, вводится понятие «зоны питания», т. е. области (группы ячеек), занятой корнями конкретного дерева. Обычно в таких моделях масса корней полагается равномерно распределённой по всей площади питания конкретного дерева (Goreaud et al., 2002; Raynaud, Leadley, 2005). Здесь также следует отметить, что лишь немногие из моделей такого рода разработаны для имитации динамики многовидовых древостоев и, соответственно, учитывают видоспецифичные различия в распространении корней (Mao et al., 2015; Shanin et al., 2015a). В системе моделей EFIMOD (Komarov et al., 2003a) используется относительно упрощённое представление процессов конкуренции за свет и минеральный азот в почве и продукции биомассы. Система моделей EFIMOD (Komarov et al., 2003a) учитывает влияние на продуктивность только вышеперечисленных двух факторов. Модель построена на допущении, что все возможные неопределённости будут нивелированы при расчете усреднённой динамики в популяции взаимодействующих особей (Комаров, 2010).
В древостоях, сформированных несколькими видами деревьев с различающимися эколого-ценотическими стратегиями, пространственная неоднородность в доступности ресурсов может быть намного выше, чем в монокультурах (Grime, 2002; Pretzsch, 2014), что является наиболее вероятной причиной более высокой продуктивности многовидовых древостоев по сравнению с одновидовыми насаждениями (Bielak et al., 2014; Cavard et al., 2011; Pretzsch et al., 2015), что подтверждается как экспериментальными исследованиями, так и с помощью имитационного моделирования (Rötzer, 2013; Moghaddam, 2014; Toïgo et al., 2015; Forrester, Bauhus, 2016; Pretzsch, Schütze, 2021). Соответственно, модели конкуренции должны учитывать видоспецифичные особенности развития крон и корневых систем деревьев.
Клеточно-автоматные модели популяций растений. В моделях подобного типа в качестве основного объекта модели выступает индивид, который меняет во времени своё состояние и характеристики по тем или иным правилам, в том числе и в зависимости от состояния и/или размеров соседних объектов (Комаров, 1982; Berger et al., 2008; Herben, Widova, 2012; Oborny et al., 2012, и др.). С помощью данного подхода проводят анализ совместной динамики множества дискретных объектов, имеющих пространственные координаты. Общие свойства моделируемой системы контролируются и определяются через локальные взаимодействия между составляющими систему объектами, и это свойство позволяет строить содержательные модели сложных многокомпонентных систем, таких, как, например, многовидовое сообщество растений, характеризующихся разными экологическими и биологическими свойствами. При этом модели демонстрируют нелинейные свойства, заключающиеся в том, что пространственно-временные модели с простыми правилами развития отдельных особей могут воспроизводить сложные картины популяционной динамики. С помощью клеточно-автоматных моделей, например, изучены эффекты конкуренции и семенного расселения на устойчивость сообществ растений при сильных нарушающих воздействиях (Комаров, 1982; Matsinos, Troumbis, 2002; Komarov et al., 2003b). Клеточные автоматы также применялись для описания процессов инвазии видов с различными способностями к конкуренции за пространство по сравнению с видами локального сообществ (Arii, Parrott, 2006). Объединение техник клеточных автоматов, L-систем и матричного моделирования (Frolov et al., 2015, 2020a, 2020b) позволяет прогнозировать популяционную динамику многовидовых сообществ с учетом видоcпецифичных особенностей роста, развития, реакции на экологические факторы, а также повышает точность масс-балансового подхода к прогнозированию их продуктивности.
Модели динамики органического вещества почвы. В ранних моделях лесных экосистем блоки имитации динамики органического вещества почвы либо отсутствовали, либо были представлены в форме неизменных эдафических условий (Shugart et al., 1992). Пик активной разработки моделей динамики органического вещества почв пришёлся на конец XX века. Модели этого периода часто интегрированы в модели биогеохимических циклов элементов. Из зарубежных моделей наиболее известна модель CENTURY (Parton et al., 1988), из отечественных — рассматриваемые ниже модели ROMUL и Romul_Hum (Chertov et al., 2001; Chertov et al., 2017a, 2017b; Komarov et al., 2017a). Модели VSD+ (Posch, Reinds, 2009) и SMARTml (Bonten et al., 2011) позволяют моделировать динамику небольшого числа почвенных показателей и используются для моделирования отклика наземных экосистем, в том числе лесов, на поступление кислотообразующих и эвтрофирующих соединений с атмосферными осадками. Модель динамики химических свойств лесных почв ForSAFE (Sverdrup et al., 2007) может быть совмещена с моделью растительности напочвенного покрова VEG (Belyazid et al., 2011). Ещё одна группа исследователей из Великобритании продолжает разработки модели MAGIC (Cosby et al., 2001; Oulehle et al., 2012), которая позволяет моделировать изменение кислотно-щелочных свойств почв и внутрипочвенный цикл азота.
По характеру использования моделей органического вещества почв в структуре моделей лесных экосистем они могут быть разделены на две группы. К первой группе относятся системы моделей без «обратной связи», т.е. не учитывающие влияние изменений в почве на продуктивность лесной растительности. Примером таких моделей служат лесоводственные модели хозяйственной продуктивности с пересчётом таксационных параметров в пулы углерода и лесного опада посредством конверсионных функций, как, например, в моделях EFISCEN (Nabuurs et al., 2000) и MELA (Hirvelä et al., 2017). В системах моделей с обратной связью почвенные модели функционально встроены в структуру процессных моделей экосистем (Parton et al., 1988; Chertov et al., 1999; Komarov et al., 2003a; Грабарник и др., 2019а). Основным драйвером обратной связи служит доступный для растений азот почвы, продуцируемый при минерализации органического вещества почвы. В свою очередь, роль азота в продуктивности растений в процессных моделях учитывается либо как как внешний фактор (так же как температура и влажность) по поправочным коэффициентам к базовой функции роста (Kellomäki et al., 1993; Seidl et al., 2012), либо как ресурс, используемый для синтеза биомассы растений (Komarov et al., 2003a; Шанин и др., 2019), по которому рассчитывается прирост биомассы. При этом изменение почвенных запасов органического вещества под влиянием опада растений непосредственно влияет на продукцию доступного азота.
В рамках анализа средствами имитационного моделирования взаимосвязи структуры лесных сообществ и их устойчивого функционирования могут быть сформулированы следующие задачи:
- Математическое описание структуры сложных растительных сообществ на основе современных методов пространственной статистики. Решение этой задачи позволит моделировать особенности пространственной структуры, необходимые для включения в более сложные модели самоорганизации растительного покрова лесных экосистем.
- Построение индивидуально-ориентированных пространственно-детализированных имитационных моделей динамики лесных экосистем. Эти модели должны воспроизводить (а) механизмы конкурентных взаимоотношений за свет и ресурсы почвы, которые определяются пространственной структурой фитоценозов, что позволит получать в имитационных экспериментах реалистичные реконструкции структурных изменений в лесных экосистемах; (б) динамику роста отдельных растений в зависимости от количества полученных ресурсов и условий местообитания. Важным свойством моделей конкуренции должна быть способность имитировать адаптацию растений к неоднородности условий окружающей среды и конкурентному давлению со стороны соседних растений.
- Поиск необходимого уровня детализации описания эндо- и экзогенных процессов, происходящих в лесных экосистемах, что требуется для обеспечения масштабируемости системы моделей.
- Разработка методов моделирования структурно-функциональной организации, популяционной динамики и продуктивности растений живого напочвенного покрова. Решение данной задачи позволит улучшить описание круговорота биофильных элементов с учётом продукции фитомассы растений напочвенного покрова и пространственное варьирование динамики органического вещества почвы как следствие неоднородности структуры живого напочвенного покрова. Данная задача тесно связана с задачей разработки модели естественного возобновления деревьев с учётом пространственной структуры древостоя и напочвенного покрова и формируемых ими условий экотопа.
- Разработка моделей динамики органического вещества почвы (процессов минерализации и гумификации) с учётом пространственной неоднородности в поступлении растительного опада и гидротермического режима почв. Последнее потребует разработки пространственно-детализированной модели почвенного климата, учитывающей факторы его формирования: неоднородность растительности и структуры почвенного покрова с учётом влияния растительности и микрорельефа.
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
Согласно существующим представлениям, пространственная структура лесных экосистем изменяется иерархически, отражая суммарные эффекты влияния разных факторов и многочисленных процессов, лежащих в основе пространственных паттернов того или иного масштаба (Kuuluvainen et al., 1998; Kulha et al., 2018; Тихонова, Тихонов, 2021). При этом некоторые факторы и процессы формируют паттерны в нескольких масштабах (Elkie, Rempel, 2001). Для определения необходимого уровня детализации пространственной неоднородности лесных биогеоценозов, связанной с процессами их функционирования на разных масштабных уровнях, нами был проведён комплекс экспериментальных полевых исследований, результаты которых использованы при модификации и параметризации новой версии системы моделей.
Исследования выполнялись на двух ключевых участках — в Приокско-Террасном государственном природном биосферном заповеднике (юг Московской обл., подзона хвойно-широколиственных лесов) и государственном природном заповеднике «Калужские засеки» (юго-восток Калужской обл., подзона широколиственных лесов). Выбор в качестве объектов исследования лесных сообществ с участием или доминированием широколиственных видов не случаен. В отечественной литературе имеется немало публикаций, связанных с изучением биогенного круговорота и условий функционирования таёжных лесов (Казимиров, Морозова, 1973; Лукина, 1996; Бобкова и др., 2000; Никонов и др., 2002; Коренные …, 2006; Lukina et al., 2019). Данные этих и других публикаций были использованы при разработке первых версий системы моделей EFIMOD (Komarov et al., 2003a) и её последующих модификаций, которые показали хорошее воспроизведение в имитационных оценках особенностей биогенного круговорота углерода в разных типах еловых, сосновых и мелколиственных лесов (Чертов и др., 2015; Komarov, Shanin, 2012). Расширение сферы приложения EFIMOD за счёт включения в подмодели древостоя параметров для широколиственных видов потребовало не только получения количественных данных об особенностях их конкуренции за ресурсы, параметрах роста, распределения биомассы по органам и условий успешного возобновления, но и специального анализа особенностей формирования и динамики пространственной структуры подобных древостоев.
Планируя полевые исследования на ключевых участках, мы исходили из понимания того, что взаимное расположение деревьев разных видов и размеров определяет не только конкуренцию между ними за свет и элементы почвенного питания, но и формирует вариабельность экологических условий под пологом леса, которая, в свою очередь, обеспечивает многообразие экологических ниш разного масштабного уровня, что важно для поддержания продуктивности и экосистемных функций лесов, их биоразнообразия и устойчивого развития. Соответственно, проводя полевые исследования, мы ориентировались, с одной стороны, на ярусно-компонентную структуру лесных биогеоценозов (древостой, подрост, напочвенный покров, лесная подстилка, корнеобитаемые горизонты почв), а с другой, на разномасштабные уровни их проявления и функционирования (сообщество, ценопопуляция, отдельные растения, органы растения).
Краткая характеристика объектов исследования
Постоянная пробная площадь в Приокско-Террасном государственном природном биосферном заповеднике (ППП‑ПТЗ) площадью 1 га (100 × 100 м) заложена в 2016 г. Стороны ППП ориентированы по магнитному меридиану, дополнительно ППП разбита на квадраты 20 × 20 м, углы и центры которых маркированы вешками. В смешанном разновозрастном древостое преобладают Betula spp., Picea abies L. и Pinus sylvestris L., реже встречается Populus tremula L. Во втором ярусе представлены преимущественно Tilia cordata Mill. и Picea abies, реже встречается Quercus robur L. Средний возраст деревьев первого яруса варьирует от 70–75 лет (Tilia cordata, Picea abies) до 110–115 лет (Quercus robur, Pinus sylvestris). Пространственное расположение деревьев разных видов в пределах пробной площади показано на рис. 1. Разреженный характер древостоя в юго-западной части ППП связан с массовой гибелью генеративных деревьев Picea abies в результате повреждения короедом-типографом (Ips typographus (Linnaeus, 1758)) в 2012 г. В подросте преобладают Picea abies и Tilia cordata. На разных участках ППП в травяно-кустарничковом ярусе доминируют Vaccinium myrtillus L., Pteridium aquilinum (L.) Kuhn, Calamagrostis arundinacea Roth и Convallaria majalis L. Почвенный покров относится к дерново-подбурам (Классификация …, 2004) или Albic Luvisol (WRB, 2015). Более детально характеристики почвенно-растительных условий ППП отражены в публикациях (Шанин и др., 2018; Priputina et al., 2020).
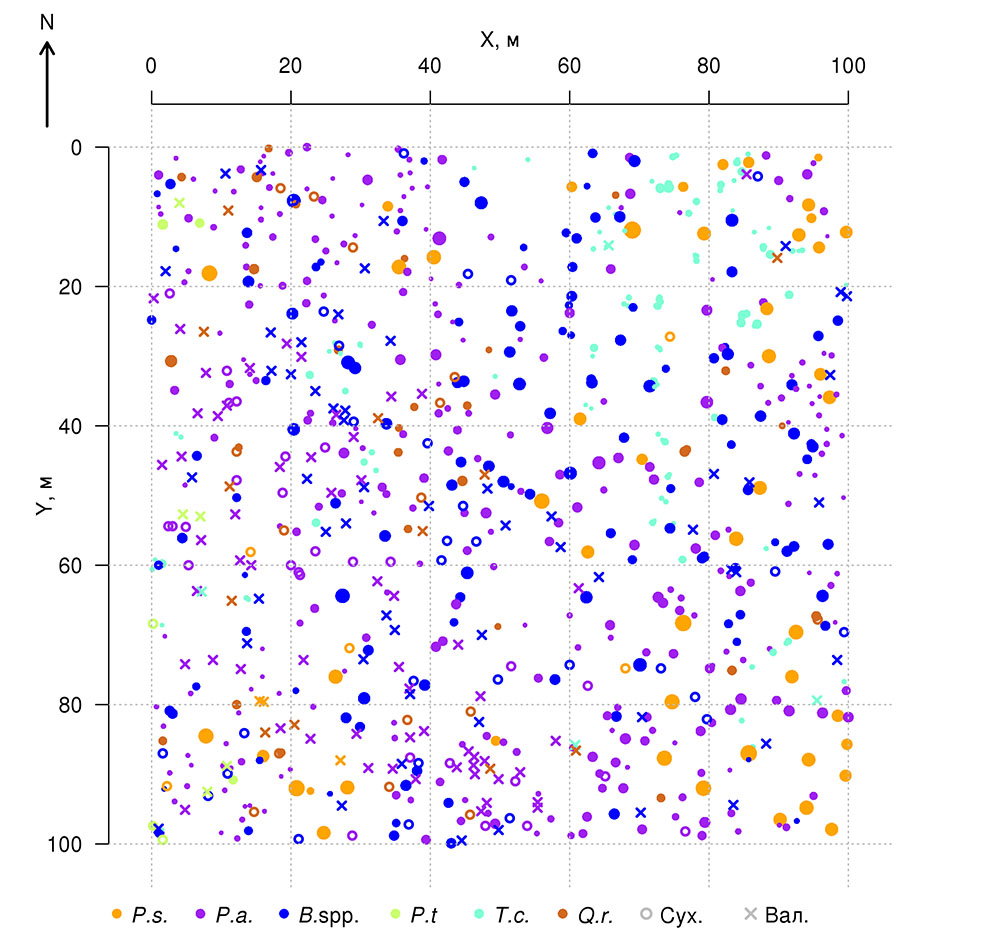
Рисунок 1. План-схема древостоя на ППП‑ПТЗ. P.s. — Pinus sylvestris, P.a. — Picea abies, B.spp. — Betula spp., P.t. — Populus tremula, T.c. — Tilia cordata, Q.r. — Quercus robur, Сух. — сухостойные деревья, Вал. — упавшие с момента первичного учёта 2016 г.
Полевые исследования на ППП-ПТЗ включали следующие тематические блоки в соответствии с компонентной структурой биогеоценозов. Исследования древесного яруса включали в себя:
- Картографирование древостоя, определение онтогенетических состояний и классов Крафта (для живых деревьев), высот, диаметров стволов на уровне груди (DBH) и координат деревьев с помощью лазерного дальномера с функциями измерения высоты и магнитного азимута Laser Technology TruPulse 360B, что позволило подготовить сценарий, необходимый для валидации системы моделей.
- Разносезонная аэрофотосъёмка древостоя с использованием квадрокоптеров с целью создания ортофотопланов ППП‑ПТЗ. Использованы квадрокоптеры фирмы DJI Phantom 4 и Phantom 4 Pro. Полёты выполнялись в автоматическом режиме по сценарию съёмки mosaic flight mode с перекрытием снимков 80–95%.
- Измерение проекций крон деревьев при помощи визуального дешифрирования ортофотопланов, полученных на основе обработки аэрофотоснимков. Работы по пп. 2 и 3 необходимы для параметризации процедеры, описывающей взаимосвязь размерных характеристик ствола и кроны дерева.
- Проведение демографического учёта подроста на 5 учётных площадках (20 × 20 м).
- Анализ распределения в пространстве хвойно-листового и других фракций поверхностного опада 6 видов деревьев (Picea abies, Pinus sylvestris, Betula spp., Quercus robur, Tilia cordata, Acer platanoides) с использованием серий опадоуловителей, установленных на разном удалении от деревьев с учётом их размерных характеристик. На основе полученных данных была проведена параметризация видоспецифичной функции пространственного распределения хвойно-листового опада.
Исследования травяно-кустарничкового яруса включали в себя:
- Разномасштабное пространственное картографирование доминантных видов, оценка проективного покрытия разных видов с учётом сомкнутости древесного полога в местах их произрастания.
- Определение неоднородности условий произрастания ценопопуляций растений в пределах пробной площади: инструментально измерялись показатели освещённости (доступной фотосинтетически активной радиации (ФАР)) и влажности почв, отбирались образцы подгоризонтов (L, F, H) подстилки и гумусово-аккумулятивного горизонта почвы для определения содержания C и N. Эти данные позволили провести валидацию системы моделей с точки зрения приуроченности пространственной структуры живого напочвенного покрова к локальным экологическим условиям.
- Определение условий освещённости под пологом древостоя для разных вариантов проективного покрытия и диапазонов толерантности доминантных видов к факторам освещённости и влажности почв.
- Контролируемый эксперимент по определению зависимости интенсивности фотосинтеза Pteridium aquilinum, Calamagrostis arundinacea и Convallaria majalis от влажности почвы. Полученные по пп. 3 и 4 экспериментальные данные использованы для параметризации видоспецифичных параметров фотосинтеза и функций отклика продуктивности исследуемых видов на влажность корнеобитаемого слоя почвы.
- Отбор образцов доминантных видов с целью получения данных о биомассе, содержании углерода и азота в разных органах вегетирующих растений и растительного опада. На основании этих данных рассчитаны коэффициенты функции ранговых распределений, которые необходимы для вычисления продукционных характеристик подмодели живого напочвенного покрова.
Исследования почв включали в себя:
- Изучение пространственного распределения характеристик органического вещества (Сорг, Nобщ, С:N) лесной подстилки и органоминеральных горизонтов почв в зависимости от расположения деревьев разных видов, сомкнутости крон и видового состава травяно-кустарничкового яруса (ТКЯ).
- Круглогодичный мониторинг температуры и влажности подстилки и органоминеральных горизонтов почв, а также количества атмосферных осадков, поступающих под полог древостоя в зависимости от его сомкнутости и видового состава. Экспериментальные данные, полученные по пп. 1 и 2, использованы для валидации подмоделей гидротермического режима и динамики органического вещества почвы.
Постоянная пробная площадь в государственном природном заповеднике «Калужские засеки» (ППП‑КЗ) располагается в старовозрастном полидоминантном широколиственном лесу без следов рубок и других нарушений на Южном участке заповедника и занимает площадь 10.8 га (200 × 540 м). Пробная площадь заложена в 1986–1988 гг. под руководством проф. О. В. Смирновой; в 2016–2018 гг. проведён повторный перечёт, а в 2021 — повторное картографирование древостоя на участке размером 40 × 40 м. Древостой имеет ярусную структуру и состоит преимущественно из Quercus robur, Fraxinus excelsior L., Tilia cordata, Acer platanoides, Acer campestre L., Ulmus glabra Huds., Betula spp. и Populus tremula. О разнообразии видового состава верхнего яруса древостоя можно судить по аэрофотоснимку, сделанному в осенний период (рис. 2). Возраст отдельных особей Quercus robur — более 300 лет, максимальный возраст деревьев других видов превышает 150 лет (Shashkov et al., 2022). Подлесок сформирован Corylus avellana L., Euonymus europaeus L., E. verrucosus Scop., Lonicera xylosteum L., Prunus padus L.; в подросте представлены преимущественно Tilia cordata, Ulmus glabra, Acer platanoides и Acer campestre. В напочвенном покрове доминируют Aegopodium podagraria L., Asarum europaeum L., Lamium galeobdolon L., Pulmonaria obscura Dumort. и другие неморальные виды. Проективное покрытие растений напочвенного покрова составляет в среднем 65%. Почвенный покров на разных участках пробной площади представлен вариантами дерново-подзолистых, серых и тёмногумусовых почв (Бобровский, Лойко, 2019).

Рисунок 2. Ортофотоплан ППП‑КЗ (по материалам аэрофотосъёмки 10.10.2021; квадрокоптер DJI Phantom 4 Advanced, высота съемки 117 м)
На ППП‑КЗ проводились следующие полевые исследования древесного яруса:
- Разносезонная аэрофотосъёмка древостоя с использованием квадрокоптеров DJI Phantom 4 и DJI Phantom 4 Pro) с целью создания ортофотопланов ППП.
- Картографирование древостоя методом триангуляции, основанном на измерении расстояний между фокальными деревьями (с учётом радиуса их ствола) и опорными точками с известными координатами с помощью лазерного дальномера.
Исследования травяно-кустарничкового яруса предусматривали отбор образцов доминантных видов ТКЯ с целью получения данных о содержании углерода и азота в разных органах вегетирующих растений и в растительном опаде.
Исследования почвенного покрова предусматривали изучение пространственного распределения характеристик органического вещества (Сорг, Nобщ, С:N) лесной подстилки и верхнего органоминерального горизонта почв в зависимости от расположения деревьев разных видов, сомкнутости крон и доминантных видов напочвенного покрова.
Основные результаты полевых исследований
Исследование особенностей пространственной и видовой структуры древесного яруса в многовидовых древостоях
Целью полевых исследований пространственной структуры, видоспецифичных показателей роста и динамики древесного яруса было получение данных, необходимых для модификации подмодели начального размещения деревьев, подмодели конкуренции за фотосинтетически активную радиацию (ФАР) и подмодели продукции биомассы деревьев и её распределения по органам с учётом возможной асимметрии крон. Основной акцент наших исследований сделан на анализе связей пространственных и демографических аспектов динамики лесных древостоев, так как размещение деревьев и их размерные характеристики являются результатом текущих демографических изменений растительного сообщества и экологических процессов, действовавших в прошлом, а конкуренция между деревьями разных онтогенетических состояний и размерных классов является асимметричной.
Полученные в ходе полевых исследований на постоянной пробной площади в Приокско-Террасном заповеднике данные о расположении (координатах) оснований стволов и центроидов проекций крон деревьев верхнего яруса были использованы для анализа характера их пространственного распределения (Шанин и др., 2018), аналогично методике, использованной в более ранних исследованиях (Шанин и др., 2016). Согласно оценкам, распределение в пространстве оснований стволов соответствовало модели случайного размещения, но значение меры согласия с нулевой гипотезой о случайном размещении (p=0.058) было близко к критическому значению 0.05, предполагая, что реальное размещение деревьев имеет пространственные характеристики, отклоняющиеся от таковых для полностью случайного, что может говорить о наличии некоторых признаков равномерности. Дополнительный графический анализ L‑функции показал для исследуемого древостоя низкую встречаемость пар деревьев с расстояниями между основаниями их стволов 4–6 метров, что нетипично для случайного размещения. Анализ распределения в пространстве центроидов (геометрических центров) проекций крон показал, что их расположение, напротив, значимо отличалось от случайного в сторону более регулярного (p=0.032). Отклонение от случайного размещения было связано с незначительным вкладом в суммарное распределение пар коротких расстояний (1.5–2.5 м). Показанная для исследуемого древостоя регулярность расположения в пространстве центроидов проекций крон при случайном расположении оснований стволов, отмечавшаяся и в других работах (Секретенко, 2001; Schröter et al., 2012), отражает механизм адаптации деревьев к конкуренции со стороны соседей, который проявляется в асимметричном горизонтальном росте крон в разных направлениях. У деревьев с разными стратегиями роста величина асимметрии проявляется по‑разному: она выше у реактивных и толерантных видов, ниже — у конкурентных, что предполагает необходимость соответствующей видоспецифичной параметризации в модели. Следует отметить, что благодаря данному адаптационному механизму многовидовой древостой способен поддерживать высокий уровень продукции фитомассы, максимально используя имеющиеся ресурсы.
Выполненные в ходе полевых исследований измерения площадей проекций крон деревьев показали их разрастание в направлении открытых участков (рис. 3), которые образованы разрывами («окнами») в лесном пологе в результате вывалов деревьев первого яруса. Этот факт и то, что с образованием ветровальных окон связана пространственная неоднородность экологических условий под пологом леса (Восточноевропейские леса …, 2004; Бобровский, 2010), определили наше внимание к проблеме изучения пространственных особенностей расположения и оценки площади ветровальных окон в разновозрастных древостоях сложного видового состава.
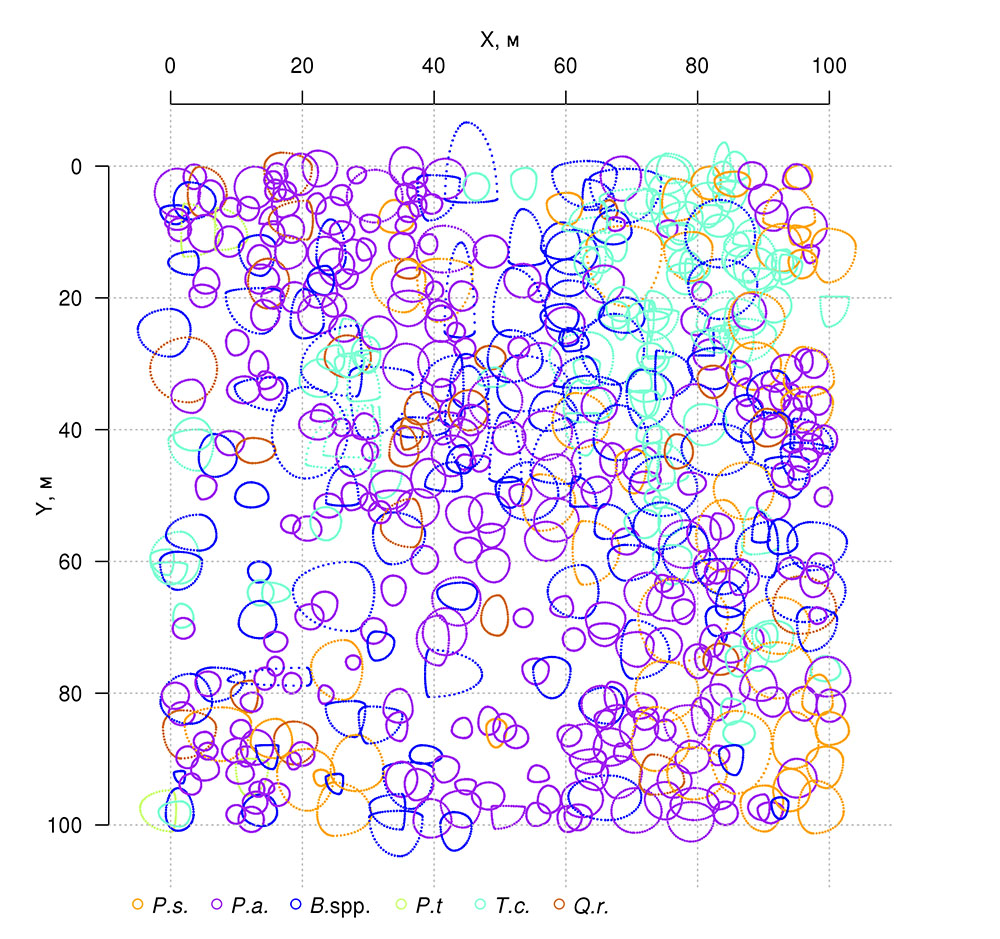
Рисунок 3. План-схема проекций крон деревьев на ППП‑ПТЗ. Цветом показаны следующие виды: P.s. — Pinus sylvestris, P.a. — Picea abies, B.spp. — Betula spp., P.t. — Populus tremula, T.c. — Tilia cordata, Q.r. — Quercus robur
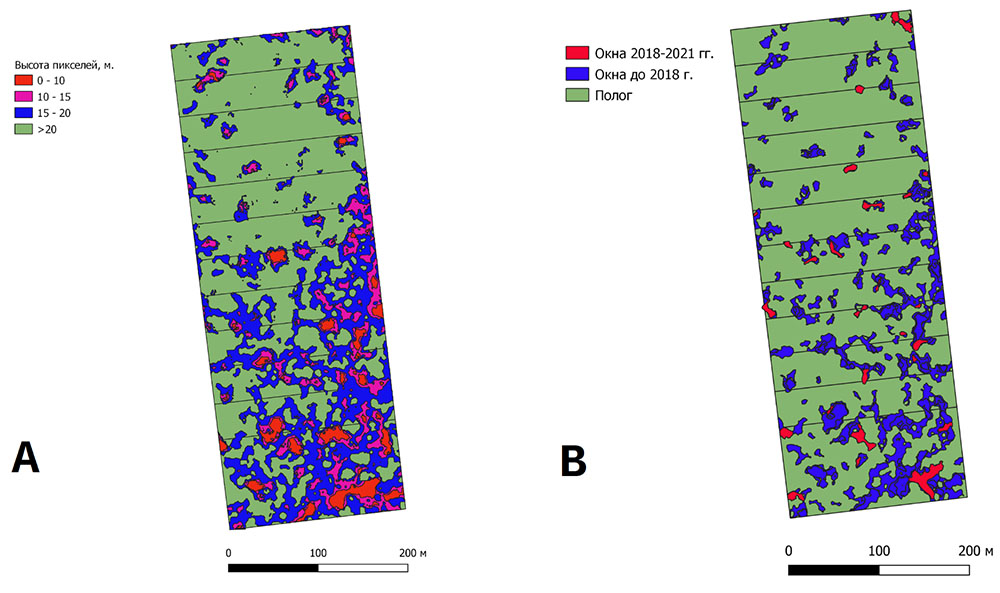
По результатам аэрофотосъёмки постоянной пробной площади в заповеднике «Калужские засеки» был выполнен анализ распределения высот поверхности полога древостоя, позволивший выделить, определить размеры и оценить долю ветровальных окон разного возраста в древесном пологе (рис. 4).
Полевые исследования на ППП в заповеднике «Калужские засеки» включали также проведение повторного перечёта древостоя, что позволило получить данные о динамике основных характеристик древостоя за 30‑летний период (с 1988 по 2018 гг.). Результаты сравнительного анализа показали заметное увеличение среднего диаметра деревьев светолюбивых видов (Quercus robur, Fraxinus excelsior, Populus tremula и Betula spp.). У теневыносливых видов (Ulmus glabra, Tilia cordata, Acer platanoides) за тот же отрезок времени средний диаметр возрос незначительно или даже уменьшился, но увеличилось общее число деревьев этих видов, что свидетельствовало об их успешном возобновлении под пологом в условиях относительной ограниченности ресурсов ФАР. Полученные данные являются важными для анализа и интерпретации результатов имитационных оценок, а также валидации системы моделей на качественном уровне.
Изучение пространственного распределения поверхностного опада разных видов деревьев
Особенности распределения хвойно-листового и других фракций опада в пространстве лесного биогеоценоза являются важным фактором формирования неоднородности (мозаики) почвенных условий (Орлова и др., 2011). Для параметризации функции, используемой в разрабатываемой системе моделей для описания пространственного распределения хвойно-листового опада древесного яруса, на ключевом участке в Приокско-Террасном заповеднике были установлены 12 серий опадоуловителей с площадью сбора 0.25 м2 (0.5 × 0.5 м) под деревьями видов Pinus sylvestris, Picea abies, Betula spp., Quercus robur, Tilia cordata, Acer platanoides (по 2 серии на каждый вид). Для установки опадоуловителей выбирали деревья, расстояние от которых до ближайшего дерева того же вида составляло не менее 100% высоты наиболее высокого из деревьев (либо фокального, либо наиболее высокого из соседних деревьев того же вида). Каждую серию из 5 опадоуловителей устанавливали по направленной от фокального дерева трансекте на расстоянии, соответствующем 0.050, 0.125, 0.250, 0.500 и 1.000 высоты фокального дерева. С помощью угломерной съёмки фиксировали расположение всех деревьев, проекции крон которых перекрывают трансекту. Опад отбирали один раз в месяц. Опад фокального дерева сортировали на фракции: листва или хвоя; ветви и кора; прочее (семена, шишки, почечные чешуи и др.). Опад деревьев других видов не разделялся по фракциям. Анализ полученных данных о пространственном распределении хвойно-листового опада (рис. 5) показал, что основная масса опада, поступающего на поверхность почвы, аккумулируется на расстоянии до 0.125–0.250 высоты соответствующего дерева. Характер его распределения определяется свойствами листьев и хвои деревьев разных видов, в первую очередь их удельной массой. Среди исследуемых видов наибольшая относительная дальность разлёта характерна для Betula spp., наименьшая — для Picea abies. В распределении остальных фракций опада выраженных закономерностей не выявлено.
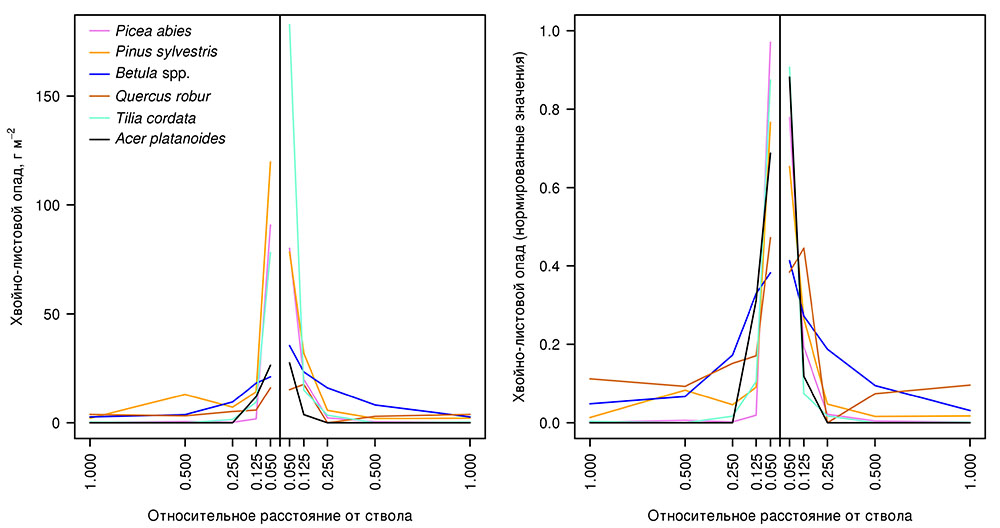
Рисунок 5. Пространственное распределение хвойно-листового опада деревьев разных видов: слева — в абсолютных единицах; справа — значения, нормированные относительно суммарного количества опада для всей трансекты
Исследования динамики подроста и возобновления древесных видов
Демографическое исследование подроста (деревьев с диаметром ствола менее 6 см) проводилось в Приокско-Террасном заповеднике на 5 учётных площадках размером 20 × 20 м, заложенных в пределах ППП. Получены количественные данные, показывающие преобладание в составе подроста позднесукцессионных видов Tilia cordata, Quercus robur, Picea abies и присутствие в небольшом количестве Acer platanoides. Раннесукцессионные виды Pinus sylvestris и Betula spp. были представлены лишь ювенильными и имматурными особями, а подрост Populus tremula не обнаружен, несмотря на присутствие генеративных деревьев этого вида в верхнем ярусе древостоя. Полученные для ППП‑ПТЗ результаты отражают особенности характерной для подзоны хвойно-широколиственных лесов стадии сукцессионного развития древостоя (после рубок или сильных пожаров), когда в нём происходит смена раннесукцессионных видов позднесукцессионными (Сукцессионные процессы …, 1999). Анализ таблиц сопряжённости (Vergarechea et al., 2019) показал, что подрост Tilia cordata мало представлен на участках с доминированием в древостое Betula spp. и Calamagrostis arundinacea и Pteridium aquilinum в напочвенном покрове. Для Picea abies и Quercus robur такие условия, напротив, благоприятны. Вместе с тем подрост Picea abies и Quercus robur мало представлен на участках с доминированием в пологе Pinus sylvestris и Convallaria majalis — в живом напочвенном покрове, тогда как для развития подроста Tilia cordata такие условия благоприятны. На участках с доминированием в пологе Betula spp. и доминированием в живом напочвенном покрове Vaccinium myrtillus L. мало представлен подрост Quercus robur.
Исследование условий произрастания, видовой, пространственной структуры и динамики травяно-кустарничкового яруса лесных сообществ
Целью исследований было получение экспериментальных данных, необходимых для уточнения алгоритмов и параметризации подмодели живого напочвенного покрова, позволяющей моделировать структурно-функциональную организацию и популяционную динамику растений напочвенного покрова, а также их вклад в биогенный круговорот элементов в лесных экосистемах. Основная часть исследований этого тематического блока выполнялась на территории Приокско-Террасного заповедника и в его окрестностях; объектами изучения были доминантные виды травяно-кустарничкового яруса хвойно-широколиственных и широколиственных лесов.
Определение диапазонов толерантности видов к факторам освещённости и влажности почв
Объекты исследования — Aegopodium podagraria, Calamagrostis arundinacea, Carex pilosa L., Convallaria majalis, Oxalis acetosella L., Pteridium aquilinum, Vaccinium myrtillus, Vaccinium vitis—idaea L. Для оценки диапазонов толерантности растений по освещённости (таблица 1) для ценопопуляции (ЦП) каждого из видов были заложены временные пробные площади (ПП) в крайних по освещённости условиях. Пропускание солнечной радиации пологом леса (Global Light Index, GLI) определялось на уровне фотосинтезирующих органов растений. Были сделаны циркулярные полусферические фотографии в зенит с помощью фотоаппарата Canon EOS 600D с объективом Sigma AF 4.5/2.8 EX DC HSM Fisheye, угол обзора которого равен 180 градусов. Верх кадра ориентировался на истинный север с учётом магнитного склонения.
Для определения диапазонов толерантности растений по влажности почвы (таблица 1), для ЦП каждого из видов были заложены ПП в крайних по влажности условиях. Измерения влажности проводились многократно в разных погодных условиях. Данные о влажности почв получены почвенным влагомером МГ‑44 с 4‑электродным датчиком (не менее 15 измерений для каждой ПП в каждый срок измерений).
Таблица 1. Диапазоны толерантности видов растений травяно-кустарничкового яруса к факторам освещённости и влажности почв
| Вид | Диапазон толерантности к влажности подстилки (об. %) | Диапазон толерантности к освещённости (GLI, %) |
| Aegopodium podagraria | 5.2–25.3 | 0.3–10.3 |
| Calamagrostis arundinacea | 1.5–29.3 | 1.1–22.4 |
| Carex pilosa | 7.4–26.9 | 0.4–28.6 |
| Convallaria majalis | 5.3–33.7 | 0.9–24.0 |
| Oxalis acetosella | 7.2–29.9 | 0.3–8.6 |
| Pteridium aquilinum | 3.2–24.8 | 2.1–30.9 |
| Vaccinium myrtillus | 5.7–61.1 | 0.4–27.5 |
| Vaccinium vitis—idaea | 4.9–46.8 | 0.4–31.9 |
Определение влияния мозаики условий, создаваемой стволами и кронами деревьев разных видов, на влажность почвы и освещённость на уровне ТКЯ
Для ценопопуляций Calamagrostis arundinacea, Convallaria majalis, Pteridium aquilinum, Vaccinium myrtillus, Vaccinium vitis‑idaea были заложены по 5 микросайтов вдоль трансект от ствола одного дерева до ствола соседнего с ним дерева (2 в прикомлевой части, 2 под кронами деревьев и 1 в межкроновом пространстве). На каждом из микросайтов выполнены измерения влажности почв и оценки пропускания солнечной радиации пологом леса (рис. 6). На этих же микросайтах взяты образцы лесной подстилки и верхнего корнеобитаемого слоя почвы для определения в них содержания азота и углерода.

Рисунок 6. Снимки пропускания света кронами разной плотности (А — разреженные, Б — средней плотности, В — плотные)
Определение зависимости интенсивности фотосинтеза от влажности почвы в контролируемом эксперименте
Исследования проводились на временной пробной площади размером 1 × 1 м, где совместно произрастали Pteridium aquilinum, Calamagrostis arundinacea, Convallaria majalis. За неделю до начала эксперимента на ПП были установлены регистраторы влажности WatchDog с двумя датчиками влажности WaterScout SM-300 (1 в лесной подстилке и 1 в минеральном горизонте на глубине 5 см от нижней границы подстилки). Дополнительно были установлены датчики температуры (на поверхности почвы, в подстилке и в минеральной почве на глубинах 10 и 20 см). 12 августа 2019 г. в период с 10:00 до 11:30 часов на ПП было внесено 212 литров воды, что примерно соответствовало норме осадков за 3 летних месяца для данной территории. Для предотвращения дополнительного увлажнения ПП в ходе эксперимента, площадка была накрыта тентом, закреплённым на высоте 1.5 м. На растениях каждого из видов были выбраны по 3 листа (т. е. 9 точек измерения), и в течение суток (с 11:30 12.08.2019 по 11:30 13.08.2019) проводились измерения интенсивности фотосинтеза в каждой из 9 точек по очереди без перерывов между измерениями (по окончании цикла измерений он повторялся). Показатели фотосинтеза определялись флуориметром PAR-FluorPen FP 110D. Показания датчиков влажности почвы регистрировались автоматически с интервалом 15 минут, температурных датчиков — в ручном режиме с интервалом в 1 час. Параллельно каждый час фиксировалась температура и влажность воздуха с помощью аспирационного психрометра. После суточного цикла измерений разовые измерения в 9 точках повторялись каждые 3 дня до окончания вегетационного периода по аналогичной методике.
Дополнительно на нескольких ПП выполнено определение параметров функции отклика интенсивности фотосинтеза доминирующих видов травяно-кустарничкового яруса на изменение температуры воздуха и влажности лесной подстилки и корнеобитаемого слоя почв (рис. 7). Показатели фотосинтеза определялись на ПП в течение вегетационных сезонов 2018–2021 гг. при разных условиях температуры и влажности почвы. Выполнено более 3000 измерений. Влажность корнеобитаемого слоя определялась почвенным влагомером с предварительной градуировкой для почв, различающихся по гранулометрическому составу. На каждой ПП единовременные измерения выполнялись в 15-кратной повторности, что обусловлено большой вариативностью этого показателя. Температура измерялась в диапазоне условий от −2º С до +27º С (прибор IT-8) для воздуха один раз в один цикл исследований для каждой ПП, для почвы в трёхкратной повторности.
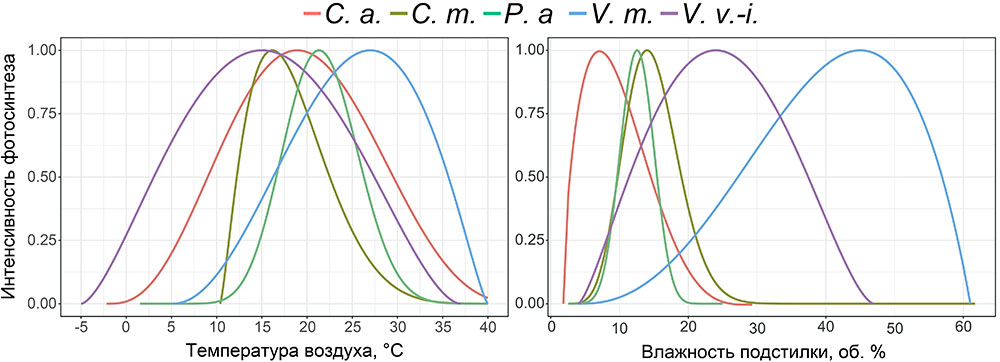
Рисунок 7. Функции отклика интенсивности фотосинтеза доминирующих видов травяно-кустарничкового яруса на изменение температуры воздуха и влажности лесной подстилки. C. a. — Calamagrostis arundinacea, C. m. — Convallaria majalis, P. a. — Pteridium aquilinum, V. m. — Vaccinium myrtillus, V. v.-i. — Vaccinium vitis‑idaea
Исследования динамики роста и развития растений в ходе онтогенеза
Объектами изучения были Aegopodium podagraria, Calamagrostis arundinacea, Carex pilosa, Convallaria majalis, Oxalis acetosella, Pteridium aquilinum. Пробные площади были заложены в 2018–2020 гг. на участках с доминированием этих видов. Проведено картографирование растений Calamagrostis arundinacea (54 шт.), парциальных кустов Carex pilosa (20 шт.) и подземных побегов длиннокорневищных растений Aegopodium podagraria (10 шт.), Convallaria majalis (15 шт.), Oxalis acetosella (15 шт), Pteridium aquilinum (20 шт.) для исследования роста корневищ. Фрагменты подземных побегов Oxalis acetosella с живыми листьями окольцовывали тонкой металлической проволокой с оранжевыми пластиковыми бирками с номерами. Побеги остальных растений замечали синими пластиковыми бирками, воткнутыми рядом с побегом в землю. Дважды — весной и осенью — у изучаемых растений измерялись: длина междоузлий на побеге, число почек, число листьев, для каждого листа — длина черешка листа, размер горизонтальной проекции поверхности каждой листовой пластины на поверхность земли в двух перпендикулярных направлениях. Для Oxalis acetosella дополнительно отмечалось число цветоносных бутонов на побеге. Побеги зарисовывали. Так как у Carex pilosa листья сохраняют жизнеспособность и в зимний период, для выяснения сроков их отмирания была разработана специальная методика. Из укрывного материала были вырезаны квадраты со стороной 30 см, что соответствует размеру надземной части парциальных кустов Carex pilosa. В центре квадратов были сделаны отверстия диаметром 10 см. Полученный «фартук» надевался на парциальный куст и закреплялся на земле по четырём сторонам синими пластиковыми бирками с номерами. В каждый срок наблюдений для каждого парциального куста подсчитывали число вегетативных и генеративных побегов, число живых листьев, число отмерших листьев; у живых листьев измеряли длину целиком и живую часть листа. Подсчитывали число генеративных побегов. Дополнительно были измерены и зарисованы фрагменты всех растений, выкопанные для расчёта ранговых распределений по органам.
Определение аллометрических соотношений органов растений
Для расчёта аллометрических соотношений были отобраны растения видов Aegopodium podagraria, Calamagrostis arundinacea, Carex pilosa, Convallaria majalis, Oxalis acetosella, Pteridium aquilinum. Особи Calamagrostis arundinacea (20 экземпляров) отбирались целиком. Для Aegopodium podagraria, Carex pilosa, Convallaria majalis, Oxalis acetosella отбирали фрагменты растений на микросайтах размером 0.25 м2 (по 12–25 микросайтов на каждый вид). Для Pteridium aquilinum были выкопаны 24 фрагмента растений на участке размером 0.5 × 1.5 м, а также растение целиком с площади 0.5 × 8.0 м (рис. 8). Корневые системы всех растений максимально бережно выкапывали из почвы, после чего корни отмывали в проточной воде. В лаборатории все фрагменты растений были измерены и зарисованы, а затем разделены на органы, которые после высушивания до абсолютно сухого состояния были взвешены.
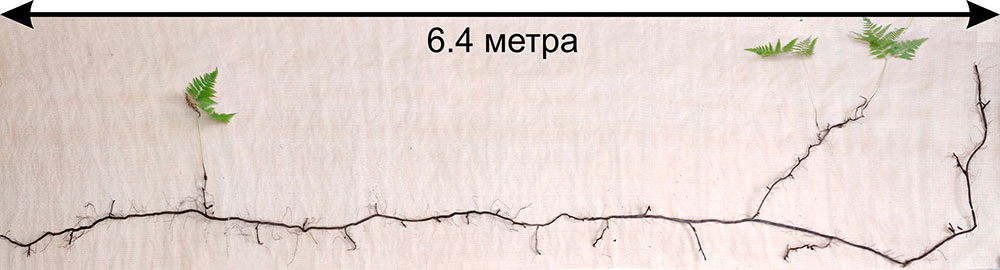
Рисунок 8. Определение размеров корневищ Pteridium aquilinum
Определение содержания азота в органах растений и корнеобитаемых горизонтах почв
Параллельно с определением аллометрических соотношений, в образцах фитомассы разных органов растений было определено содержание углерода и азота (методом высокотемпературного сжигания образцов в CHN-анализаторе). Одновременно с растениями на участках их произрастания были отобраны пробы лесной подстилки и соответствующего исследуемым видам корнеобитаемого слоя минеральной почвы, в которых также проведено определение содержания углерода и азота.
Исследования пространственной неоднородности почвенных условий под пологом леса
Мониторинг температуры и влажности лесной подстилки и верхних минеральных горизонтов почвы и количества атмосферных осадков как показателей микроклиматических условий под пологом леса
Круглогодичное измерение температуры (Т) лесной подстилки и верхних минеральных горизонтов почвы проводилось, начиная с 11.11.2016, при помощи двухканальных регистраторов температуры EClerk-USB-2Pt-Kl (производство «Рэлсиб», диапазон измерений: −50… +200 °С, точность: ±0.5 °С). Температура регистрировалась с периодичностью 1 раз в час датчиками, расположенными на границе подстилки и органоминерального горизонта почвы и в почве на глубине 10 см. С целью оценить влияние крон разных видов деревьев на затенение поверхности почвы, регистраторы установлены сериями для пар деревьев «Picea abies — Pinus sylvestris», «Pinus sylvestris — Pinus sylvestris», «Picea abies — Picea abies», «Pinus sylvestris — Betula spp.» и «Betula spp. — Picea abies» по 5 датчиков в каждой серии (2 в прикомлевой части деревьев, 2 под кронами, 1 в межкроновом пространстве). Измерение влажности проводилось на трёх из пяти серий: «Picea abies — Pinus sylvestris», «Pinus sylvestris — Betula spp.» и «Betula spp. — Picea abies»; на них же в течение тёплого сезона проводилось измерение количества осадков. Регистрация осадков и влажности почвы, начатая 28.08.2018, производилась автоматическими регистраторами WatchDog 1400 c дождемерами Watchdog Tipping Bucket Rain Gauge и датчиками влажности почвы WaterScout SM 100 (Spectrum Technologies Inc., США). Датчики влажности установлены в подстилке и горизонтах почвы на глубинах 5 и 15 см от нижней границы подстилки. При анализе результатов измерений гидротермических показателей центральная точка каждой серии (в межкроновом пространстве) была принята за базовую, для остальных четырёх точек рассчитывалась разность показателей с базовой точкой. Результаты анализа данных по распределению температуры (Т) на границе между подстилкой и органоминеральным горизонтом не показали заметных отклонений Т под кронами и возле комля от Т в межкроновом пространстве. Для Т почвы на глубине 10 см в тёплый период года под Picea abies наблюдалось относительное понижение по сравнению с межкроновым пространством. Кроме того, влажность подстилки под кронами Picea abies в среднем была ниже, а под кронами Pinus sylvestris — выше, чем на участках между кронами (рис. 9). В минеральной почве на глубинах 5 и 15 см эти тенденции отсутствовали. Данные мониторинга почвенных гидротермических условий подтверждают важность учёта в подмодели динамики органического вещества почвы локального размещения деревьев разных видов через поправочные коэффициенты зависимости разложения видоспецифичного опада от влажности подстилки.
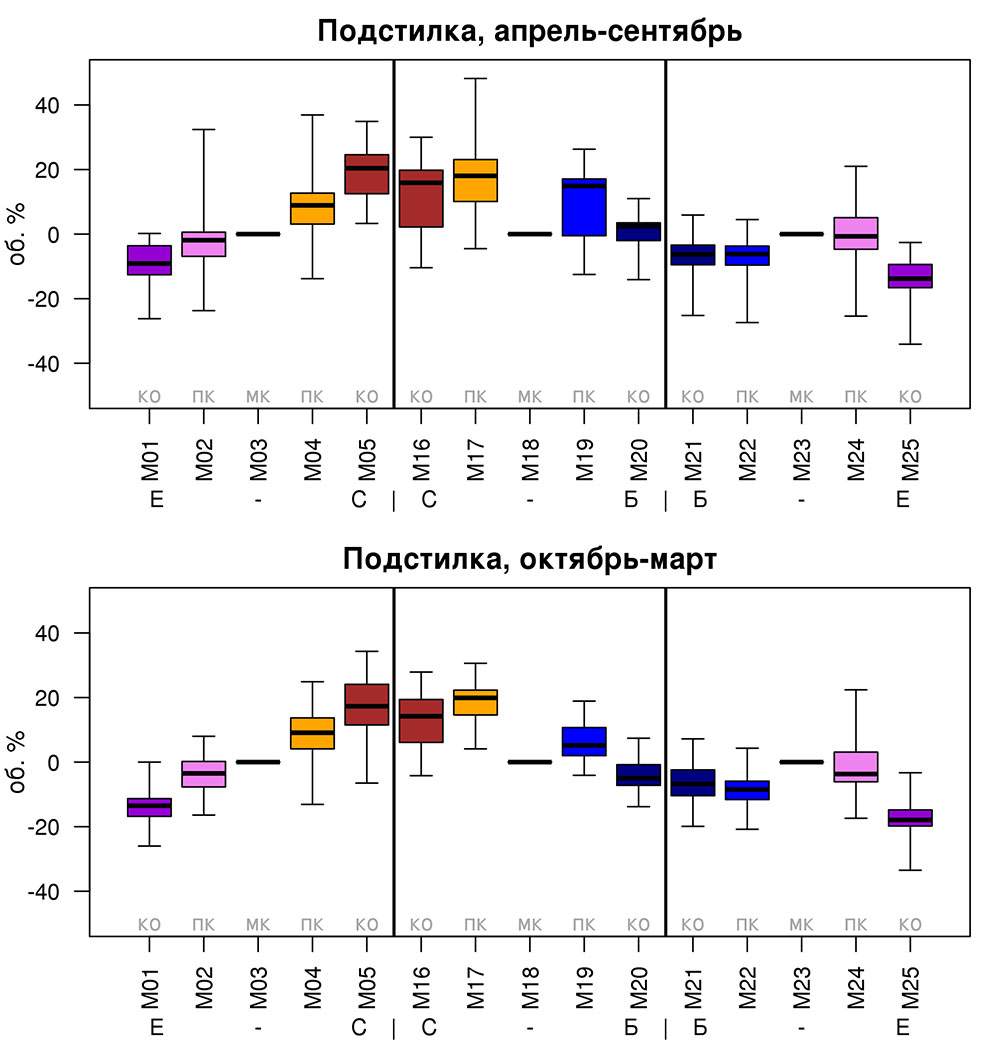
Рисунок 9. Вариация отклонений влажности подстилки под деревьями (КО — у комля, ПК — под кроной) от межкроновых участков (МК) в тёплый и холодный периоды года. Е — Picea abies, С — Pinus sylvestris, Б — Betula spp. Показаны медиана (толстая горизонтальная линия), 1-й и 3-й квартили («боксы») и размах («усы»)
Анализ пространственной неоднородности характеристик органического вещества (Сорг и Nобщ) в почвах в зависимости от видовой структуры древесного яруса и напочвенного покрова
Почвенные исследования проводились по единой методике в августе 2018 г. на ключевых участках в заповеднике «Калужские засеки» (ППП‑КЗ) и Приокско-Террасном заповеднике (ППП-ПТЗ). С целью учёта влияния доминирующих видов древесного яруса и напочвенного покрова на распределение органического вещества в почвах, пробы лесной подстилки (О) и гумусового (AY) горизонтов отбирались по трансектам между двумя соседними деревьями сериями из 5 точек (аналогично мониторингу гидротермических условий и геоботаническим исследованиям). На ППП-КЗ с учётом многовидового состава древостоя было заложено 10 трансект для пар деревьев «Tilia cordata — Quercus robur», «Tilia cordata — Betula spp.», «Tilia cordata — Populus tremula», «Tilia cordata — Acer platanoides», «Quercus robur — Acer platanoides», «Quercus robur — Populus tremula», «Quercus robur — Fraxinus excelsior», «Fraxinus excelsior — Acer platanoides», «Fraxinus excelsior — Betula spp.», «Ulmus glabra — Ulmus glabra». На ППП‑ПТЗ было выбрано 7 трансект с разным сочетанием пар преобладающих видов деревьев первого яруса: Pinus sylvestris, Picea abies и Betula spp. На ППП‑ПТЗ при отборе проб фиксировалась мощность лесной подстилки (см); на ППП‑КЗ мощность подстилки на момент отбора проб во всех точках не превышала 1 см. Результаты исследований частично опубликованы (Priputina et al., 2020).
Для почвенного покрова в сообществе смешанного хвойно-широколиственного леса (ППП‑ПТЗ) показано возрастание мощности лесной подстилки от межкроновых пространств к подкроновым и прикомлевым участкам, что отражает интенсивность поступления хвойно-листового опада, подтверждённое данными опадоуловителей. Содержание Сорг и Nобщ в горизонте О варьировало в диапазонах 17.6–44.9 и 0.84–1.79%, а в горизонте AY — 0.71–8.5 (Сорг) и 0.035–0.33% (Nобщ). Более высокое варьирование показателей было характерно для горизонта AY, в т. ч. в пробах из межкроновых пространств прослеживалась связь между содержанием Nобщ в почве и азотным статусом доминирующих видов травяно-кустарничкового яруса. В почве полидоминантного древостоя широколиственного леса (ППП‑КЗ) содержание Сорг в горизонте О в среднем составляло 25–30%; повышенные значения Сорг (40–45%) были под кронами Betula spp. и Ulmus glabra, а минимальные — под кронами Tilia cordata (20%). Кроме того, для горизонта О межкроновых участков была показана повышенная вариабельность значений Сорг. В горизонте AY содержание Сорг составило 1.3–3.5%. Для Quercus robur, Tilia cordata и Fraxinus excelsior значения содержания Сорг в гумусовом горизонте под кронами были ниже, чем в приствольных участках, для остальных видов деревьев такой закономерности не наблюдалось. Содержание Nобщ в горизонте О в среднем составляло 1.0–1.5%, в горизонте AY — 0.15–0.20%. Варьирование содержания Nобщ в почве ППП-КЗ было заметно ниже, чем для ППП-ПТЗ. Выявленные в ходе почвенных исследований связи содержания Сорг и Nобщ в почвах с характером растительного покрова древесного и травяно-кустарничкового ярусов отражают особенности пространственной локализации и качественных характеристик поверхностного и внутрипочвенного опада и условий его трансформации под влиянием гидротермических условий, формирующихся под пологом леса (Dhiedt et al., 2022).
КРАТКОЕ ОПИСАНИЕ СИСТЕМЫ МОДЕЛЕЙ
Система моделей EFIMOD3 реализована на языке статистического программирования R v. 4.1.3 (R Core Team, 2014) и включает в себя следующие основные блоки (подмодели): подмодель начальной инициализации микрорельефа, подмодель начального размещения деревьев, подмодели конкуренции за фотосинтетически активную радиацию (ФАР) и азот почвы в доступных для растений формах, подмодель продукции биомассы деревьев и её распределения по органам, подмодель пространственного распределения напочвенного и внутрипочвенного растительного опада и стволового опада, подмодель динамики органического вещества почвы, подмодель гидротермических условий в почве и подмодель динамики травяно-кустарничкового яруса.
Система моделей функционирует с годичным шагом (внутренний шаг отдельных подмоделей или отдельных процедур может быть более подробным, месячным, суточным или часовым; в данном случае речь идёт о дискретности во времени, с которой рассчитываются выходные параметры состояния) на квадратной имитационной площадке, разделённой на квадратные ячейки (далее по тексту также называется «имитационной решёткой» или «имитируемым участком»). Максимальный размер имитационной решётки составляет 100 × 100 м (1 га); размер ячейки может быть произвольным и в большинстве последующих имитационных экспериментов с системой моделей был принят равным 0.5 × 0.5 м. Во избежание краевого эффекта используется приём замыкания на тор, предполагающий, что ячейки, расположенные на краю имитируемого участка и не имеющие соседей с одной или двух сторон, используют ячейки с противоположного края в качестве соседей (Haefner et al., 1991). Общая схема системы моделей представлена на рис. 10. Краткое описание алгоритмов подмоделей приведено ниже, более детальное описание алгоритмов, а также описания процедур параметризации, валидации и анализа чувствительности подмоделей приведены в цитируемых ниже публикациях. Список параметров системы моделей приведён в таблицах 2–5.
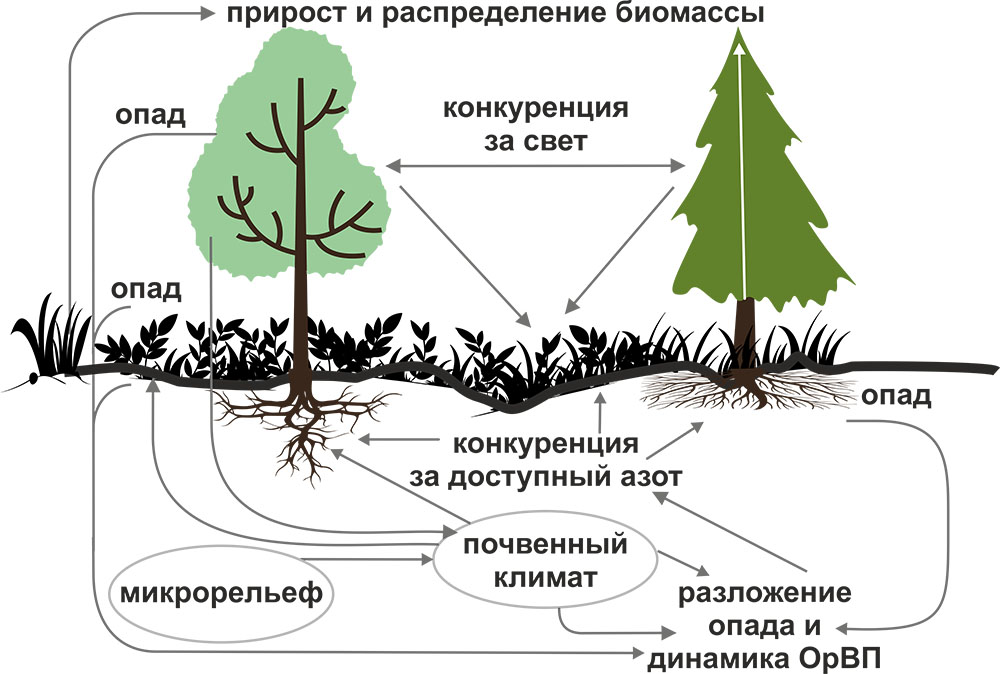
Рисунок 10. Общая схема системы моделей
Таблица 2. Видоспецифичные параметры подмодели конкуренции за минеральный азот почвы (воспроизведено по (Shanin et al., 2015a), с изменениями и дополнениями)
| Ps | Pa | Ls | As | Bp | Pt | Qr | Tc | Fs | Ap | Ug | Fe | |
| aavg | 13.30 | 9.01 | 9.04 | 13.42 | 15.57 | 14.72 | 8.31 | 9.86 | 9.64 | 8.42 | 10.75 | 12.21 |
| bavg | 4.50 | 4.51 | 4.69 | 4.37 | 8.01 | 6.22 | 18.74 | 12.44 | 19.42 | 5.67 | 6.04 | 5.02 |
| cavg | 0.060 | 0.160 | 0.155 | 0.072 | 0.095 | 0.110 | 0.141 | 0.088 | 0.078 | 0.091 | 0.064 | 0.102 |
| amax | 14.84 | 11.99 | 12.02 | 15.50 | 22.11 | 18.05 | 10.24 | 12.71 | 10.98 | 10.26 | 13.24 | 14.02 |
| bmax | 2.77 | 3.13 | 3.22 | 2.84 | 6.64 | 5.22 | 9.76 | 7.78 | 12.62 | 3.54 | 3.62 | 3.78 |
| cmax | 0.068 | 0.190 | 0.186 | 0.081 | 0.110 | 0.140 | 0.153 | 0.094 | 0.080 | 0.092 | 0.068 | 0.112 |
| FRff | 0.033 | 0.050 | 0.039 | 0.048 | 0.029 | 0.031 | 0.034 | 0.032 | 0.027 | 0.034 | 0.048 | 0.026 |
| SRff | 0.036 | 0.053 | 0.041 | 0.051 | 0.031 | 0.029 | 0.036 | 0.034 | 0.028 | 0.035 | 0.050 | 0.03 |
| mstrat | 0.8 | 1.4 | 1.1 | 1.1 | 1.2 | 1.2 | 0.9 | 1.0 | 1.2 | 1.0 | 1.0 | 0.9 |
| aur | 0.226 | 0.108 | 0.215 | 0.122 | 0.138 | 0.119 | 0.101 | 0.097 | 0.112 | 0.161 | 0.115 | 0.140 |
| bur | 0.023 | 0.022 | 0.024 | 0.022 | 0.021 | 0.021 | 0.020 | 0.020 | 0.020 | 0.020 | 0.020 | 0.021 |
Примечание: Ps — Pinus sylvestris, Pa — Picea abies, Ls — Larix sibirica, As — Abies sibirica, Bp — Betula pendula Roth / Betula pubescens Ehrh., Pt — Populus tremula, Qr — Quercus robur, Tc — Tilia cordata, Fs — Fagus sylvatica, Ap — Acer platanoides, Ug — Ulmus glabra, Fe — Fraxinus excelsior. aavg, bavg, cavg —параметры уравнения, описывающего среднюю дальность горизонтального распространения корней в зависимости от размеров дерева; amax, bmax, cmax — аналогично для максимальной дальности горизонтального распространения корней (Laitakari, 1927, 1934; Бобкова, 1972; Верхоланцева, Бобкова, 1972; Лащинский, 1981; Диагнозы и ключи …, 1989; Kajimoto et al., 1999; Kalliokoski et al., 2008, 2010a, 2010b; Терехов, Усольцев, 2010; Kalliokoski, 2011); FRff — параметр, описывающий зависимость доли тонких корней, находящихся в подстилке, от мощности подстилки; SRff — аналогично для скелетных корней (Kalela, 1949, 1954; Бобкова, 1972; Верхоланцева, Бобкова, 1972; Банева, 1980; Лозинов, 1980; Лащинский, 1981; Абражко, 1982; Majdi, Persson, 1993; Persson et al., 1995; Braun, Flückiger, 1998; Thomas, Hartmann, 1998; Rust, Savill, 2000; Rothe, Binkley, 2001; Schmid, 2002; Veselkin, 2002; Puhe, 2003; Brandtberg et al., 2004; Leuschner et al., 2004; Oostra et al., 2006; Püttsepp et al., 2006; Withington et al., 2006; Helmisaari et al., 2007, 2009; Ostonen et al., 2007; Tanskanen, Ilvesniemi, 2007; Tatarinov et al., 2008; Dauer et al., 2009; Meinen et al., 2009; Yuan, Chen, 2010; Гиниятуллин, Кулагин, 2012; Peichl et al., 2012; Усольцев, 2013а; Brunner et al., 2013; Chenlemuge et al., 2013; Hansson et al., 2013; Urban et al., 2015; Grygoruk, 2016; Jagodzinski et al., 2016; Takenaka et al., 2016; Tardío et al., 2016; Mauer et al., 2017; Meier et al., 2018; Zhang et al., 2019; Wambsganss et al., 2021); mstrat — множитель, описывающий изменение вертикального распределения биомассы корней в присутствии деревьев других видов (при значениях меньше 1 корневая система становится более глубокой, при значениях больше 1 — более поверхностной) (Büttner, Leuschner, 1994; Schmid, 2002; Schmid, Kazda, 2002; Bolte, Villanueva, 2006; Kelty, 2006; Kalliokoski et al., 2010a, 2010b; Richards et al., 2010; Brassard et al., 2011; Shanin et al., 2015b; Goisser et al., 2016; Jaloviar et al., 2018; Aldea et al., 2021); aur — удельное потребление азота корнями деревьев однолетнего возраста, г азота на кг биомассы тонких корней в сутки; bur — параметр, описывающий снижение удельного потребления азота с возрастом дерева (Gessler et al., 1998; Лебедев, Лебедев, 2011, 2012; Лебедев, 2012а, 2012б, 2013; Guerrero‑Ramírez et al., 2021).
Таблица 3. Видоспецифичные параметры подмодели конкуренции за ФАР (воспроизведено по (Shanin et al., 2020), с изменениями и дополнениями)
| Ps | Pa | Ls | As | Bp | Pt | Qr | Tc | Fs | Ap | Ug | Fe | |
| SHP | EL | CN | CN | CN | SE | SE | CY | SE | SE | EL | SE | EL |
| α | 3.788 | 2.519 | 3.650 | 2.614 | 2.254 | 2.324 | 2.727 | 2.816 | 2.918 | 2.798 | 2.824 | 3.421 |
| ε | 1.283 | 1.448 | 1.262 | 1.422 | 1.386 | 3.392 | 1.656 | 1.700 | 1.316 | 1.702 | 1.714 | 1.186 |
| γ[e−2] | −8.38 | −4.71 | −7.52 | −4.82 | −6.42 | −6.05 | −5.48 | −5.22 | −4.22 | −5.66 | −5.12 | −7.55 |
| μ | 0.724 | 0.926 | 0.712 | 0.888 | 0.682 | 0.715 | 0.694 | 0.702 | 0.816 | 0.688 | 0.710 | 0.615 |
| υCR | 8.882 | 5.757 | 7.955 | 5.402 | 9.147 | 8.412 | 11.178 | 9.120 | 10.912 | 9.064 | 8.842 | 8.764 |
| υCL | 38.167 | 45.420 | 41.714 | 46.166 | 52.571 | 46.271 | 42.718 | 42.172 | 45.212 | 43.224 | 41.716 | 37.162 |
| ηCR[e−2] | −2.04 | −4.82 | −3.02 | −4.22 | −2.54 | −2.61 | −3.04 | −2.71 | −3.12 | −3.14 | −3.22 | −2.81 |
| ηCL[e−2] | −1.37 | −2.43 | −1.64 | −2.49 | −1.42 | −1.55 | −1.49 | −1.88 | −2.52 | −1.96 | −1.78 | −1.32 |
| κCR[e−6] | −4.46 | −1.62 | −3.91 | −1.78 | −4.78 | −4.91 | −3.12 | −2.74 | −1.51 | −2.14 | −1.88 | −4.31 |
| κCL[e−6] | −8.92 | −4.86 | −4.22 | −4.81 | −5.39 | −4.67 | −3.47 | −3.20 | −3.00 | −2.97 | −2.01 | −8.16 |
| σLV | 0.043 | 0.042 | 0.048 | 0.044 | 0.057 | 0.059 | 0.028 | 0.012 | 0.010 | 0.011 | 0.022 | 0.013 |
| σBM | 0.079 | 0.059 | 0.062 | 0.061 | 0.119 | 0.121 | 0.115 | 0.102 | 0.118 | 0.106 | 0.124 | 0.101 |
| τLV | 1.128 | 1.292 | 1.333 | 1.264 | 1.123 | 1.126 | 1.152 | 1.118 | 1.076 | 1.102 | 1.074 | 1.326 |
| τBM | 1.020 | 1.168 | 1.200 | 1.151 | 0.949 | 0.948 | 0.996 | 0.993 | 0.949 | 0.979 | 0.954 | 1.122 |
| ψLV | −3.430 | −2.622 | −2.545 | −2.658 | −3.146 | −3.127 | −3.312 | −3.527 | −3.992 | −3.674 | −3.872 | −2.818 |
| ψBM | −3.596 | −2.589 | −2.428 | −2.602 | −3.907 | −3.878 | −3.622 | −3.722 | −4.061 | −3.840 | −3.912 | −3.022 |
| ωLV | 4.987 | 3.962 | 4.116 | 3.848 | 3.979 | 4.003 | 4.565 | 4.128 | 4.446 | 4.220 | 4.450 | 4.792 |
| ωBM | 3.667 | 2.765 | 2.664 | 2.641 | 3.659 | 3.626 | 4.372 | 4.110 | 4.199 | 4.192 | 4.217 | 4.442 |
| SLV | 8.8 | 5.4 | 4.9 | 9.5 | 18.7 | 17.0 | 17.5 | 22.1 | 21.6 | 23.7 | 24.0 | 16.0 |
| Lmin | 0.340 | 0.015 | 0.320 | 0.010 | 0.290 | 0.180 | 0.105 | 0.010 | 0.008 | 0.010 | 0.010 | 0.050 |
Примечание: Коды видов — аналогично табл. 2. SHP — форма кроны (EL — вертикально-асимметричный эллипсоид, SE — полуэллипсоид, CN — составной конус, CY — цилиндр); α, ε, γ, μ — коэффициенты уравнения для учёта влияния соседних деревьев на размеры кроны фокального дерева; υ, η, κ — коэффициенты уравнения для расчёта размеров кроны (CR — средний радиус в наиболее широкой части, CL — протяжённость в вертикальном направлении) (Пугачевский, 1992; Цельникер и др., 1999; Widlowski et al., 2003; Rautiainen, Stenberg, 2005; Lintunen, Kaitaniemi, 2010; Thorpe et al., 2010; Seidel et al., 2011; Усольцев, 2013б, 2016; Kuehne et al., 2013; Lintunen, 2013; Falster et al., 2015; Pretzsch et al., 2015; Шанин и др., 2016, 2018; Dahlhausen et al., 2016; Danilin, Tselitan, 2016; Barbeito et al., 2017; Pretzsch, 2019; Jucker et al., 2022; Shashkov et al., 2022); σ, τ, ψ, ω — коэффициенты уравнения распределения биомассы листвы (LV) и общей биомассы листвы и ветвей (BM) в вертикальном профиле кроны (Носова, 1970; Гульбе и др., 1983; Niinemets, 1996; Èermák, 1998; Ярмишко, 1999; Бобкова и др., 2000; Mäkelä, Vanninen, 2001; Tahvanainen, Forss, 2008; Petriţan et al., 2009; Lintunen et al., 2011; Hertel et al., 2012; Šrámek, Čermák, 2012; Усольцев, 2013а; Gspaltl et al., 2013; Берлин и др., 2015; Montesano et al., 2015; Hagemeier, Leuschner, 2019a, 2019b; Kükenbrink et al., 2021); SLV — удельная односторонняя площадь листовой поверхности, м2 кг−1 (Росс, 1975; Гульбе и др., 1983; Èermák, 1998; Widlowski et al., 2003; Уткин и др., 2008; Collalti et al., 2014; Thomas et al., 2015; Forrester et al., 2017); Lmin — пороговая величина ФАР, в долях от ФАР над пологом (Evstigneev, 2018; Leuschner, Hagemeier, 2020). Примечания [e−2] и [e−6] после имён параметров означают, что для получения фактического значения параметра приведённую в таблицу величину надо умножить на 10 в соответствующей отрицательной степени.
Таблица 4. Видоспецифичные параметры подмодели продукционного процесса (воспроизведено по (Шанин и др., 2019), с изменениями и дополнениями)
| Ps | Pa | Ls | As | Bp | Pt | Qr | Tc | Fs | Ap | Ug | Fe | |
| T0 | 1 | −3 | −5 | −1 | 2 | 5 | 5 | 5 | 3 | 5 | 5 | 5 |
| T1 | 23 | 17 | 24 | 20 | 18 | 20 | 23 | 25 | 22 | 27 | 25 | 25 |
| T2 | 28 | 27 | 29 | 28 | 30 | 32 | 33 | 35 | 34 | 35 | 34 | 33 |
| D0 | 0.82 | 0.50 | 0.56 | 0.52 | 0.63 | 0.71 | 0.55 | 0.59 | 0.64 | 0.53 | 0.48 | 0.72 |
| D1 | 2.2 | 1.36 | 1.62 | 1.41 | 1.72 | 1.88 | 1.44 | 1.62 | 1.75 | 1.12 | 1.22 | 1.86 |
| ψmin | −3.34 | −0.68 | −1.75 | −1.14 | −1.55 | −1.62 | −1.47 | −1.56 | −1.93 | −1.38 | −1.43 | −2.37 |
| CST | 0.474 | 0.504 | 0.467 | 0.497 | 0.494 | 0.496 | 0.484 | 0.472 | 0.469 | 0.471 | 0.465 | 0.463 |
| CBR | 0.498 | 0.522 | 0.477 | 0.519 | 0.501 | 0.518 | 0.491 | 0.475 | 0.464 | 0.477 | 0.471 | 0.460 |
| CLV | 0.507 | 0.532 | 0.474 | 0.535 | 0.512 | 0.528 | 0.504 | 0.474 | 0.462 | 0.458 | 0.467 | 0.466 |
| CSR | 0.461 | 0.486 | 0.471 | 0.506 | 0.502 | 0.499 | 0.486 | 0.501 | 0.454 | 0.438 | 0.445 | 0.435 |
| CFR | 0.504 | 0.527 | 0.476 | 0.522 | 0.508 | 0.522 | 0.502 | 0.506 | 0.484 | 0.492 | 0.499 | 0.484 |
| NST | 1.4 | 1.6 | 1.7 | 2.2 | 2.1 | 2.7 | 3.1 | 2.8 | 2.4 | 2.7 | 2.8 | 2.8 |
| NBR | 3.2 | 4.2 | 3.8 | 5.4 | 6.4 | 6.3 | 6.9 | 7.2 | 6.2 | 5.6 | 7.2 | 6.8 |
| NLV | 11.9 | 14.1 | 13.3 | 16.4 | 23.7 | 23.9 | 24.8 | 28.9 | 20.3 | 19.6 | 28.1 | 23.6 |
| NSR | 2.2 | 3.8 | 2.9 | 3.9 | 6.0 | 5.4 | 5.7 | 6.7 | 5.2 | 5.6 | 7.1 | 6.5 |
| NFR | 3.7 | 5.7 | 5.1 | 6.8 | 7.5 | 8.0 | 8.7 | 7.9 | 7.5 | 7.8 | 9.6 | 9.1 |
| NLIT | 7.0 | 8.6 | 8.1 | 9.8 | 13.3 | 13.6 | 10.1 | 14.9 | 8.1 | 7.9 | 11.2 | 13.3 |
| A1 | 0.70 | 0.95 | 0.90 | 0.95 | 0.90 | 0.90 | 0.60 | 0.60 | 0.70 | 0.60 | 0.65 | 0.60 |
| A2 | 3.00 | 4.00 | 3.50 | 4.00 | 4.00 | 4.00 | 2.25 | 2.50 | 3.00 | 2.50 | 3.00 | 3.00 |
| Amax | 500 | 600 | 600 | 400 | 250 | 200 | 1200 | 600 | 600 | 450 | 350 | 400 |
| Hmax | 50 | 52 | 48 | 44 | 36 | 38 | 42 | 40 | 48 | 40 | 40 | 52 |
| EVG | + | + | − | + | − | − | − | − | − | − | − | − |
| Pmax | 7.72 | 4.61 | 3.26 | 2.55 | 9.10 | 13.29 | 20.20 | 21.08 | 14.20 | 4.54 | 22.97 | 15.52 |
| Km | 245.78 | 224.41 | 374.19 | 177.56 | 139.02 | 305.56 | 283.00 | 286.72 | 236.60 | 135.25 | 351.25 | 302.24 |
| Kbb | 3.55 | 4.56 | 4.00 | 4.00 | 9.36 | 13.50 | 3.30 | 6.00 | 12.70 | 13.56 | 6.00 | 6.00 |
| ρST | 470 | 405 | 425 | 350 | 590 | 380 | 620 | 470 | 560 | 590 | 595 | 675 |
| z | 1.36 | 0.93 | 0.27 | 0.90 | 0.95 | 0.47 | 0.68 | 0.71 | 0.72 | 0.25 | 1.27 | 0.72 |
| y | 0.12 | 0.45 | 5.54 | 0.75 | 0.42 | 2.23 | 0.93 | 0.93 | 1.24 | 3.37 | 0.18 | 1.11 |
| crank | 0.65 | 0.62 | 0.80 | 0.64 | 0.77 | 0.70 | 0.68 | 0.64 | 0.74 | 0.65 | 0.68 | 0.73 |
| drank | −0.21 | −0.20 | −0.19 | −0.20 | −0.23 | −0.28 | −0.30 | −0.28 | −0.29 | −0.29 | −0.31 | −0.28 |
| erank | −1.72 | −0.76 | −0.55 | −0.78 | −1.35 | −1.57 | −0.78 | −0.68 | −1.35 | −0.78 | −0.81 | −1.17 |
| frank | −0.16 | −0.24 | −0.32 | −0.25 | −0.27 | −0.19 | −0.32 | −0.36 | −0.32 | −0.32 | −0.34 | −0.28 |
| DLIT | 0.36 | 0.23 | 0.22 | 0.37 | 0.39 | 0.39 | 0.42 | 0.39 | 0.39 | 0.41 | 0.36 | 0.39 |
Примечание: Коды видов — аналогично табл. T0 — минимальная температура для продукционного процесса, °C; T1 — температура, соответствующая точке насыщения, выше которой не происходит прироста продуктивности, °C; T2 — температура начала угнетения продукционного процесса, °C (Niinemets et al., 1999; Dreyer et al., 2001; Medlyn et al., 2002; Peng et al., 2002; Mäkelä et al., 2008; Amichev et al., 2010); D0 — значение VPD, до которого его повышение не приводит к снижению устьичной проводимости, кПа; D1 — значение VPD, при котором устьичная проводимость уменьшается вдвое, кПа (Appleby, Davies, 1983; Pigott, 1991; Seidl et al., 2005; Цельникер и др., 2007; Gebauer, 2010; Packham et al., 2012; Kharuk et al., 2017; Thomas et al., 2018); ψmin — пороговое значение влажности почвы, МПа (Jarvis, 1976; Hinckley et al., 1978; Appleby, Davies, 1983; Ranney et al., 1991; Bréda et al., 1995; Hanson et al., 2001; Lemoine et al., 2001; Lexer, Hönninger, 2001; Wullschleger, Hanson, 2003; Шеин, 2005; Seidl et al., 2005; Niinemets, Valladares, 2006; Saxton, Rawls, 2006; Geßler et al., 2007; Dulamsuren et al., 2008; Köcher et al., 2009; Rötzer et al., 2013; Way et al., 2013); CST — содержание углерода в стволе, в долях от абсолютно сухой массы; CBR — аналогичный параметр для ветвей; CLV — аналогичный параметр для листвы/хвои; CSR — аналогичный параметр для скелетных корней; CFR — аналогичный параметр для тонких корней (Peñuelas, Estiarte, 1996; Niinemets, Kull, 1998; Balboa‑Murias et al., 2006; Iivonen et al., 2006; Sinkkonen, 2008; Hansson et al., 2010; Дымов и др., 2012; Peichl et al., 2012; Uri et al., 2012, 2019; Дейнеко, Фаустова, 2015; Медведев и др., 2015; Giertych et al., 2015; Steffens et al., 2015; Zadworny et al., 2015; Zhu et al., 2017; Туменбаева и др., 2018; Koshurnikova et al., 2018; Бетехтина и др., 2019; Каплина, Кулакова, 2021); NST — удельное потребление азота на прирост единицы массы ствола, г азота на 1 кг прироста; NBR — аналогичный параметр для ветвей; NLV — аналогичный параметр для листвы/хвои; NSR — аналогичный параметр для скелетных корней; NFR — аналогичный параметр для тонких корней; NLIT — содержание азота в листовом опаде, г азота на 1 кг опада (Ремезов и др., 1959; Bocock, 1964; Ремезов, Погребняк, 1965; Морозова, 1971, 1991; Новицкая, 1971; Казимиров, Морозова, 1973; Молчанов, Полякова, 1974, 1977; Русанова, 1975; Смеян и др., 1977; Хавроньин и др., 1977; Лукьянец, 1980; Работнов, 1980; Вакуров, Полякова, 1982а, 1982б; Второва, 1982; Оськина, 1982; Бобкова, 1987; Карманова и др., 1987; Столяров и др., 1989; Носова, Холопова, 1990; Мигунова, 1993; Лукина и др., 1994; Bauer et al., 1997; Niinemets, 1998; Trémolières et al., 1999; Судачкова и др., 2003; Peuke, Rennenberg, 2004; Моделирование динамики …, 2007; Nahm et al., 2007; Vesterdal et al., 2008; Dannenmann et al., 2009; Hobbie et al., 2010; Винокурова, Лобанова, 2011; Решетникова, 2011; Дымов и др., 2012; Falster et al., 2015; Матвиенко, 2017); A1, A2 — регрессионные коэффициенты зависимости продукции биомассы от высоты и возраста дерева; Amax — теоретический максимально возможный (для данного вида) возраст, лет; Hmax — теоретическая максимально возможная (для данного вида) высота, м (Prentice, Helmisaari, 1991; Landsberg, Waring, 1997; Lexer, Hönninger, 2001; Усольцев, 2002; Восточноевропейские леса …, 2004; Seidl et al., 2005; Бобкова и др., 2007; Швиденко и др., 2008; Praciak, 2013); EVG — является ли вид вечнозеленым или листопадным; Pmax — максимальная интенсивность фотосинтеза в пересчёте на углерод, μмоль м−2 с−1; Km — интенсивность ФАР, при которой достигается 0.5 от полной интенсивности фотосинтеза, μмоль м−2 с−1 (Kull, Koppel, 1987; von der Heide‑Spravka, Watson, 1992; Kloeppel, Abrams, 1995; Luoma, 1997; Kazda et al., 2000; Oleksyn et al., 2000; Aschan et al., 2001; Zagirova, 2001; Medlyn et al., 2002; Le Goff et al., 2004; Dulamsuren et al., 2009; Gardiner et al., 2009; Ďurkovič et al., 2010; Suvorova et al., 2017; Герлинг, Тарасов, 2020); Kbb —коэффициент Болла-Берри для расчёта устьичной проводимости (Miner et al., 2017; Pace et al., 2021); ρST — плотность стволовой древесины (с учётом коры), кг м−3 (Справочник …, 1989; Zhang et al., 1993; Luostarinen, Verkasalo, 2000; Kärki, 2001; Mäkinen et al., 2002; Alberti et al., 2005; Heräjärvi, Junkkonen, 2006; Lal et al., 2007; Gryc et al., 2008; Jyske et al., 2008; Kiaei, Samariha, 2011; Tomczak et al., 2011; Luostarinen, 2012; Skarvelis, Mantanis, 2013; Mederski et al., 2015; De Jaegere et al., 2016; Diaconu et al., 2016; Díaz‑Maroto, Sylvain, 2016; Hamada et al., 2016; Zajączkowska, Kozakiewicz, 2016; Liepiņš et al., 2017; Viherä‑Aarnio, Velling, 2017; Giagli et al., 2018); z, y — эмпирические коэффициенты для конверсии размеров ствола дерева в его биомассу (Усольцев, 2002, 2016; Швиденко и др., 2008); crank, drank, erank, frank — эмпирические коэффициенты для расчёта распределения массы дерева по органам (Стаканов, 1990; Helmisaari et al., 2002; Falster et al., 2015; Усольцев, 2016; Komarov et al., 2017b); DLIT — параметр, характеризующий дальность разлёта хвойно-листового опада в зависимости от высоты дерева.
Таблица 5. Общие параметры системы моделей (воспроизведено по (Shanin et al., 2015a; Шанин и др., 2019; Shanin et al., 2020), с изменениями и дополнениями)
| Параметр | Значение |
| dT — время задержки реакции на изменение температуры, дней (Mäkelä et al., 2008) | 6 |
| ψfc — водный потенциал почвы при наименьшей полевой влагоёмкости, МПа (Hanson et al., 2001; Wullschleger, Hanson, 2003; Шеин, 2005; Saxton, Rawls, 2006) | −0.033 |
| C0 — базовая концентрация CO2, мл м−3(Friedlingstein et al., 1995; Coops et al., 2005; Seidl et al., 2005; Swenson et al., 2005) | 340 |
| Cb — концентрация CO2 в точке компенсации, мл м−3 (Friedlingstein et al., 1995; Coops et al., 2005; Seidl et al., 2005; Swenson et al., 2005) | 80 |
| β0 — фактор отклика на концентрацию CO2 (Friedlingstein et al., 1995; Norby et al., 2005) | 0.6 |
| w — весовой коэффициент комбинирования факторов среды (Frolov et al., 2020a) | 0.5 |
| CRmax — пороговое отношение максимального радиуса проекции кроны к среднему (Shanin et al., 2020) | 1.25 |
| Kred — коэффициент пропускания ФАР листвой | 0.5 |
| mfert — модификатор дальности горизонтального распространения корневых систем для олиго-, мезо- и эвтрофных местообитаний (Shanin et al., 2015a) | 1.2; 1.0; 0.8 |
| mmoist — модификатор дальности горизонтального распространения корневых систем для местообитаний с низким, умеренным и избыточным увлажнением (Shanin et al., 2015a) | 1.3; 1.0; 0.9 |
| pa — параметр вероятностного самоизреживания древостоев (Seidl et al., 2012) | 0.02 |
| aNmin[L] — параметр функции вычисления минерализации азота в подгоризонтах L органогенного и пулах L органоминерального горизонтов почвы для бореального и умеренного климата | −1.41; −1.26 |
| aNmin[F] — параметр функции вычисления минерализации азота в подгоризонтах F и H органогенного и пуле F органоминерального горизонтов почвы для бореального и умеренного климата | −0.97; −0.88 |
| aNmin[H] — параметр функции вычисления минерализации азота в пуле H органоминерального горизонта почвы для бореального и умеренного климата | −1.37; −1.38 |
| bNmin[L] — параметр функции вычисления минерализации азота в подгоризонтах L органогенного и пулах L органоминерального горизонтов почвы для бореального и умеренного климата | −105.02; −104.92 |
| bNmin[F] — параметр функции вычисления минерализации азота в подгоризонтах F и H органогенного и пуле F органоминерального горизонтов почвы для бореального и умеренного климата | −103.24; −103.87 |
| bNmin[H] — параметр функции вычисления минерализации азота в пуле H органоминерального горизонта почвы для бореального и умеренного климата | −104.43; −104.53 |
Входными переменными системы моделей на этапе инициализации являются: тип местообитания по трофности (олиго-, мезо- или эвтрофное) и по увлажнению (сухое, умеренное (нормальное), переувлажнённое); географические координаты (в десятичных градусах); гранулометрический состав почвы (доли ила, пыли и песка); начальные параметры древостоя (тип пространственного размещения деревьев (псевдослучайное, кластеризованное, регулярная посадка и т. п.), густота (шт га−1), видовой состав, распределение деревьев по высоте и диаметру ствола); параметры микрорельефа (амплитуда высот, тип неоднородностей); толщина всех рассматриваемых слоёв почвы (м); плотность естественного сложения всех рассматриваемых слоёв почвы (кг м−3); плотность твёрдой фазы всех рассматриваемых слоёв почвы (кг м−3); содержание углерода и азота в подгоризонтах L, F и H органогенного горизонта и пулах L, F и H органоминерального горизонта (кг м−2); кислотность почвы, дренированность почвы (логическое значение, высокая/низкая). Входными переменными системы моделей на единичном (суточном) шаге являются: минимальная, средняя и максимальная температура воздуха (°C); дефицит давления водяного пара (кПа); относительная влажность воздуха (%); количество осадков (мм сут−1); концентрация углекислого газа в атмосфере (мл м−3); поступление соединений азота с атмосферными осадками (в пересчёте на азот, кг м−2 сут−1). Предусмотрена имитация рубок (в качестве параметров используются интенсивность рубки, очерёдность изъятия разных видов деревьев при рубке, количество оставляемых порубочных остатков и т. д.) и посадок деревьев (параметры: густота посадки, шт га−1, видовой состав, размеры и параметры пространственного размещения) на определённых шагах моделирования. Система моделей имеет также ряд «технических» параметров (размер имитационной решётки и единичной ячейки имитационной решётки; частота дискретизации кривых, описывающих формы крон, и т. п.), которые здесь не расшифровываются.
Инициализация системы моделей
Микрорельеф
Поскольку микрорельеф является результатом взаимодействия сложного комплекса процессов, протекающих на разных пространственных масштабах и с разными характерными временами, построение процессно-ориентированной модели (т. е. воспроизводящей реальные механизмы формирования микрорельефа) представляется нецелесообразным. Вместо этого алгоритм генерации микрорельефа строится по принципу формирования набора ячеек со статистическими характеристиками распределения относительных высот, заданными в форме внешних параметров подмодели. Для ячейки, имеющей наименьшее значение абсолютной высоты, величина относительной высоты принимается равной 0, а для остальных ячеек высота рассчитывается относительно неё (в метрах). Работа алгоритма включает в себя следующие этапы: (1) генерация «исторической» неоднородности (пространственный масштаб элементов составляет от метров до десятков метров); (2) генерация микронеоднородностей (пространственный масштаб элементов сопоставим с размером ячейки имитационной решётки); (3) генерация неоднородностей, связанных с наличием пристволовых повышений и ветровально-почвенных комплексов (западина, бугор, валёж) (Карпачевский, 1981); (4) генерация общего уклона.
Первый этап предполагает генерацию гауссовского случайного поля (Hristopulos, 2020) с заданными в качестве входных параметров количеством узлов и амплитудой неоднородности (разность между максимальным и минимальным значениями относительных высот ячеек). На втором этапе полученные значения относительных высот модифицируются с помощью равномерно распределённых случайных отклонений, амплитуда которых задаётся входным параметром подмодели. Процедура генерации пристволовых повышений на данном этапе разработки подмодели предусматривает зависимость их величины только от диаметра ствола дерева на уровне груди и принята равной 0.5 от величины последнего. Общий уклон на имитируемом участке рассчитывается с помощью общего уравнения плоскости, параметры которого зависят от заданных в качестве входных параметров азимута (в градусах относительно направления на географический север) и величины уклона (в %).
Пространственная структура древостоя
Структура системы моделей предполагает, что координаты каждого дерева соответствуют координатам центра ячейки, в которой данное дерево размещается, при этом в одной ячейке не может находиться более одного дерева. Подмодель пространственной структуры древостоя позволяет реализовать несколько типов начального размещения деревьев на имитируемом участке.
При реализации равномерного псевдослучайного размещения координаты деревьев псевдослучайным образом выбираются из доступного диапазона. Псевдослучайное размещение c пороговым расстоянием реализовано в двух вариантах. В варианте с приоритетом густоты древостоя на первом этапе алгоритм размещает заданное количество деревьев максимально равномерным образом, для чего используется либо решётка Фибоначчи (Fomin, 1988), либо квадратная сетка с пропуском части элементов. На втором этапе алгоритм случайным образом смещает каждое дерево относительно его исходных координат в пределах определённого расстояния, задаваемого параметром сдвига. Данный параметр определяет максимальное расстояние (в долях единицы) от половины минимального расстояния между деревьями при исходном регулярном размещении. В варианте с приоритетом минимального расстояния алгоритм итеративно пытается разместить каждое новое дерево таким образом, чтобы расстояние от него до ближайшего соседнего составляло не менее чем заданное в параметрах подмодели пороговое расстояние (т. н. «hard-core distance»). Цикл останавливается при превышении порогового числа неудачных попыток найти место для размещения нового дерева (Teichmann et al., 2013). Таким образом, данный алгоритм может не позволить реализовать заданную в начальных параметрах плотность древостоя, но гарантирует соблюдение минимального расстояния между соседними деревьями.
Регулярное размещение деревьев предназначено для имитации посадки лесных культур и имеет два параметра: ширина междурядий и расстояние между саженцами в ряду. При реализации непосредственного размещения деревьев данные параметры дискретизируются с размерностью, равной заданному во входных параметрах подмодели размеру ячейки имитационной решётки.
При реализации кластеризованного размещения алгоритм генерирует гауссовское случайное поле на основе заданного во входных параметрах подмодели количества случайно расположенных узлов. Далее алгоритм реализует распределение заданного количества деревьев в соответствии с вероятностью, описываемой сгенерированным гауссовским случайным полем. Реализация градиентного размещения основана на схожем принципе, но пространственное распределение вероятности описывается уравнением плоскости с заданным во входных параметрах подмодели азимутом. Примеры разных вариантов размещения приведены на рис. 11.
Рисунок 11. Реализация разных вариантов начального размещения деревьев: 1 — равномерное псевдослучайное; 2 — псевдослучайное с пороговым расстоянием (приоритет густоты древостоя); 3 — псевдослучайное с пороговым расстоянием (приоритет минимального расстояния); 4 — кластеризованное; 5 — градиентное; 6 — регулярное
Для имитации неоднородности значений высот и диаметров отдельных деревьев используется β‑распределение (Gupta, 2011). Диапазон значений высоты и диаметра задаётся во входных параметрах подмодели через указание средних, минимальных и максимальных значений данных параметров, что позволяет генерировать асимметричные распределения; также можно указать степень корреляции между значениями высоты и диаметра для отдельных деревьев. Дополнительный параметр позволяет указать форму распределения (выпуклое, вогнутое, равномерное). Структура подмодели позволяет имитировать многовидовые древостои, при этом можно задавать соотношение между видами при определённом типе пространственной структуры или комбинировать древостои из нескольких видов, каждый из которых характеризуется своими особенностями пространственной структуры.
Единичный шаг системы моделей
Конкуренция за минеральный азот в почве
Подмодель конкуренции между деревьями за минеральный азот в почве, подробно описанная ранее (Shanin et al., 2015a), имитирует рост и развитие корневых систем с учётом их адаптации к пространственной неоднородности в распределении почвенных ресурсов и конкурентного давления со стороны соседей. Предполагается, что в пределах каждой ячейки имитируемой площадки распределение ресурсов и биомассы корней однородно. Подмодель является индивидуально-ориентированной и пространственно-детализированной, т. е. учитывает относительное положение и характеристики всех конкурирующих деревьев в древостое, а зона питания каждого дерева представлена в виде массива ячеек.
Общая площадь зоны питания каждого дерева рассчитывается на основе средней (lavg) и максимальной (lmax) дальности распространения корней (м):
где DBH — диаметр ствола дерева на высоте груди (см), aavg, amax, bavg, bmax, cavg и cmax — эмпирические коэффициенты. Поскольку дальность распространения корней снижается с увеличением плодородия и влажности почвы, данные параметры модифицируются в зависимости от условий местообитания: влажности и трофности (дополнительные множители mfert и mmoist). Площадь, занимаемая корневой системой, рассчитывается на основе средней дальности распространения корней как площадь круга с радиусом, равным lavg.
Для определения условий включения ячейки (x,y) в зону питания дерева используется параметр px,y, который зависит от количества азота в доступных для растений формах (кг м−2, является выходной переменной подмодели динамики органического вещества почвы) в данной ячейке (nx,y), расстояния между центром данной ячейки и основанием ствола фокального дерева (dx,y) и массы корней других конкурирующих деревьев (кг м−2, является выходной переменной подмодели продукции и распределения биомассы по органам) в данной ячейке (mx,y):
![]() где значения соответствующих переменных нормируются для приведения их к диапазону [0; 1]. Поскольку зависимость предпочтительности включения ячейки в зону питания дерева от расстояния до ствола фокального дерева и от биомассы корней конкурирующих деревьев снижается по мере роста показателя, дополнительно производится инверсия нормированных значений (1 − f(x)):
где значения соответствующих переменных нормируются для приведения их к диапазону [0; 1]. Поскольку зависимость предпочтительности включения ячейки в зону питания дерева от расстояния до ствола фокального дерева и от биомассы корней конкурирующих деревьев снижается по мере роста показателя, дополнительно производится инверсия нормированных значений (1 − f(x)):
Параметр px,y рассчитывается отдельно для каждого дерева. Расчёт производится для всех ячеек, которые находятся внутри потенциальной зоны корневого питания (круг с радиусом lmax), но ещё не включены в фактическую зону. Далее ячейки включаются в зону питания в соответствии со значением параметра px,y.
Биомасса тонких корней дерева распределяется по ячейкам зоны питания пропорционально сумме значений в данной ячейке f(mx,y) и f(nx,y), биомасса скелетных корней — пропорционально значениям f(dx,y). Вертикальное распределение биомассы корней каждого дерева между подстилкой и минеральной почвой описывается следующим образом:
 где mff — доля общей биомассы корней (отдельно для тонких и скелетных) в данной ячейке, находящаяся в лесной подстилке; ff — толщина лесной подстилки (см), aff — видоспецифичный коэффициент (также различается для скелетных (SRff) и тонких (FRff) корней).
где mff — доля общей биомассы корней (отдельно для тонких и скелетных) в данной ячейке, находящаяся в лесной подстилке; ff — толщина лесной подстилки (см), aff — видоспецифичный коэффициент (также различается для скелетных (SRff) и тонких (FRff) корней).
Коэффициент aff имеет видоспецифичный модификатор mstrat, позволяющий учесть эффект изменения в вертикальной стратификации биомассы корней деревьев разных видов при их совместном произрастании (Brassard et al., 2011; Shanin et al., 2015b). Параметры вертикального распределения биомассы корней рассчитываются отдельно для каждой из ячеек. Схема работы алгоритма представлена на рис. 12.
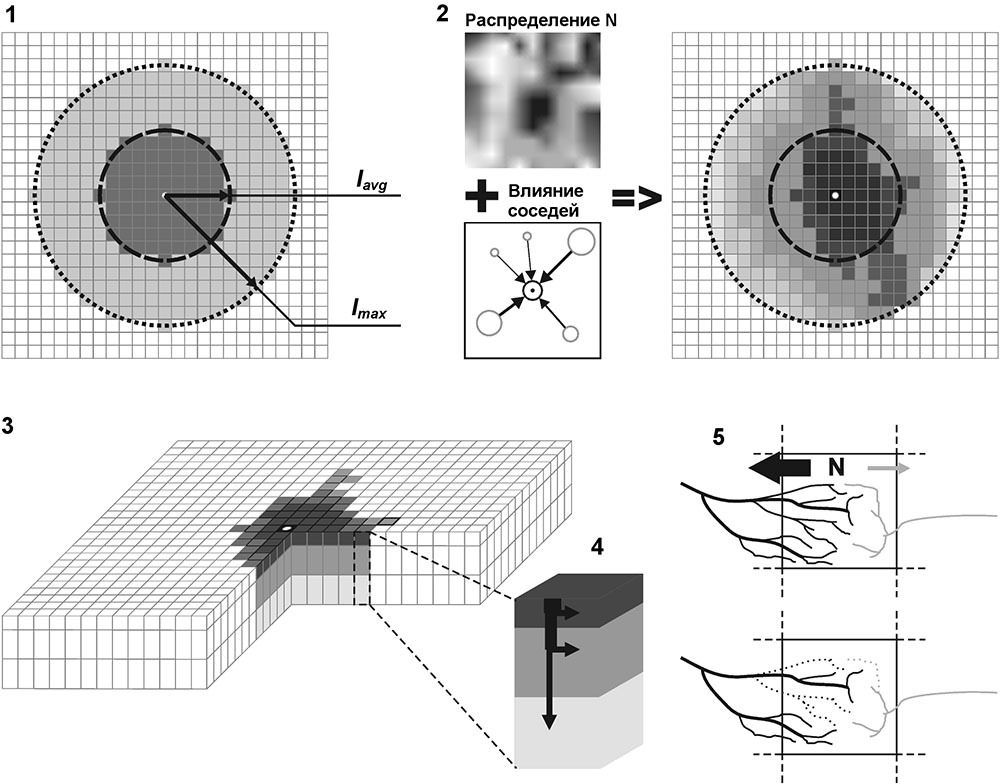
Рисунок 12. Блок-схема алгоритма годичного шага подмодели конкуренции за доступный азот почвы: 1 — расчёт площади зоны корневого питания на основе lavg (тёмно-серая область) и определение всех ячеек, которые потенциально могут быть включены в зону питания, на основе lmax (светло-серый); 2 — расчёт параметра предпочтительности для каждой ячейки в потенциальной зоне питания с учётом неоднородности распределения ресурса и конкурентного давления со стороны соседних деревьев; 3 — включение ячеек в зону корневого питания, при этом биомасса тонких корней распределяется между ячейками в соответствии со значениями px,y; 4 — расчёт вертикального распределения биомассы корней в каждой ячейке; 5 — расчёт поглощения азота в доступных для растений формах в соответствии с биомассой тонких корней каждого конкурирующего дерева. Воспроизведено по (Shanin et al., 2015a)
Поглощение питательных веществ моделируется независимо для каждой ячейки. Предполагается, что доступный азот распределяется между конкурирующими деревьями пропорционально соотношению биомасс их тонких корней в данной ячейке (Pagès et al., 2000; Schiffers et al., 2011), с дополнительным модификатором, зависящим от возраста (Лебедев, 2012а; Лебедев, Лебедев, 2012):
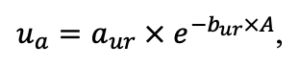
где A — возраст дерева (лет), aur, bur — видоспецифичные эмпирические коэффициенты. Согласно принятым допущениям, весь доступный для деревьев азот полностью поглощается из ячейки за единичный шаг по времени.
Конкуренция за фотосинтетически активную радиацию
Подмодель конкуренции между деревьями за ФАР, подробно описанная ранее (Shanin et al., 2020), как и подмодель конкуренции за ресурсы почвы, является индивидуально-ориентированной и пространственно-детализированной, т. е. учитывает относительное положение и характеристики всех конкурирующих деревьев в древостое. Имитируемый участок разбивается на трёхмерные ячейки, представленные в виде прямоугольных призм с размером основания, равным размеру ячейки имитационной решётки. Высота ячеек также задаётся в настройках подмодели. Кроны всех деревьев аппроксимируются такими ячейками, каждая ячейка может содержать крону только одного дерева. Подмодель требует следующих входных данных: пространственное расположение, вид, возраст, высота и диаметр ствола на высоте груди для каждого отдельного дерева. Выходными данными подмодели являются количество ФАР, поглощённое каждым деревом, и пространственное распределение интенсивности ФАР под пологом. Подмодель является динамической и способна воспроизводить изменения формы кроны отдельных деревьев с течением времени в результате конкуренции.
Размер кроны определяется (а) общей высотой дерева, (б) высотой точки прикрепления кроны и (в) максимальной шириной кроны. Крона представлена одним из осесимметричных тел: цилиндром, вертикально-асимметричным эллипсоидом, полуэллипсоидом, цилиндром, составным конусом и перевёрнутым конусом. Формы крон основаны на базовых формах, представленных в некоторых предыдущих работах (например, Pretzsch et al., 2002; Widlowski et al., 2003), с дополнительными модификациями (рис. 13).
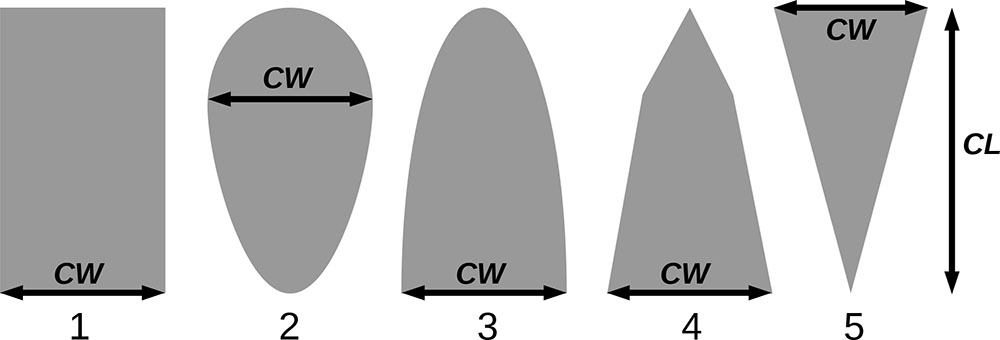
Рисунок 13. Плоские фигуры, формирующие осесимметричные тела для представления видоспецифичных форм крон: 1 — цилиндр, 2 — вертикально-асимметричный эллипсоид, 3 — полуэллипсоид, 4 — составной конус, 5 — перевёрнутый конус. CW обозначает ширину кроны в самой широкой её части (т. е. удвоенный максимальный радиус кроны), CL обозначает протяжённость кроны в вертикальном направлении (общая высота дерева за вычетом высоты прикрепления кроны). Воспроизведено по (Shanin et al., 2020)
Уравнение для расчёта потенциального радиуса кроны использует в качестве предикторов диаметр ствола на высоте груди (DBH). Уравнение для расчёта фактической протяжённости кроны в вертикальном направлении использует в качестве предикторов высоту дерева (H) и локальные индексы конкуренции (Thorpe et al., 2010):
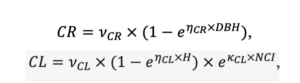
где CR — радиус кроны в наиболее широкой части, CL — протяжённость кроны в вертикальном направлении, NCI — индекс конкуренции, представляющий локальную плотность древостоя вокруг данного дерева (см. ниже), ν, η и κ — эмпирические коэффициенты (индекс CR соответствует коэффициентам для радиуса кроны, а индекс CL — для протяжённости кроны). Таким образом, интенсивность конкуренции (выраженная через локальную плотность древостоя вокруг фокального дерева) влияет на размер кроны. Протяжённость кроны рассматривается как общая высота дерева за вычетом высоты точки прикрепления кроны.
При расчете индексов конкуренции учитывалось влияние всех деревьев (j = 1 … n) разных видов (i = 1 … s), расположенных не далее 10 м от фокального дерева. Подмодель учитывает снижение конкурентного давления со стороны соседей с увеличением размера фокального дерева:
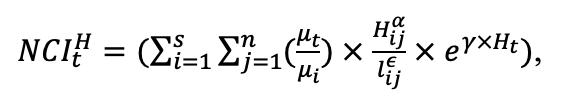
где lij — расстояние между фокальным и конкурирующим деревом, Hij — общая высота конкурирующего дерева, Ht — общая высота фокального дерева t; α, ε, γ, μ — видоспецифичные эмпирические коэффициенты (Thorpe et al., 2010).
Полученные трёхмерные объекты, описывающие форму и размеры крон отдельных деревьев, разбиваются на горизонтальные слои с интервалом 1 м. Если крона не занимает весь слой по вертикали (что возможно для нижнего и верхнего из слоёв, на которые приходится крона), то при аппроксимации подмодель принимает, что крона представлена в данном слое, если она занимает более половины высоты слоя. Чтобы избежать случаев, когда крона не представлена ни в одном слое, для деревьев, кроны которых занимают менее половины любого слоя в вертикальном направлении, подмодель принимает, что крона представлена в слое, в котором её расширение в вертикальном направлении максимально. Радиус кроны в каждом слое рассчитывается как радиус осесимметричного тела, представляющего основную форму кроны на относительной высоте, соответствующей средней точке данного слоя. Внутри слоя крона аппроксимируется прямоугольными призмами.
Для модификации радиуса кроны вследствие конкурентного давления со стороны соседних деревьев, для каждого дерева необходимо определить области, которые потенциально могут быть заняты его кроной. Этот этап предполагает разбиение имитируемого участка на подмножества ячеек, где каждое подмножество соответствует двум условиям: (а) находится ближе к данному дереву, чем к другим деревьям, что осуществляется посредством реализации разбиения Вороного (Tran et al., 2009) в дискретном пространстве и (б) количество ячеек, занятых кроной дерева в данном слое, не превышает потенциальной площади проекции кроны (численно равна площади круга с радиусом, равным радиусу кроны в данном слое). Такие подмножества строятся отдельно для каждого слоя, и при разбиении учитываются только те деревья, кроны которых представлены в данном слое.
На следующем этапе подмодель имитирует распределение биомассы фотосинтезирующих (листья или хвоя) и нефотосинтезирующих (ствол и ветви) органов между ячейками, составляющими крону дерева. Биомассы различных органов дерева являются выходными параметрами подмоделей продукции и распределения биомассы (Шанин и др., 2019). Подмодель учитывает неоднородность как вертикального, так и горизонтального (от ствола до периферии кроны и в разных направлениях) распределения биомассы между ячейками, тогда как распределение биомассы внутри ячейки полагается однородным. Подмодель основана на допущении, что пространственная асимметрия в распределении фотосинтезирующих органов внутри кроны определяется преимущественно конкуренцией со стороны соседних деревьев. Вертикальное распределение биомассы внутри кроны описывается следующим образом:
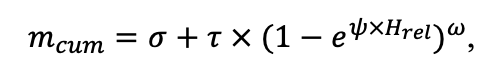
где mcum — накопленная относительная масса компонента кроны (фотосинтезирующих или нефотосинтезирующих органов) в данной ячейке, Hrel — относительная высота данной точки внутри кроны (принимая общую длину кроны за 1), σ, τ, ψ, ω — эмпирические коэффициенты (Tahvanainen, Forss, 2008). Далее применяется масштабирование для установки mcum равным 1 при Hrel равном 1. Вертикальное распределение биомассы ствола рассчитывается на основе его представления в виде усечённого конуса, строго круглого в любом горизонтальном сечении, с радиусом верхней окружности, равным 0.25 от радиуса основания. Биомасса ствола в каждом слое добавляется к биомассе ветвей для ячейки, горизонтальные координаты которой совпадают с координатами основания ствола. Согласно алгоритму, сначала производится распределение биомассы по горизонтальным слоям кроны каждого дерева и далее рассчитывается распределение биомассы между ячейками внутри данного слоя.
Поскольку подробные данные о радиальном распределении фитомассы отсутствуют, описание радиального распределения биомассы внутри кроны основано на предположении, что биомасса фотосинтезирующих органов линейно увеличивается от центра кроны к периферии и от северной к южной части отдельной кроны (Olchev et al., 2009; Bayer et al., 2018). Построение фактической формы кроны схематично представлено на рисунке 14.
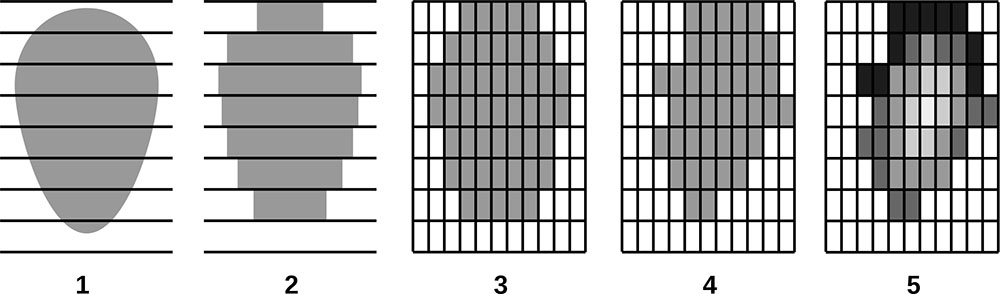
Рисунок 14. Схематическое изображение алгоритма построения фактической формы кроны (в качестве примера взято вертикальное сечение кроны, не проходящее через ствол): 1 — базовая форма кроны; 2 — разделение кроны на горизонтальные слои; 3 — аппроксимация кроны трёхмерными ячейками; 4 — модификация формы кроны в горизонтальном направлении в соответствии с асимметричным конкурентным давлением со стороны соседних деревьев; 5 — распределение надземной биомассы между ячейками. Воспроизведено по (Shanin et al., 2020)
Поступление и поглощение фотосинтетически активной радиации (ФАР) в каждой ячейке (x,y,z) вычисляется как сумма величин прямой и рассеянной ФАР, в свою очередь рассчитываемых как произведения значений их суточных сумм над пологом в данный день на соответствующие значения относительных величин (коэффициентов) пропускания и/или поглощения для каждой ячейки:
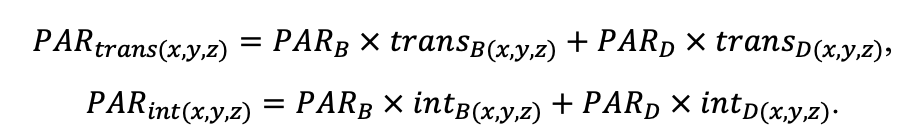
Приходящая солнечная радиация над пологом рассчитывается исходя из траектории видимого движения Солнца по небосводу, а также от облачности, в данной версии подмодели косвенно учитываемой через суточный диапазон температуры воздуха. Необходимые астрономические вычисления выполняются согласно (Strous, 2022).
Высота hʘ и азимут ψʘ Солнца рассчитываются на основе зависимостей:
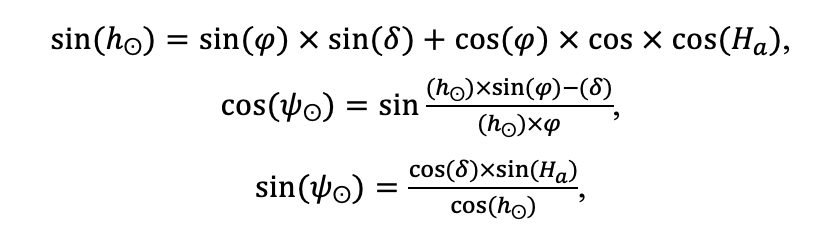
а продолжительность светового дня рассчитывается как
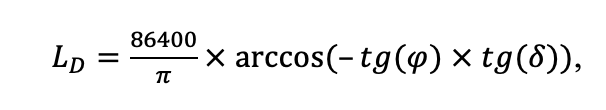
где φ — широта, Ha — часовой угол (время относительно истинного полудня, выраженное в радианах), δ — склонение Солнца (зависящее от порядкового номера дня в году d):
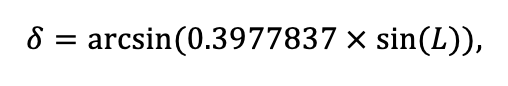
где L — эклиптическая долгота:
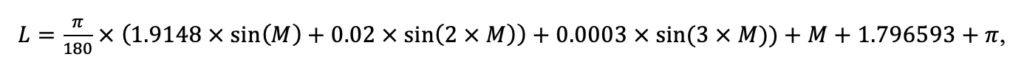
M — средняя аномалия орбиты:
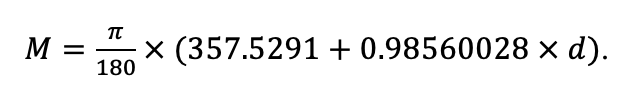
Внеатмосферная интегральная солнечная радиация, приходящая на перпендикулярную лучам поверхность, вычисляется по уравнению:
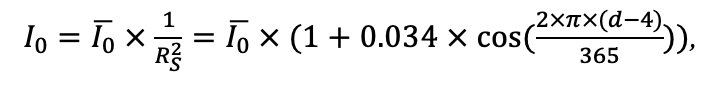
где ![]() =1367 Вт м−2 — солнечная постоянная, — расстояние от Земли до Солнца (а. е.), d — порядковый номер дня в году. Внеатмосферная инсоляция на горизонтальную поверхность, соответственно, рассчитывается как
=1367 Вт м−2 — солнечная постоянная, — расстояние от Земли до Солнца (а. е.), d — порядковый номер дня в году. Внеатмосферная инсоляция на горизонтальную поверхность, соответственно, рассчитывается как
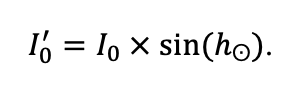
Соответствующая дневная сумма рассчитывается как
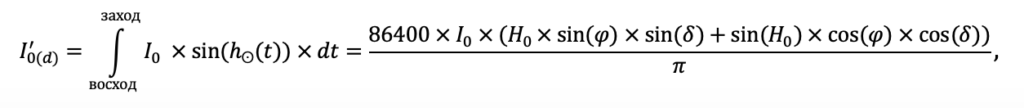
где Н0 — часовой угол захода Солнца.
Внеатмосферные потоки ФАР рассчитываются аналогичным образом, используя вместо интегральной солнечной постоянной соответствующее значение для ФАР:
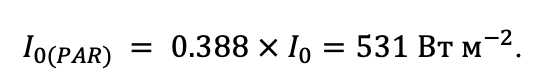
Расчёт суммарной интегральной солнечной радиации при фактических условиях облачности производится по внеатмосферной инсоляции и суточному диапазону изменения температуры воздуха (ΔT = Tmax — Tmin), используемому в качестве косвенной характеристики условий облачности (Bristow, Campbell, 1984):
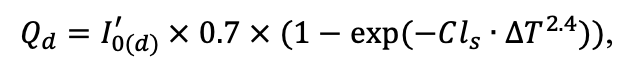
где коэффициент Cls = 0.004 для тёплого времени года и 0.010 — для холодного.
Далее для оценки потоков ФАР рассчитываются суточные суммы суммарной ФАР по сумме интегральной суммарной радиации и её отношению к значению внеатмосферной инсоляции с использованием зависимости, основанной на данных (Yu et al., 2015):
Для разделения суммарной ФАР на прямую S’PAR и рассеянную DPAR используется зависимость относительной доли рассеянной ФАР в суммарной (kdp) от отношения фактической суммарной ФАР к соответствующему внеатмосферному значению (ktp = QPAR(d) / I’PAR(d)), аппроксимированная нами на основании данных Jakovides et al. (2010):
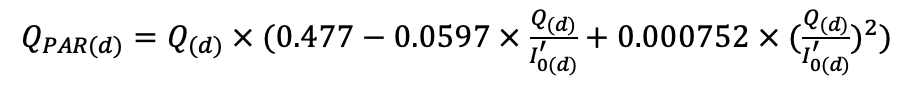
Отсюда:
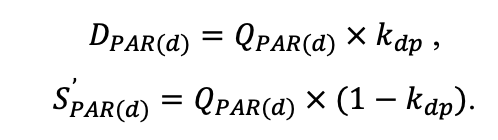
В предположении о независимом от направления (изотропном) поступлении рассеянной радиации над пологом, сферическая облучённость рассеянной радиацией равна её удвоенному потоку на горизонтальную поверхность (van der Hage, 1993):
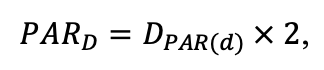
а сферическая облучённость прямой ФАР равна её потоку на перпендикулярную поверхность и оценивается из соотношения
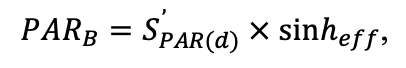
где sinheff = S’d / Sd — отношение суточных сумм прямой радиации на горизонтальную и на перпендикулярную солнечным лучам поверхности (средневзвешенный за день, или «эффективный», синус высоты Солнца), связь которого с высотой Солнца в полдень hʘmax оценена нами по данным Научно-прикладного справочника по климату СССР (1988–2002) для 32 станций лесной зоны ЕТР:
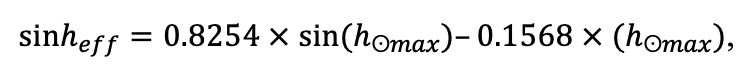
где
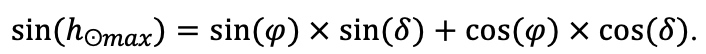
Относительные величины (коэффициенты) пропускания и поглощения ФАР, осреднённые по направлениям поступающей радиации, рассчитываются для каждой ячейки. Для рассеянной радиации — дважды в год (для вегетационного периода и для холодного времени года, c учётом наличия/отсутствия листвы листопадных пород), для прямой — с учётом траектории видимого движения Солнца по небосводу для середины каждого месяца.
Направления расчётных лучей рассеянной радиации рассчитываются по алгоритму решётки Фибоначчи (Stanley, 1988) с целью их равномерного распределения по небесной полусфере. При принятом допущении об изотропности, доля энергии рассеянной радиации, приходящаяся на каждое из n расчётных направлений, равна 1 / n.
Направления лучей прямой радиации для расчёта относительных значений пропускания (поглощения) задаются с интервалом 1 час. Распределение энергии по направлениям задаётся пропорционально доле соответствующих часовых сумм в суточной сумме прямой ФАР на перпендикулярную лучам поверхность.
Для этого рассчитывается прямая интегральная радиация на перпендикулярную поверхность при ясном небе в зависимости от высоты Солнца и коэффициента прозрачности атмосферы P2 (Евневич, Савиковский, 1989):
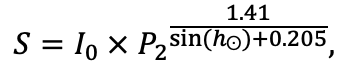
а затем с учётом относительной доли ФАР в интегральной прямой радиации (Mõttus et al., 2001):
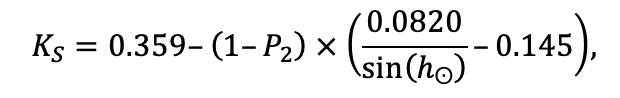
рассчитывается прямая ФАР:
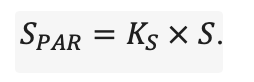
Соответствующая суточная сумма рассчитывается как
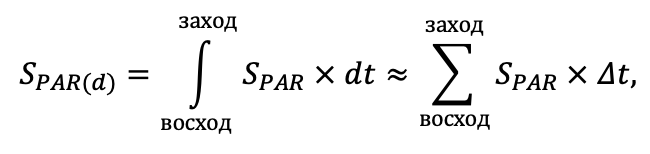
где Δt = 3600 с. А доли в ней, приходящиеся на каждое i‑ое из расчётных направлений, соответственно:
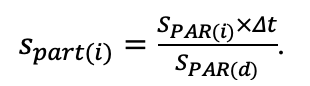
Расчёт относительного пропускания радиации для каждого направления i в каждом слое z рассчитывается исходя из длины пути i‑го луча в слое Δli = 1 / sin(hi) и коэффициентов поглощения k(x,y,z) радиации во входной и выходной ячейках, пересекаемых лучом в данном слое. Коэффициенты поглощения рассчитываются по сумме относительной площади листьев (LAD — Leaf Area Density) и нефотосинтезирующих фитоэлементов (WAD — Wood Area Density), представленных в данной ячейке. В простейшем случае (в соответствии с предположением о случайном размещении фитоэлементов внутри ячейки и их равномерной ориентации по направлениям):
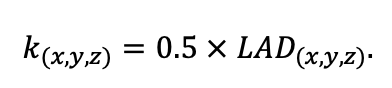
Ослабление i‑го луча в слое z вычисляется как экспонента произведения коэффициентов ослабления на длину луча в слое, а общее ослабление луча, достигшего ячейки (x,y,z), aT(i,x,y,z), равно произведению коэффициентов пропускания всех пройденных лучом слоёв.
Коэффициент пропускания для соответствующей составляющей сферической облученности рассчитывается как средневзвешенная величина по всем направлениям с учётом их доли в суточных суммах ФАР, поступающих на верхнюю границу полога. Таким образом:
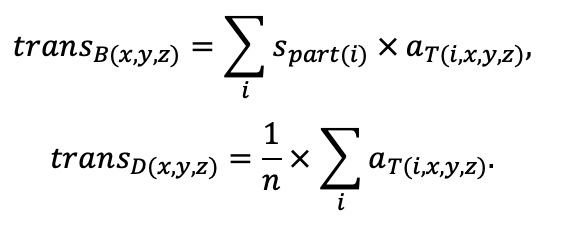
Относительное поглощение листвой в ячейке, соответственно, рассчитывается по дошедшей до ячейки радиации и k(LAD) в ячейке. Если k(x,y,z) не зависит от направления (равномерная ориентация листьев), поглощение ФАР листвой в ячейке пропорционально сферической облучённости:
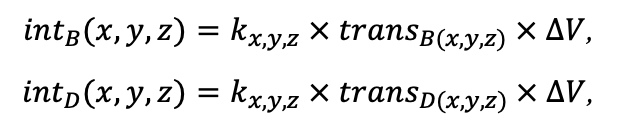
где ΔV — объём ячейки.
Поступление радиации на поверхность почвы (напочвенного покрова) рассчитывается в терминах плотности потока на горизонтальную (или наклонную в случае учёта микрорельефа) поверхность с учётом наклона лучей и их ослабления. В частности, для горизонтальной поверхности все значения пропускания отдельных лучей перед суммированием домножаются на соответствующее значение sin(hi).
Сумма поглощённой ФАР в квантовом выражении (uAPAR) рассчитывается с учетом квантового эквивалента ФАР, принимаемого равным 4.56 моль МДж−1 (Mõttus et al., 2013).
Продукция биомассы деревьев
Подмодель продуктивности, подробно описанная ранее (Шанин и др., 2019), основана на алгоритмах известной модели 3‑PG (Landsberg, Waring, 1997; Seidl et al., 2012), которая обеспечивает упрощённое воспроизведение основных экофизиологических процессов и позволяет рассчитать продукцию биомассы отдельного дерева в зависимости от количества полученных им ресурсов и от реакции дерева на изменение внешних условий.
Потенциальная валовая первичная продукция (вычисляемая в килограммах абсолютно сухой массы, приходящейся на одно дерево) на основе перехваченной деревом ФАР рассчитывается с суточным шагом как
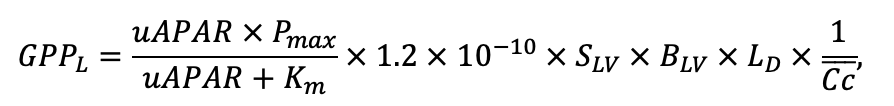
где uAPAR — поглощённая деревом ФАР (μмоль м−2 с−1, вычисляется в подмодели кроновой конкуренции); Pmax — видоспецифичная максимальная интенсивность фотосинтеза в пересчёте на углерод, μмоль м−2 с−1; Km — интенсивность ФАР, при которой достигается 0.5 от полной интенсивности фотосинтеза, μмоль м−2 с−1; 1.2 × 10−10 — коэффициент пересчёта из μмоль в кг углерода; SLV — удельная односторонняя площадь листовой поверхности, м2 кг−1; BLV — общая биомасса листвы дерева, кг (используется для перехода от 1 м2 листовой поверхности к общей листовой поверхности дерева); LD — продолжительность светового дня, сек, ![]() — средневзвешенная концентрация углерода по всем фракциям биомассы дерева.
— средневзвешенная концентрация углерода по всем фракциям биомассы дерева.
Модификатор, зависящий от температуры воздуха (Mäkelä et al., 2004), рассчитывается с суточным шагом (d) на основе модели задержки первого порядка. На первом этапе вычисляется TE — «сглаженная» температура, учитывающая инерцию температурной акклиматизации и рассчитываемая на основе средней дневной температуры воздуха за текущие (d) и предшествующие (d−1) сутки:
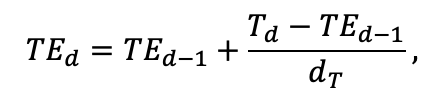
где dT — биом-специфичная константа, определяющая время задержки (в днях) реакции на изменение температуры (Mäkelä et al., 2008), Td — средняя дневная температура воздуха.
Состояние температурной акклиматизации TA выводится на основе порогового значения (биологического минимума фотосинтеза) температуры T0:
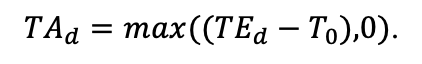
Итоговое значение зависящего от температуры модификатора fT рассчитывается относительно температуры уровня насыщения T1. Кроме того, в процедуру расчёта модификатора был введён параметр T2, позволяющий учитывать снижение продуктивности при росте температуры выше порогового уровня:
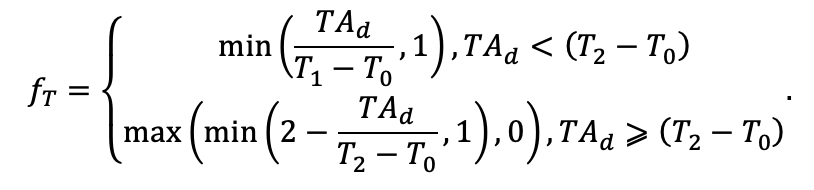
Таким образом, T0 — температура, при которой продукционный процесс останавливается, T1 — температура, соответствующая точке насыщения, выше которой не происходит прироста продуктивности, а T2 — температура, при которой начинается угнетение продукционных процессов вследствие теплового стресса.
Отклик продуктивности, связанный с дефицитом насыщения водяного пара VPD, основан на аналогичной по назначению функции, применяемой в эколого-физиологической модели М. Д. Корзухина и Ю. Л. Цельникер (Корзухин и др., 2004, 2008; Цельникер и др., 2007, 2010; Корзухин, Цельникер, 2009, 2010). Данный модификатор вычисляется следующим образом:
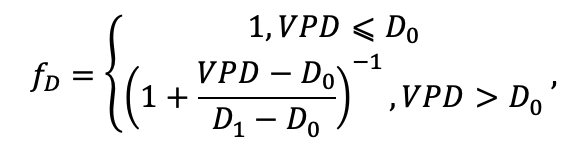
где VPD — дефицит насыщения водяного пара (кПа); D0, D1 — эмпирические параметры (D0 соответствует значению VPD, до которого его повышение не приводит к снижению проводимости, а D1 — значению VPD, при котором устьичная проводимость уменьшается вдвое).
Модификатор отклика продуктивности в зависимости от доступности влаги в почве вычисляется на основе потенциала почвенной влаги ψ (Hanson et al., 2001; Wullschleger, Hanson, 2003). Он является линейной функцией от ψ в пределах от наименьшей полевой влагоёмкости ψfc до видоспецифичного ψmin:
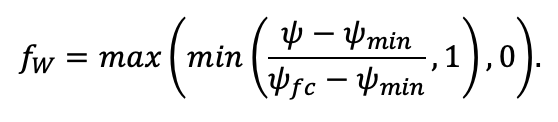
Зависимость эффективности использования ФАР от концентрации CO2 рассчитывается как
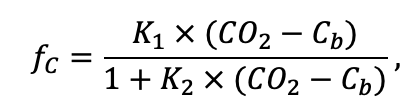
где
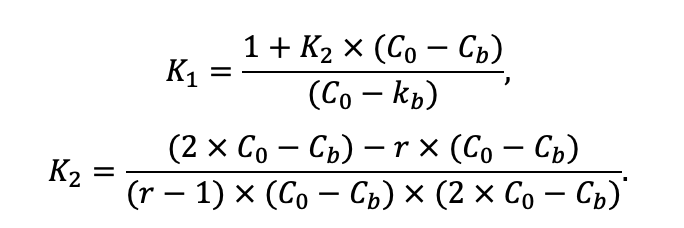
Здесь CO2 и C0 — текущая и базовая концентрации CO2 соответственно. Cb соответствует точке компенсации фотосинтеза и равна 80 ppm (Coops et al., 2005).
Перехват ФАР для листопадных видов ограничен продолжительностью вегетационного периода, которая определяется значением вегетативного индекса GSI. Для его расчёта использовались такие параметры, как продолжительность фотопериода L, минимальная суточная температура Tmin и дефицит насыщения водяного пара VPD.
Эффект снижения продуктивности в ходе старения дерева (fA) рассчитывается следующим образом (Räim et al., 2012):
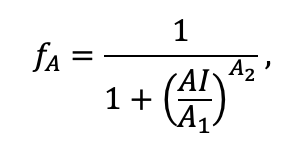
где A1 и A2 — эмпирические коэффициенты, а AI рассчитывается как
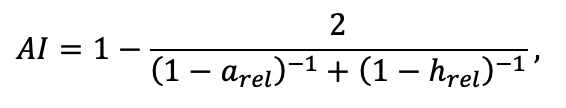
где относительный возраст arel и относительная высота hrel рассчитываются как отношение возраста и высоты дерева к соответствующим видоспецифичным максимумам (Amax, Hmax) и являются показателями старения.
Зависимость продуктивности от количества потреблённого деревом азота (fN) рассчитывается на основе величины максимального теоретического потребления азота деревом (на 1 кг прироста):
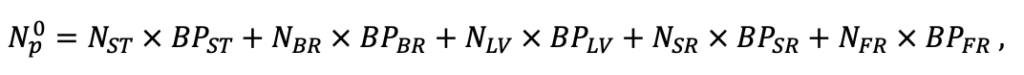
где Ni — удельное потребление азота разными органами дерева, в кг азота на 1 кг прироста биомассы органа, BPi — доля прироста данного органа в общем приросте биомассы (см. ниже), где i соответствует индексам разных органов дерева (ST — ствол, BR — ветви, LV — листва или хвоя, SR — скелетные корни, FR — тонкие корни).
Потенциальная продуктивность в зависимости от количества доступного азота рассчитывается исходя из количества (кг) азота, потреблённого деревом из почвы (Nuptake), которое рассчитывается в подмодели корневой конкуренции; также учитывается количество запасённого деревом буферного азота (Nbuffer):
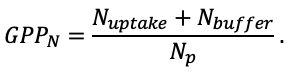
Значение модификатора fN рассчитывается исходя из отношения потенциального прироста в зависимости от количества доступного азота и потенциального прироста, лимитированного прочими факторами. Значение модификатора ограничено сверху значением 1, характеризуя таким образом выход функции на насыщение:
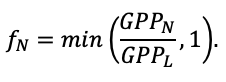
Эффективность использования ресурсов γeff (Seidl et al., 2005; Swenson et al., 2005) зависит от модификаторов, связанных с условиями окружающей среды и физиологическими особенностями дерева:
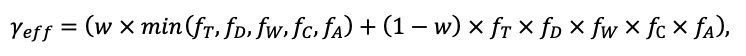
где эмпирически подобранное значение коэффициента w (Frolov et al., 2020a) определяет баланс между двумя методами оценки взаимодействия между модификаторами.
Фактическая валовая первичная продукция рассчитывается как
![]()
Избыточный поглощённый азот сохраняется в форме буферного запаса. Также подмодель учитывает перемещение части азота из отмирающей листвы/хвои (LITLV) в азотный буфер перед её опаданием:
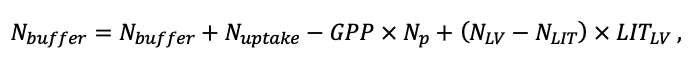
где NLIT — содержание азота в опаде листвы/хвои, LITLV — масса годичного опада листвы/хвои.
Дыхание в пересчёте на углерод (C‑CO2) рассчитывается с суточным шагом и состоит из двух компонентов. Дыхание поддержания вычисляется как
![]()
где BLV, BFR, BST, BBR, BSR — биомасса листвы/хвои, тонких корней, ствола, ветвей и скелетных корней соответственно, CLV, CFR, CST, CBR, CSR — содержание углерода в листве/хвое, тонких корнях, стволе, ветвях и скелетных корнях в долях от абсолютно сухой массы, а Q10 вычисляется как
![]()
где Td — средняя дневная температура воздуха (Wang et al., 2011).
Второй компонент (дыхание роста) вычисляется как постоянная доля от валовой первичной продукции (Jiao et al., 2022):
![]()
Чистая первичная продукция равна валовой первичной продукции за вычетом затрат на дыхание:
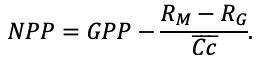
Если значение fN меньше 1, избыток ассимилятов конвертируется в количество корневых экссудатов:
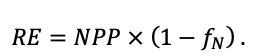
Расчёт устьичной проводимости листьев деревьев производится с учётом интенсивности фотосинтеза, относительной влажности воздуха (rh) и концентрации CO2 на поверхности листа (Cs) по формуле (Pace et al., 2021):
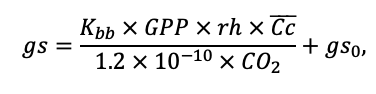
где Kbb — коэффициент Болла-Берри (безразмерный), GPP — валовая первичная продукция (в пересчёте на углерод, μмоль м−2 с−1), CO2 — объёмная концентрация CO2 (μмоль моль−1), gs0 — минимальное значение устьичной проводимости (моль м−2 с−1).
Согласно (Zhu et al., 2011), транспирация деревьев (ET, кг м−2 с−1) рассчитывается как
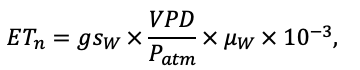
где gsW — устьичная проводимость H2O, равная (gs / 1.6), VPD — дефицит давления водяного пара между межклеточным пространством и воздушным слоем непосредственно над поверхностью листа (принимаемый равным VPD атмосферного воздуха в предположении о насыщающей влажности воздуха в межклеточном пространстве и равенства температур листа и окружающего воздуха), Patm — атмосферное давление, принимаемое постоянным и равным 105 Па, μW — молярная масса воды (г моль−1).
Аллокация биомассы и пространственное распределение опада
Для описания распределения прироста биомассы между органами дерева используется уравнение рангового распределения, более подробно описанное в предшествующих работах (Komarov et al., 2017b; Шанин и др., 2019). Применительно к биомассе деревьев, ранг характеризует место соответствующего органа дерева в ряду, упорядоченном по убыванию количества поступившего ресурса. Соответственно, данное распределение позволяет рассчитать количество ресурса, поступившего в каждый орган дерева, используя в качестве предиктора заранее определённый ранг этого органа:
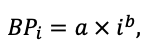
где i — ранг фракции (1 — ствол, включая кору; 2 — скелетные корни; 3 — ветви; 4 — листва или хвоя; 5 — тонкие корни), BPi — доля i-й фракции в общей массе дерева, a и b — эмпирические коэффициенты (Исаев и др., 2007; Komarov et al., 2017b), значения которых рассчитываются на основе диаметра ствола дерева на высоте груди (DBH) и эмпирических коэффициентов (crank, drank, erank, frank). Процедура расчёта распределения биомассы по фракциям также учитывает влияние условий местообитания (Thurm et al., 2017; Weemstra et al., 2017).
При инициализации подмодели абсолютная масса всех фракций вычисляется на основе аллометрического уравнения для биомассы ствола BST, для которой оценки являются наиболее точными (в силу большого числа наблюдений и больших значений измеряемой величины):
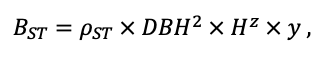
где ρST — видоспецифичная удельная масса ствола в абсолютно сухом состоянии (с учётом коры), кг м−3; DBH — диаметр ствола дерева на уровне груди, м; H — высота дерева, м; z, y — эмпирические коэффициенты. После расчёта массы ствола, исходя из ранее рассчитанной доли ствола, определяется общая масса дерева, на основе которой далее рассчитываются массы всех органов.
Также в подмодели производится расчёт годичного опада (как фиксированной доли биомассы каждой из фракций биомассы) и вычисляется чистый прирост биомассы каждый из фракций (общий прирост за вычетом годичного опада). В случае если чистый прирост общей биомассы принимает отрицательное значение, дерево считается отмирающим (детерминистический компонент смертности). На основе расчётного прироста биомассы ствола вычисляются его приросты в высоту и в диаметре.
Помимо описанного выше детерминистического компонента смертности деревьев, основанного на показателе чистого прироста биомассы, в подмодели реализован стохастический компонент (Seidl et al., 2012), основанный на повышении вероятности гибели дерева по мере приближения его возраста A (лет) к видоспецифичному максимальному значению Amax:
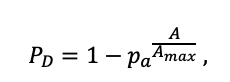
где pa — доля деревьев, достигающих максимального возраста.
Процедура пространственного распределения хвойно-листового опада древесного яруса рассчитывает массу опада листвы или хвои, поступающую в каждую ячейку имитационной решётки. Для каждого дерева рассчитывается пространственное распределение опада (D) в ячейках с координатами (x,y), которое определяется средним радиусом кроны дерева F (CR, рассчитывается в подмодели конкуренции за ФАР) в наиболее широкой её части. Радиус зоны разлёта определяется как видоспецифичная доля от высоты дерева (параметр DLIT):
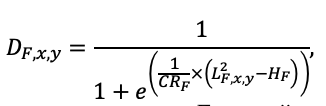
где L — расстояние от центра масс кроны дерева F до ячейки с координатами (x,y). Для учёта влияния микрорельефа пространственное распределение опада корректируется с учётом относительной высоты ячейки (MR) c координатами (x,y):
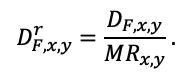
Масса опада дерева F, поступающая в ячейку с координатами (x,y), рассчитывается как
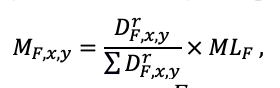
где MLF — масса хвойно-листового опада дерева F.
Для учёта влияния асимметрии кроны каждого дерева на пространственное распределение опада за центр зоны разлёта принимается центр масс проекции кроны дерева, который вычисляется как средневзвешенные координаты (x,y). В качестве весов используется суммарная по вертикальному профилю масса листвы/хвои в ячейке (x,y).
Опад ветвей полагается поступающим равномерно во все ячейки, перекрытые проекцией кроны конкретного дерева; распределение опада скелетных и тонких корней рассчитывается в подмодели корневой конкуренции на основе смоделированной структуры корневых систем и расчётной интенсивности отмирания корней. До завершения разработки усовершенствованной процедуры, пространственное распределение опада стволовой древесины и коры полагается аналогичным распределению опада ветвей.
Живой напочвенный покров
Для моделирования вклада растений живого напочвенного покрова в баланс углерода, азота и динамику лесных экосистем была разработана подмодель eco-CAMPUS, являющаяся модифицированной версией модели CAMPUS-S (Frolov et al., 2020a, 2020b). Подмодель eco-CAMPUS, интегрированная в общую систему моделей, является индивидуально-ориентированной процессной имитационной моделью с пространством, представленным в виде трёхмерной решётки. Подмодель сочетает в себе несколько техник моделирования: клеточно-автоматное (состояние ячейки зависит от состояния соседних) и технику L‑систем (модульное развитие системы клонов). В отличие от модели САMPUS-S, в которой в одной ячейке может быть представлено не более одного растения, eco-CAMPUS допускает присутствие в одной ячейке нескольких растений одного или разных видов, занимающих различные ярусы по высоте (в структуре подмодели предусмотрено 6 ярусов: 0–10, 10–20, 20–30, 30–40, 40–50 и 50–100 см). При этом одно растение может занимать более одной ячейки в соответствии с морфологическим строением, изменяющимся в течение жизненного цикла. Поскольку подмодель предназначена для анализа динамики популяции как клональных, так и неклональных растений, для обозначения элементарной учётной единицы при моделировании используется термин «растительная единица» (РЕ), которая представляет собой либо парциальное образование в составе клонального растения (т. е. побег вместе с корневищем), либо отдельную особь неклонального растения. Развитие растений во времени учитывается в подмодели через их онтогенетические состояния (Evstigneev, Korotkov, 2016). Для каждого из онтогенетических состояний (ОС) задана соответствующая площадь проекции надземной и подземной части, высота надземной части растения, высота прикрепления фотосинтезирующих органов. Каждое онтогенетическое состояние имеет свою продолжительность, а все переходы являются вероятностными. Временной шаг подмодели составляет 1 день.
На этапе инициализации в каждую ячейку помещается набор РЕ из заданного списка видов. Соотношение РЕ в ячейке и их суммарное проективное покрытие (доля занятой площади в ячейке) определяется коэффициентом оптимальности условий (обобщённый отклик продуктивности на комплекс экологических факторов). Онтогенетические состояния и абсолютные возраста РЕ задаются вероятностно с учётом начального онтогенетического спектра, являющегося входным параметром.
Единичный шаг подмодели состоит из нескольких последовательно выполняющихся операций. Увеличение возраста происходит ежедневно для каждой РЕ. При этом как абсолютный, так и относительный возраст (продолжительность пребывания РЕ в текущем ОС) увеличиваются на величину, обратную продолжительности вегетационного периода. Использование долей вегетационного периода вместо календарных дней позволяет моделировать динамику популяций видов с широким географическим ареалом, произрастающих в разных широтах. Когда РЕ достигает относительного возраста, равного продолжительности текущей онтогенетической стадии, переход РЕ на другую онтогенетическую стадию рассчитывается вероятностно. Вероятность последовательного перехода в следующую стадию онтогенеза (Ptr) считается равной отношению потенциального прироста (прироста в оптимальных условиях за период пребывания в текущем ОС) к фактическому. Вероятность гибели РЕ рассчитывается как (1 − Ptr). В случае смены онтогенетического состояния изменяется диаметр, высота РЕ (занимаемый ярус) и высота прикрепления фотосинтезирующих органов, а также максимальный радиус зоны корневого питания. Площадь листьев РЕ рассчитывается как произведение биомассы и удельной площади листьев. Относительная площадь листьев РЕ (LADFGV) рассчитывается как отношение площади листьев РЕ к площади проекции её фотосинтезирующих органов и распределяется между занимаемыми РЕ ярусами. В подмодели в явном виде не представлено расположение отдельных РЕ внутри ячейки. Поэтому при увеличении размера побеговой системы возрастает доля, занимаемая РЕ в текущей либо в одной из соседних ячеек. Вероятность того, в какой из ячеек увеличится доля данной РЕ, прямо пропорциональна коэффициенту оптимальности условий и обратно пропорциональна проективному покрытию в ячейке. Количество семян на моделируемой территории рассчитывается как произведение числа РЕ в генеративном ОС каждого вида и видоспецифичного числа семян на одну РЕ и распределяется между ячейками случайным образом один раз за вегетационный период (по достижении максимальной доли генеративных органов в общей биомассе).
При расчёте продукции биомассы РЕ учитываются те же факторы и ресурсы, которые используются в подмодели расчёта продукции биомассы древостоя. Конкуренция за свет между РЕ в ячейке реализована исходя из допущения, что лучи света, прошедшего под полог, ориентированы преимущественно вертикально и последовательно проходят через все ярусы живого напочвенного покрова, а ослабление их интенсивности происходит экспоненциально. Расчёт коэффициента ослабления ФАР на каждом ярусе производится по следующей методике (Campbell, 1986). Для каждой РЕ рассчитывается коэффициент ориентации листьев (Xi) как отношение длины горизонтальной к протяжённости вертикальной проекции фотосинтезирующих органов, который используется для расчёта коэффициента ослабления ФАР ( ![]() ):
):
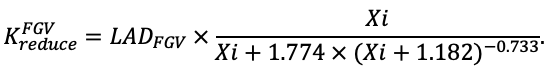
Ослабление ФАР в ячейке на каждом из ярусов вычисляется как экспонента произведения суммы коэффициентов ослабления ФАР всех РЕ, представленных в данном ярусе ячейки, на длину пути луча в ярусе. Перехваченная ФАР в ярусе рассчитывается как разность плотностей потока ФАР на верхней и нижней границе и распределяется между РЕ, представленными в ярусе, пропорционально их коэффициентам ослабления ФАР. Конкуренция за доступный азот и доступную почвенную влагу, а также расчёт продукции биомассы происходит в соответствии с алгоритмами, аналогичными таковым для деревьев (описаны в соответствующих подразделах). Распределение биомассы между органами РЕ происходит неравномерно в течение вегетационного периода. С момента, когда все органы РЕ (листья, вегетативные побеги, генеративные побеги, корневища и тонкие корни) полностью сформированы, для описания распределения прироста биомассы используется уравнение рангового распределения (Frolov et al., 2022). До этого момента прирост биомассы распределяется между теми органами, чьи доли в общей биомассе оказываются ниже, чем определённые ранговым распределением. В случае если РЕ находится в генеративном ОС, сначала прирастает биомасса вегетативных органов, и только после достижения ими необходимой доли в общей биомассе начинается прирост генеративных органов. Опад листьев и побегов происходит в последний день вегетационного периода, опад тонких корней — ежедневно, корневища отмирают только вместе с РЕ. Доли от массы органов, поступающие в опад, являются входным параметром подмодели. Перед опаданием фотосинтезирующих органов у многолетних растений производится резорбция азота с его добавлением в орган, имеющий максимальную биомассу.
Водный режим растительности и гидротермический режим почвы
При моделировании влажности почвы использован простой балансовый подход. Очевидно, изменение влагосодержания деятельного слоя почвы ΔW = W2 − W1 можно принять равным
![]()
где r — осадки, E — эвапотранспирация (суммарное испарение), f — сток, W1 и W2 — запасы влаги в начале и конце шага моделирования.
При моделировании процессов, связанных с пространственной неоднородностью экологических условий в лесу, наиболее целесообразным является дифференцированный подход к рассмотрению испарения различными элементами леса, что позволяет учесть их влияние на динамику влаги. В этом случае эвапотранспирация представляется в виде суммы трёх слагаемых (Фёдоров, 1977):
![]()
где Et — транспирация древостоя; Ei — испарение задержанных пологом леса атмосферных осадков; Es — испарение с напочвенного покрова.
Количество воды ETS, изымаемое из ячейки почвы с координатами (x,y,z) в процессе транспирации, вычисляется с учётом пространственного распределения биомассы тонких корней деревьев mFR(x,y,z,n):
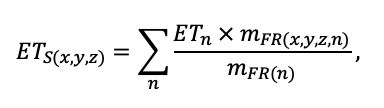
где
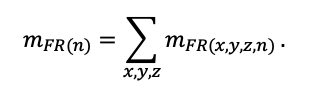
Количество воды ETC(x,y,z,), выделяемое листьями в процессе транспирации, вычисляется с учётом пространственного распределения биомассы листьев деревьев mLV(x,y,z,n):
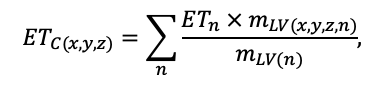
где
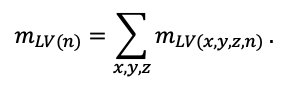
Вычисление потенциальной эвапотранспирации PET производится с использованием следующей зависимости:
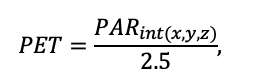
где 2.5 МДж кг−1 — удельная теплота испарения воды.
Вычисление суммарной площади листвы и ветвей деревьев, приходящихся на ячейку проекции полога, производится по формуле
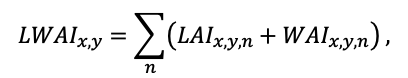
где LAI — индекс листовой поверхности, WAI — индекс поверхности ветвей (м2 м−2).
На основе LWAI вычисляется водоудерживающая способность крон CSCx,y (Dickinson, 1984):
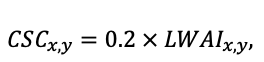
Количество задержанных пологом леса осадков определяется с использованием выражения, предложенного Ю. В. Карпечко (1997):
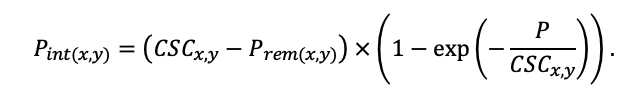
Фактическое содержание воды в пологе Pcurr(x,y) рассчитывается как сумма перехваченных осадков, воды, оставшейся с предыдущего шага Prem(x,y), и воды, выделившейся в результате транспирации (либо гуттации):
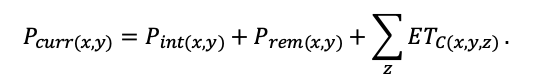
Испарение воды пологом Estand(x,y) рассчитывается как минимальное значение из потенциальной эвапотранспирации и содержания воды в пологе:
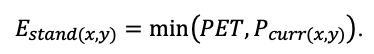
Сток воды с листьев и ветвей DripLV(x,y) рассчитывается как разность текущего запаса в пологе, испарения из полога и ёмкости полога:
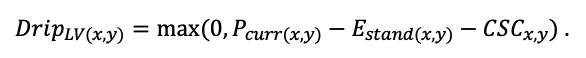
Количество воды, оставшейся в пологе на следующий шаг, Prem, вычисляется как
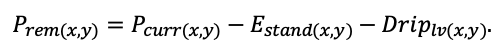
Испарение воды напочвенным покровом рассчитывается по (Williams, Flanagan, 1996; Daikoku et al., 2008):
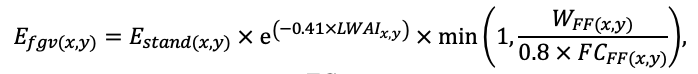
где WFF — запас влаги в подстилке, FCFF — его значение при наименьшей полевой влагоёмкости.
Количество осадков, прошедших под полог, Pbc(x,y), рассчитывается по формуле
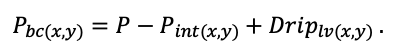
Снег в подмодели представлен тремя фракциями: свежим (SWEf), промёрзшим (SWEi) и протаявшим (SWEw), запас воды в которых представлен водным эквивалентом. Количество осадков, пришедших в твёрдой фазе Psol, рассчитывается по формуле (Grossi et al., 2017):
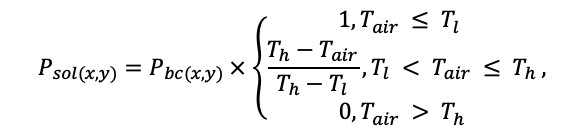
где Th = +2 °C, Tl = 0 °C.
При расчёте таяния снега и льда использовался модифицированный метод расчёта температурного индекса, учитывающий температуру воздуха и приходящую коротковолновую радиацию (Pelliссiotti et al., 2005):
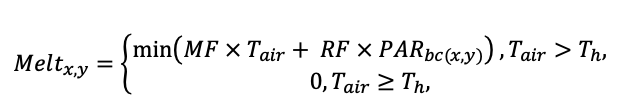
где MF = 1.2 мм день−1 °C−1, RF составляет 2.61 м2 мм МДж−1 (Pelliссiotti et al., 2005). В подмодели предполагается, что первым протаивает свежий снег:
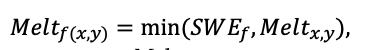
если его количество оказывается меньше Meltx,y, начинает протаивать лёд:
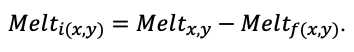
Промерзание считается с использованием классического метода температурного индекса (Finsterwalder, 1887):
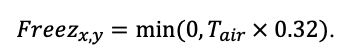
Когда содержание жидкой воды в слое снега превышает его водоудерживающую способность, избыток воды перетекает в нижележащий слой. Водоудерживающая способность снега WHC рассчитывается по уравнению, предложенному (Pahaut, 1975):
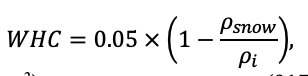
где ρsnow — плотность снега (кг м−3), ρi — плотность льда (917 кг м−3).
Количество воды, которая попадает на почву, liqflow(x,y), рассчитывается как
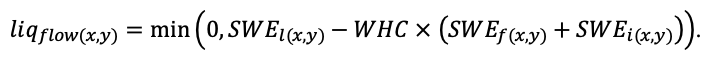
Запас воды в фракции свежего снега (SWEf):
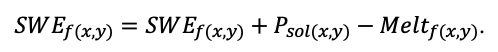
Запас воды в фракции льда (SWEi):
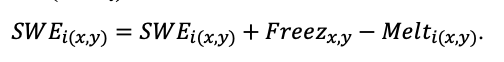
Запас воды в жидкой фракции (SWEw):
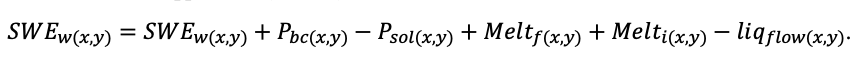
Плотность выпадающего снега (кг м−3) рассчитывается по уравнению (Parajuli et al., 2020):
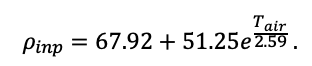
Плотность фракции свежего снега (кг м−3) рассчитывается по формуле:
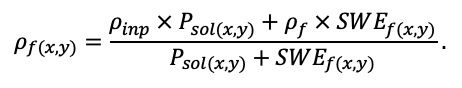
Общая плотность снега (кг м−3) рассчитывается как
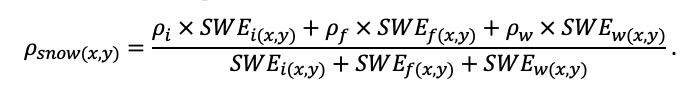
Высота снежного покрова (м) рассчитывается как
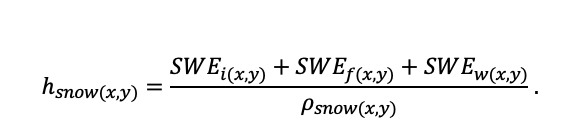
Теплопроводность TCsnow(x,y), теплоёмкость HCsnow(x,y) и температуропроводность TDsnow(x,y) снега рассчитывается по формулам (Yen, 1962, 1981):
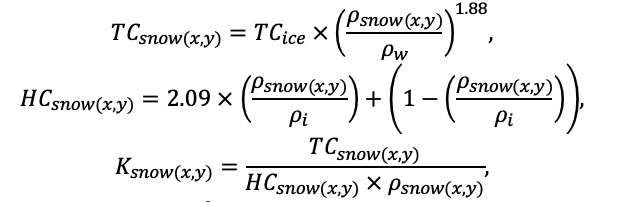
где ρw — плотность воды (1000 кг м−3).
Концентрация органического вещества почвы OMconc(x,y,z) рассчитывается как отношение массы органического вещества mOF(x,y,z) к суммарной массе почвы в ячейке:
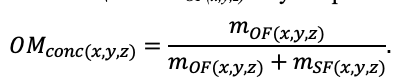
Плотность твёрдой фазы слоя почвы в ячейке рассчитывается как
![]()
где 1.35 и 2.65 (г см−3) — значения плотности органического вещества и минеральных частиц почвы, соответственно. Влажность устойчивого завядания, WP и наименьшая полевая влагоёмкость FC в ячейке (x,y,z) рассчитываются по уравнениям, предложенным В. Балландом с соавторами (Balland et al., 2008), и пересчитанным нами в объёмные единицы влажности (м3 м−3):
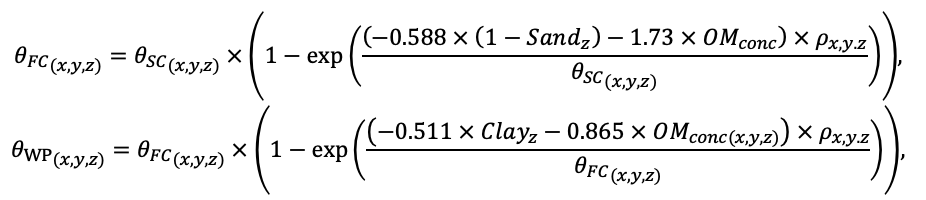
где Sand — содержание песка (частиц размером > 0.05 мм), Clay — глины (< 0.002 мм), в массовых долях (кг кг−1), SC — полная влагоёмкость (общая порозность), м3 м−3:
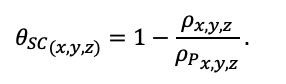
Соответствующие значения запасов влаги в слое Δz, соответственно, равны
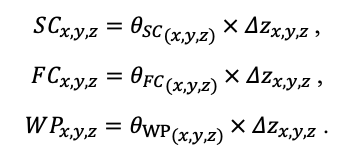
Насыщенная гидравлическая проводимость HCsat(z) вычисляется по (Campbell, 1985):
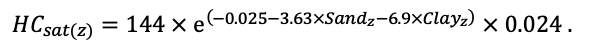
Ненасыщенная гидравлическая проводимость HCx,y,z вычисляется по (Campbell, 1974):
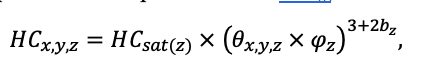
где θx,y,z — влажность почвы (м3 м−3), φ и b — коэффициенты, вычисляемые согласно (Cosby et al., 1984):
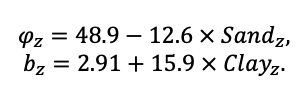
Поскольку ненасыщенная гидравлическая проводимость в разных ячейках почвенного профиля может быть неоднородной и изменяется нелинейно, для расчёта переноса влаги используется среднее логарифмическое ненасыщенных гидравлических проводимостей соседних ячеек:
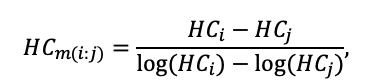
где HCi и HCj — ненасыщенные гидравлические проводимости соседних ячеек. Вычисление запасов воды в каждом слое почвы происходит последовательно сверху вниз на каждом шаге подмодели. Количество воды, протекающей в нижележащий слой почвы, рассчитывается по формуле:
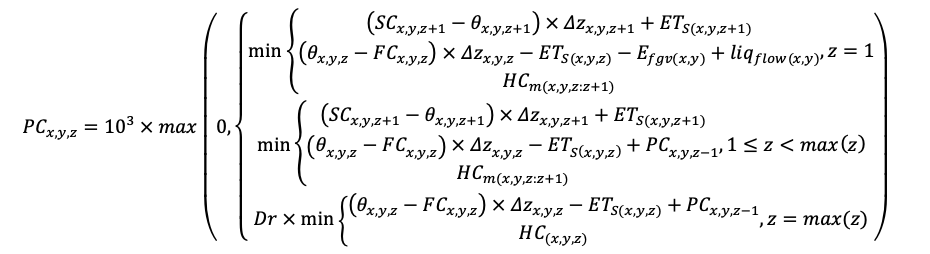
где Dr считается равным 1 при хорошей и 0 — при плохой дренированности.
Запас влаги в слое почвы рассчитывается по формуле:
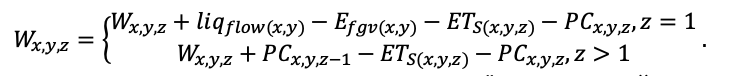
Потенциальные потоки воды в каждом из четырёх направлений в горизонтальной плоскости (вперёд, назад, вправо и влево, зависят от гидравлического градиента, равного синусу угла уклона, и вычисляются как
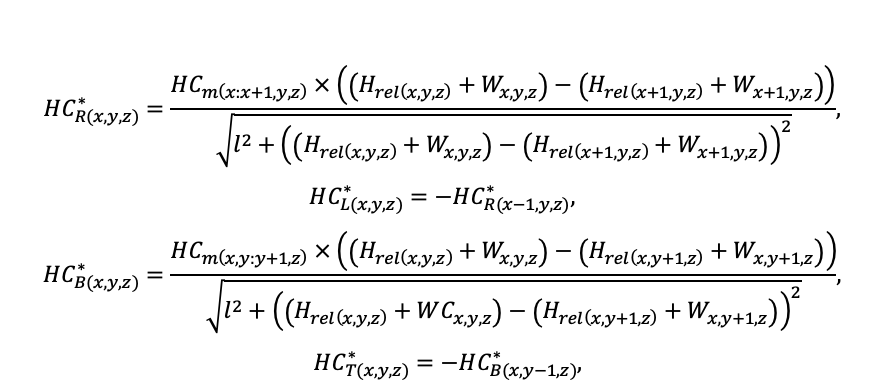
где Hrel — относительная высота ячейки, обусловленная микрорельефом (м), l — горизонтальный размер ячейки (м), пространство завёрнуто на тор.
Суммы положительных (HC+) и отрицательных (HC−) потоков рассчитываются для каждой ячейки (x,y,z):
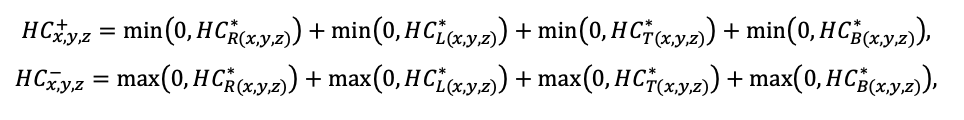
Веса положительных (исходящих) и отрицательных (входящих) потоков в ячейке рассчитываются независимо:
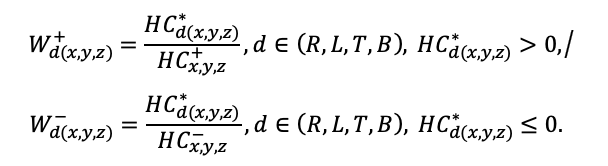
где d соответствует направлению каждого из четырёх потоков. Лимитирование положительных потоков определяется разностью запаса воды в ячейке и полевой влагоёмкости:
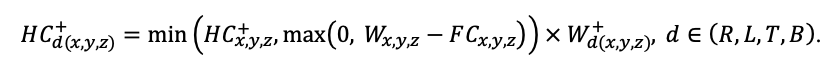
Лимитирование отрицательных потоков определяется разностью полной влагоёмкости и запаса воды в ячейке:
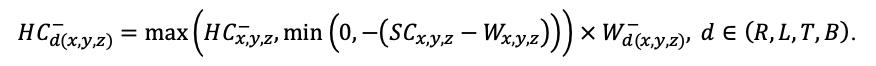
Результирующие потоки (PCR, PCL, PCT, PCB) рассчитываются как наименьшее между положительными и комплементарными им отрицательными потоками, взятыми по модулю:
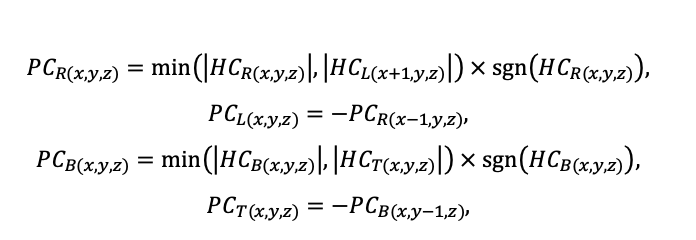
где sgn(HCdЄ(R,L,T,B)) — индикатор знака потока HCdЄ(R,L,T,B) (равен +1, если поток положительный и −1, если отрицательный). Запас воды в ячейке после латерального переноса ( ) рассчитывается как разность запаса воды в ячейке и потоков в четырёх направлениях:
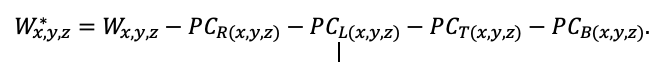
Объёмная влажность слоя почвы в ячейке вычисляется как
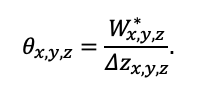
Температура почвы (Ts) влияет на большинство почвенных процессов, а также на рост растений. Вместе с химическими и физическими характеристиками органического вещества почвы, температура почвы является одной из основных переменных, контролирующих биологическую активность почвы (например, Lundegårdh, 1927; Kätterer et al., 1998; Frank et al., 2002). Следовательно, пространственно-детализированный прогноз динамики температуры почвы необходим для применения других подмоделей, таких как подмодель динамики органического вещества почвы (ОрВП). К сожалению, пространственно-детализированные данные о температуре почвы доступны редко (Schaetzl et al., 2005), и их приходится оценивать на основе другой информации, обычно стандартных метеорологических данных.
Большинство моделей Ts основаны на теориях теплообмена в почве и баланса энергии на её поверхности (Nobel, Geller, 1987; Rankinen et al., 2004; Chalhoub et al., 2017). Теоретическое моделирование баланса энергии обычно включает солнечное излучение (поглощённое и отражённое), инфракрасное излучение (входящее и исходящее), энергию турбулентного потока (скрытое и явное тепло) и поток тепла через поверхность в нижележащие слои почвы (Mihalakakou et al., 1997; Chalhoub et al., 2017). Для модели, основанной на балансе энергии, обычно требуются более подробные параметры приповерхностных слоёв и почвы, такие как величины турбулентного потока, чтобы сделать модель надёжной и точной; однако определение величин турбулентного потока — нетривиальная задача (Dhungel et al., 2021; Kutikoff et al., 2021). В связи с этим были разработаны более простые эмпирические модели с меньшим количеством динамических параметров для моделирования Ts (Zheng et al., 1993; Kang et al., 2000; Plauborg, 2002; Liang, Uchida, 2014; Badache et al., 2016). Однако эти эмпирические модели могут привести к относительно большим ошибкам, превышающим 2 °C, из-за отсутствия детального учёта физических процессов в почве и атмосфере (Badía et al., 2017). В связи с этим, оптимальным подходом к созданию надёжной и легко параметризуемой модели для пространственно-детализированной оценки температуры почвы в неоднородных условиях представляется объединение принципов физики теплопередачи с эмпирическими моделями, описывающими влияние растительности на Ts.
В нашей подмодели для расчёта температуры почвы используется одномерное уравнение теплопроводности (в предположении, что горизонтальные градиенты температуры, а следовательно, и потоки тепла в почве, значительно меньше вертикальных) с простыми параметризациями теплофизических свойств. В качестве граничных условий на верхней границе принимается температура поверхности, вычисляемая через температуру воздуха и затенение пологом. На нижней границе — постоянная температура (для чего глубина слоя расчёта температуры принимается равной 12.8 м). Уравнение аппроксимировано неявной конечно-разностной схемой и решается методом прогонки (Патанкар, 1984).
Температуропроводность в каждой ячейке (Kx,y,z, м2 с−1) вычисляется по функции, предложенной Т. А. Архангельской (2012):
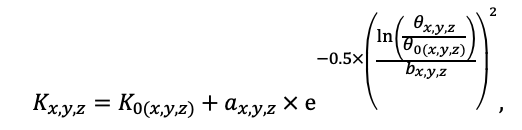
где K0 — температуропроводность сухой почвы; θ0 — объёмная влажность, при которой достигается максимум температуропроводности; K0 + a — максимальная температуропроводность при θ = θ0; b — параметр, характеризующий ширину пика кривой и определяющийся диапазоном влажности, в котором происходит активный термоперенос почвенной влаги. Указанные параметры для органоминеральных горизонтов могут быть выражены через плотность почвы и содержание в ней органического углерода (Лукьященко, Архангельская, 2018):
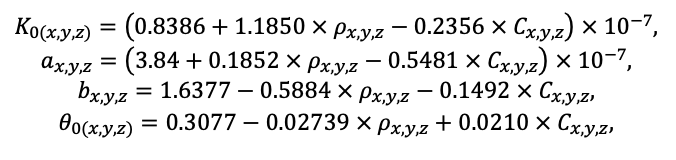
где С — концентрация углерода (%). Соответствующие параметры для органогенного горизонта почвы были приняты константами в соответствии с работой Т. А. Архангельской и А. А. Гвоздковой (Arkhangelskaya, Gvozdkova, 2019). Расчёт температуропроводности снега описан выше.
Динамика пулов органического вещества почвы
В систему моделей интегрирована подмодель динамики органического вещества почв Romul_Hum (Chertov et al., 2017a, 2017b; Komarov et al., 2017a). Это новая версия почвенной модели ROMUL, которая подробно описана ранее (Chertov et al., 2001; Моделирование динамики …, 2007). Основное отличие модели Romul_Hum от исходной модели ROMUL заключается в новой процедуре расчёта динамики азота. В ROMUL, как и в большинстве других моделей, динамика азота была строго привязана к путям трансформации углерода почвенного органического вещества (ОВ), а для расчёта пулов азота использовались эмпирические поправочные коэффициенты к скоростям трансформации углерода. В модели Romul_Hum дополнительно реализованы процедуры, описывающие трансформацию С и N в пищевых сетях почвенной микро-, мезофауны и дождевых червей. Побочными продуктами жизнедеятельности почвенной фауны, помимо выдыхаемого С-СО2, являются органическое вещество экскрементов, копролитов и мортмассы и минеральный азот (преимущественно аммоний) жидких экскретов, что позволило более детально рассчитывать в Romul_Hum продукцию минерального азота почвы.
Структура модели Romul_Hum отражает функциональную активность трёх сообществ почвенных организмов-деструкторов. ОВ представлено в модели каскадом фракций, которые в целом соответствуют органогенным подгоризонтам почвы (L — свежий поверхностный опад; F — частично разложившийся ферментированный опад; H — гумифицированный горизонт лесной подстилки) и гумусово-аккумулятивному горизонту минеральной почвы Ah/Ahe. Скорость минерализации в каждом пуле была определена экспериментально и зависит от химических свойств органического вещества, влажности и температуры почвы (Моделирование динамики …, 2007).
Динамика пулов углерода и азота в каждой ячейке описывается следующей системой уравнений:
где — запас углерода в когорте k пула L на шаге i, — углерод, поступающий в когорту k с опадом, — поток углерода из когорты k пула L в пул F, — поток С‑CO2 из когорты k пула L.
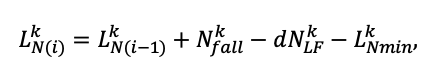
где — запас азота в когорте k пула L на шаге i, — азот, поступающий с опадом, — поток азота из когорты k пула L в пул F, — поток минерализованного азота из когорты k пула L.
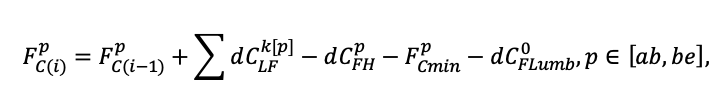
где — запас углерода в когорте p (органогенном и органоминеральном горизонтах) пула F на шаге i, — поток С-CO2 из когорты p пула F, — поток углерода, потребляемого дождевыми червями из надземной когорты F; ab, be — здесь и далее: индексы, показывающие, относится данный пул/поток к наземному или подземному.
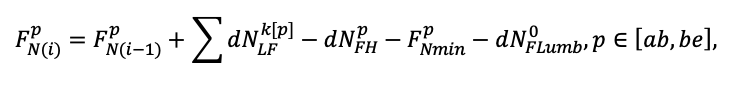
где — запас азота в когорте p (органогенном и органоминеральном горизонтах) пула F на шаге i, — поток минерализованного азота из когорты p пула F, — поток азота, потребляемого дождевыми червями из надземной когорты F.
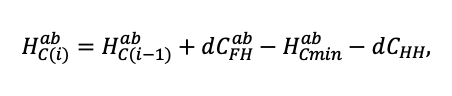
где – запас углерода в пуле H органогенного горизонта на шаге i, — поток С‑CO2 из пула H органогенного горизонта, dCHH — поток углерода из пула H органогенного горизонта в органоминеральный.
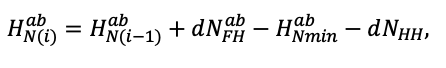
где – запас азота в пуле H органогенного горизонта на шаге i, — поток минерализованного азота из пула H органогенного горизонта, dNHH — поток азота из пула H органогенного горизонта в органоминеральный.
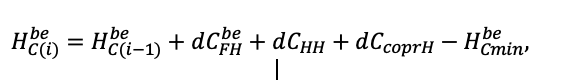
где — запас углерода в пуле H органоминерального горизонта на шаге i, — поток С‑CO2 из пула H органоминерального горизонта, dCCoprH — поток углерода из копролитов дождевых червей в пул H органоминерального горизонта.
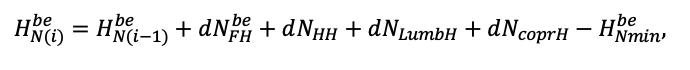
где – запас азота в пуле H органоминерального горизонта на шаге i, — поток минерализованного азота из пула H органоминерального горизонта, dNcoprH — поток азота из копролитов дождевых червей в пул H органоминерального горизонта, dNLumbH — поток азота из мортмассы дождевых червей в пул H органоминерального горизонта.
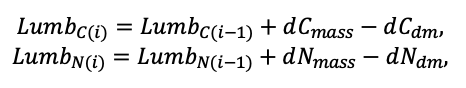
где LumbC(i) и LumbN(i) — углерод и азот биомассы дождевых червей, dCmass и dNmass — прирост углерода и азота биомассы дождевых червей, dCdm и dNdm– углерод и азот мортмассы дождевых червей.
Минерализация и гумификация пула L описывается следующим образом:
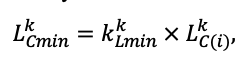
где — коэффициент минерализации ОВ когорты k пула L.
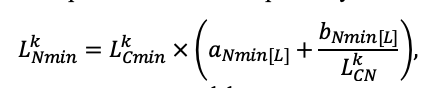
где aNmin[L] и bNmin[L] — эмпирические коэффициенты, характеризующие соотношение и активность бактериальной и грибной компоненты микробного сообщества; — отношение C:N когорты k пула L.
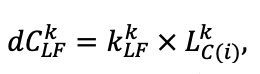
где — коэффициент гумификации ОВ когорты k пула L.
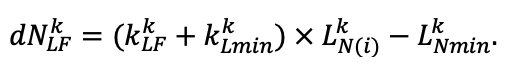
Минерализация и гумификация пула F описывается следующим образом:
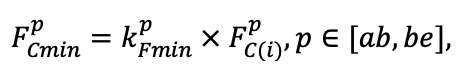
где — коэффициент минерализации ОВ когорты p пула F.
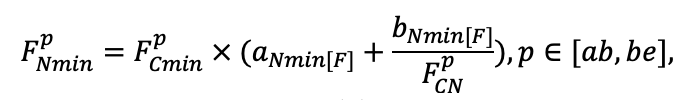
где aNmin[F] и bNmin[F] — эмпирические коэффициенты, характеризующие соотношение и активность бактериальной и грибной компоненты микробного сообщества; — отношение C:N когорты p пула F.
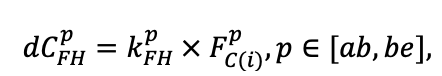
где — коэффициент гумификации ОВ когорты p пула F.
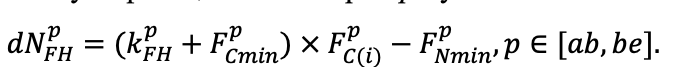
Потоки углерода и азота, потребляемые дождевыми червями из пула F, рассчитываются как
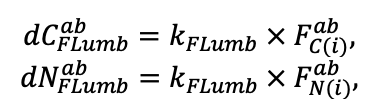
где kFLumb — коэффициент пищевой активности дождевых червей.
Минерализация и гумификация пула H описывается следующим образом:
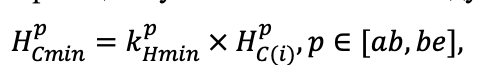
где — коэффициент минерализации ОВ когорты p пула H.
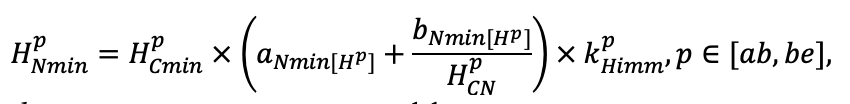
где aNmin[F] и bNmin[F] — эмпирические коэффициенты, характеризующие соотношение и активность бактериальной и грибной компоненты микробного сообщества, — коэффициент иммобилизации азота из пула H (равен 1.0 для органогенного горизонта и 0.7 для органоминерального).
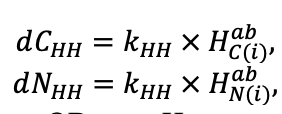
где kHH — коэффициент гумификации ОВ пула H органогенного горизонта.
Жизнедеятельность дождевых червей описывается следующей системой уравнений:
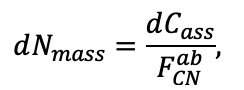
где dCass — ассимилированная часть потреблённого дождевыми червями углерода, который вычисляется по уравнению
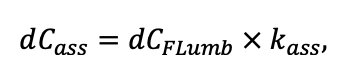
где kass — коэффициент ассимиляции.
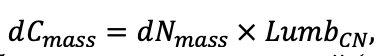
где LumbCN — отношение C:N биомассы дождевых червей (принято равным 4).
Возвращённая в почву с копролитами часть потреблённого червями углерода вычисляется по уравнению
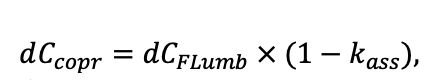
и, соответственно, часть потреблённого червями азота — по уравнению:
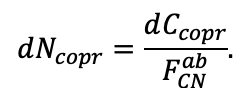
Масса С‑CO2, высвободившаяся в результате минерализации копролитов дождевых червей, вычисляется как
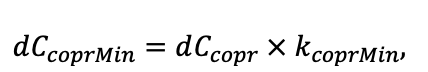
где kcoprMin — коэффициент минерализации копролитов. Азот при минерализации копролитов вычисляется по уравнению
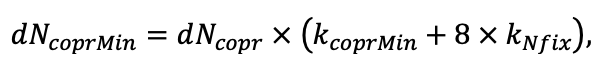
где kNfix — коэффициент азотфиксации, принятый равным 1.014 × 10−6 (Komarov et al., 2017a).
Количества углерода и азота, поступающих из копролитов дождевых червей в пул H, вычисляются по уравнениям:
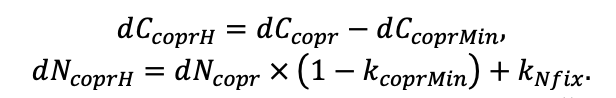
Содержание углерода и азота в мортмассе дождевых червей вычисляются как
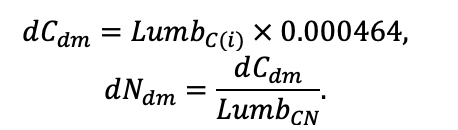
Количество азота поступающих из мортмассы червей в пул H органоминерального горизонта вычисляется как
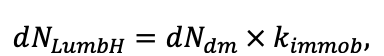
где kimmob — коэффициент иммобилизации азота.
С‑CO2 дыхания дождевых червей вычисляется как
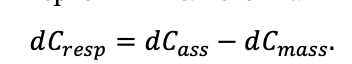
Суммарная эмиссия С-CO2 за счёт жизнедеятельности дождевых червей рассчитывается как
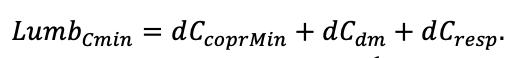
Суммарное выделение азота в минеральных формах, происходящее в результате жизнедеятельности дождевых червей, рассчитывается как
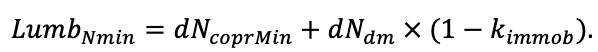
Численные значения коэффициентов и поправок в уравнениях заимствованы из описания модели Romul_Hum (Komarov et al., 2017a; Chertov et al. 2017a, 2017b) или скомпилированы по другим источникам (Моделирование динамики …, 2007).
Коэффициент минерализации пула L органогенных горизонтов вычисляется как
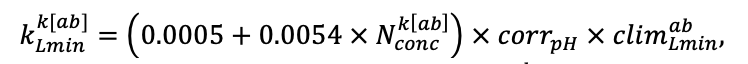
где — концентрация азота в когорте опада k; — (здесь и далее) поправка на температуру и влажность почвы, corrpH — поправка на pH почвы, которая вычисляется как
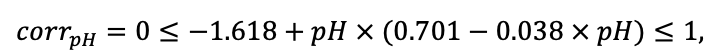
где pH — величина pH почвы.
Коэффициент минерализации пула L органоминеральных горизонтов вычисляется как
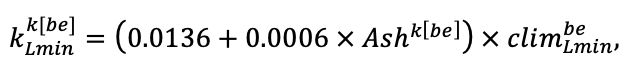
где Ashk[be] — зольность органического вещества в когорте опада k.
Коэффициент гумификации пула L органогенных горизонтов рассчитывается по уравнению
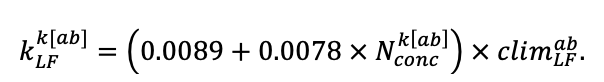
Коэффициент гумификации пула L органоминеральных горизонтов вычисляется как
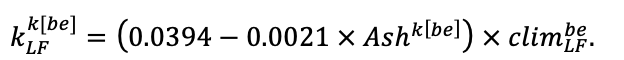
Коэффициент пищевой активности дождевых червей рассчитывается по уравнению
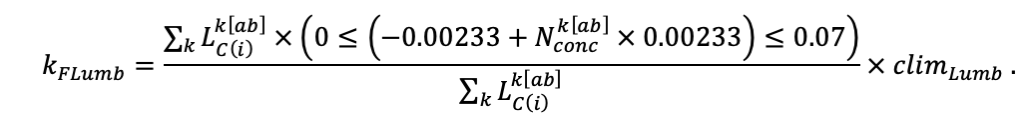
Коэффициент ассимиляции пищи дождевыми червями рассчитывается как

Коэффициент минерализации свежих копролитов дождевых червей вычисляется по уравнению
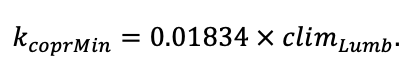
Коэффициенты минерализации пулов F органогенных и органоминеральных горизонтов рассчитываются по уравнениям:
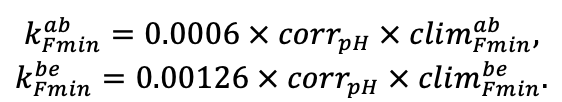
Коэффициенты гумификации пулов F органогенных и органоминеральных горизонтов рассчитываются по уравнению
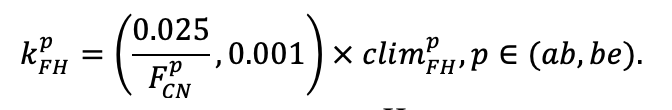
Коэффициенты минерализации пулов H органогенных и органоминеральных горизонтов рассчитываются по уравнениям:
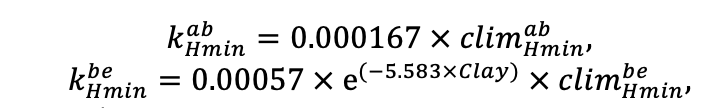
где Clay — доля илистой фракции.
Коэффициент гумификации пула H органогенного горизонта вычисляется как
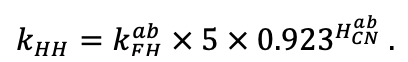
Для расчёта поправок коэффициентов на влажность почвы используется значение влажности почвы, нормированное на полевую влагоёмкость:
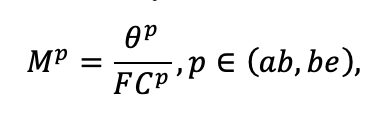
где — объёмная влажность горизонтов p, FCp — полевая влагоёмкость горизонта p.
Поправка на влажность почвы для расчёта коэффициента минерализации пулов L, F, H ( , и соответственно) и коэффициента гумификации пула L ( ) вычисляется как
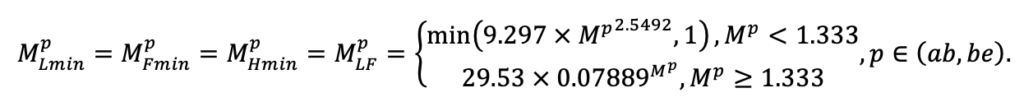
Для расчёта поправки коэффициента гумификации пула F используется следующее уравнение:
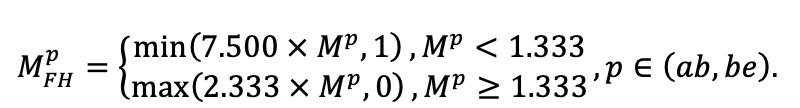
Поправка на влажность почвы коэффициента активности дождевых червей рассчитывается как
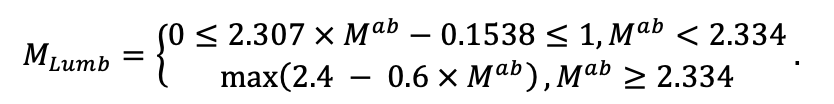
Поправка на температуру почвы для расчёта коэффициента минерализации пула L вычисляется по уравнению
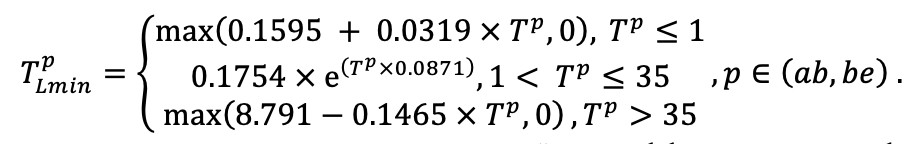
Поправка на температуру почвы для расчёта коэффициента гумификации пула L вычисляется как
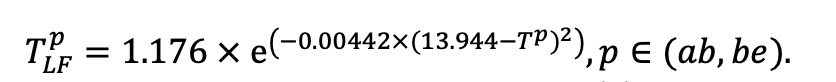
Поправка на температуру почвы для расчёта коэффициента минерализации пула F вычисляется по уравнению
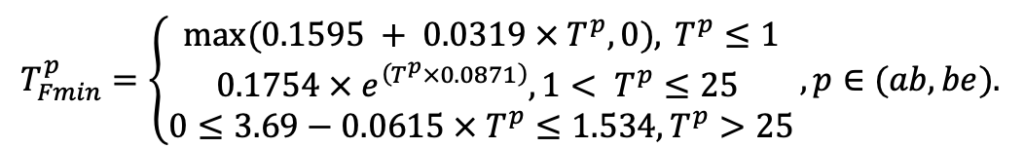
Поправка на температуру почвы для расчёта коэффициента гумификации пула F вычисляется по уравнению
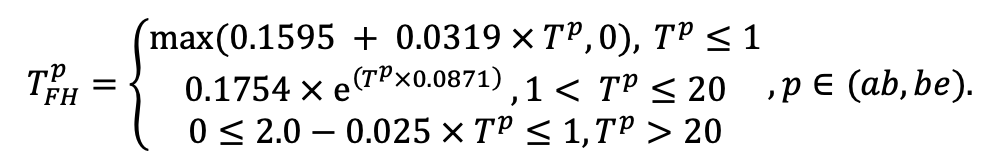
Поправка на температуру почвы для расчёта коэффициента минерализации пула H вычисляется по уравнению
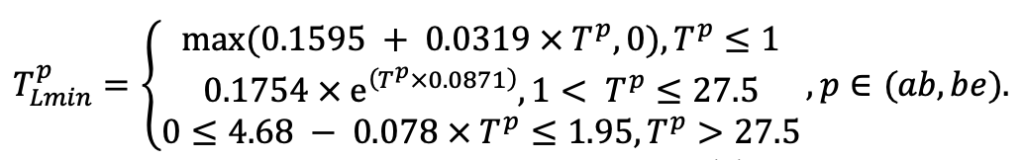
Поправка на температуру почвы для расчёта коэффициента активности дождевых червей рассчитывается как
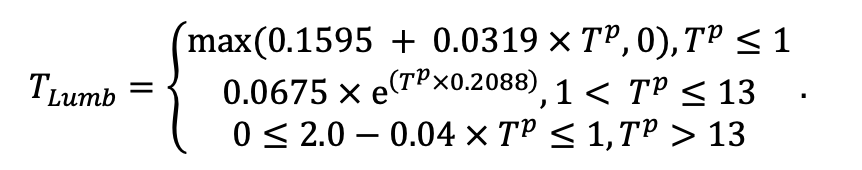
Результирующие климатические поправки, используемые при расчёте коэффициентов, вычисляются как произведение поправок на температуру и на влажность почвы.
Разложение крупных древесных остатков (КДО) в текущей версии системы моделей описывается с помощью тех же процедур, что и разложение недревесных фракций опада.
Блок имитации рубок
Данный блок позволяет имитировать различные виды рубок на основании заданных внешних параметров, к основным из которых относятся интенсивность рубок (изъятие древесины и остальных фракций фитомассы) и способы отведения деревьев в рубку. Интенсивность изъятия может определяться либо долей от значения контрольного показателя (сумма площадей сечений, м2 га−1, или густота древостоя, шт. га−1) до рубки, либо целевым значением контрольного показателя, которое должно быть достигнуто после проведения рубки. Способ отведения деревьев в рубку основан на их сортировке по диаметру ствола на уровне груди: в зависимости от параметра, отведение в рубку будет производиться либо по убыванию данного показателя (т. е. вырублены будут наиболее крупные деревья), либо по возрастанию (первыми в рубку будут отведены тонкомерные деревья), либо в рубку будут случайным образом отобраны деревья из всех ступеней толщины. Дополнительно можно задать долю наиболее крупных деревьев, которые не будут отведены в рубку, и пороговое значение диаметра ствола на уровне груди, ниже которого деревья не будут отводиться в рубку, даже если не достигнута требуемая интенсивность изъятия. Расширенные алгоритмы отвода деревьев в рубку предусматривают оптимизацию прореживания древостоев таким образом, чтобы снизить конкуренцию между деревьями за ресурсы. Для оценки интенсивности конкуренции используется индекс отношения размеров к расстоянию, показавший хорошие результаты при минимальной ресурсоёмкости вычислений (Shanin et al., 2021a). Параметры процедуры позволяют указать порядок, в котором деревья разных видов будут отводиться в рубку, а также заблокировать отведение в рубку деревьев определённых видов. Также предусмотрена возможность имитации оставления на участке порубочных остатков, которые далее прибавляются к количеству растительного опада и передаются в подмодель динамики органического вещества почвы. Подсадка деревьев в существующий древостой имитируется той же процедурой, что и начальное размещение, но с учётом уже занятых деревьями ячеек.
Перспективные направления совершенствования системы моделей
Цель любой модели заключается в том, чтобы обеспечить максимально точное воспроизведение основных экосистемных процессов при минимизации количества необходимых входных параметров (избегая в первую очередь необходимости использования трудно определяемых объект-специфичных параметров). На наш взгляд, некоторые улучшения могут быть внесены в систему моделей.
В первую очередь необходим блок имитации естественного возобновления. В имитационных экспериментах с текущей версией системы моделей мы использовали для этого процедуру, аналогичную процедуре имитации начального размещения деревьев с использованием экспертной оценки густоты и видового состава естественного возобновления. Ранее (Juutinen et al., 2018; Shanin et al., 2021b) нами использовались эмпирические модели возобновления (Pukkala et al., 2012). Однако оценка параметров данных моделей была проведена на основе ограниченного набора экспериментальных данных, что не гарантирует их точности в других эколого-географических условиях. Решением может разработка процессной модели возобновления, которая учитывает семенную продуктивность деревьев в зависимости от условий местообитания, распространение семян по имитируемой площадке (в т. ч. возможность заноса семян видов, не представленных на имитируемой площадке в данный момент) и вероятность успешного приживания и выживания подроста в зависимости от локальных условий (освещённость под пологом, влажность, наличие растений ТКЯ). Также данная подмодель должна включать возможность имитации вегетативного размножения, используя данные о распространении корневых систем и интенсивности образования корневых отпрысков.
Как подмодель возобновления, так и процедура имитации начального размещения деревьев могут быть усовершенствованы за счёт включения более сложных процедур, учитывающих кластеризацию в пространстве деревьев одного или разных видов (Pommerening, Grabarnik, 2019). Для расширения спектра возможных имитационных сценариев необходимо включение в систему моделей процедур, имитирующих разные виды нарушений: пожары, ветровалы, воздействие фитопатогенов и загрязнения. Уже имеющаяся процедура имитации рубок может быть улучшена за счёт внедрения оптимизационных процедур (Tahvonen, Rämö, 2016), позволяющих автоматически подобрать параметры рубки для максимизации целевого показателя, в качестве которого может выступать максимальный доход, накопление углерода и т. д. Кроме того, оптимизационный алгоритм отведения деревьев в рубку может использовать вместо упрощённого индекса конкуренции выходные данные подмоделей конкуренции (т. е. количество полученных каждым деревом ресурсов) для расчёта оптимального прореживания древостоя. В подмодели конкуренции необходимо предусмотреть возможность имитации конкуренции за другие (кроме азота) элементы почвенного питания и воду.
В текущей версии системы моделей используется статичный подход к генерации микрорельефа, выполняемый только на этапе инициализации. Необходим переход к динамической подмодели, двумя основными направлениями развития которой будут имитация изменений микрорельефа с течением времени и влияние микрорельефа на возобновление деревьев и растительности ТКЯ. Текущая версия подмодели распределения опада не учитывает неоднородность распределения биомассы внутри крон, а также влияние пространственной структуры древесного яруса и микрорельефа на распределение опада, следовательно, необходимо уточнение данных процедур.
Опыт, полученный при моделировании динамики древостоев на осушенных торфяниках (Shanin et al., 2021b), показал важность учёта уровня грунтовых вод и их влияния на продуктивность древесного яруса и успешность возобновления деревьев. Также необходимо внести изменения в подмодель динамики органического вещества почвы для имитации разложения части внутрипочвенного опада в анаэробных условиях.
В подмодели органического вещества почвы рассматривается динамика лабильных и стабильных пулов углерода, при этом углерод, находящийся в «сверхстабильном» состоянии, например органическое вещество глубоких почвенных горизонтов и пирогенный углерод (Lehmann, Kleber, 2015), в подмодели не учитывается, что может приводить к более выраженным, по сравнению с фактически наблюдаемыми, колебаниям в запасах ОрВП при смене растительных формаций (Luyssaert et al., 2008). Как следствие, необходимым дополнением в развитии подмодели, особенно важным при долгосрочном прогнозировании, является включение в подмодель соответствующего пула ОрВП. Ещё одним перспективным направлением развития подмодели является включение в систему моделей циклов других элементов (в первую очередь фосфора и кальция), используя уже существующие наработки (Хораськина и др., 2010; Komarov et al., 2012), а также моделирование динамики соответствующих элементов в древостое и элементах ТКЯ. Для более полного учёта взаимосвязей между разными компонентами лесных экосистем также предполагается включение в систему моделей блоков имитации ризосферного прайминг-эффекта (Припутина и др., 2021; Chertov et al., 2022) и микоризы. Очевидно также, что необходима отдельная подмодель, учитывающая связь между размерами КДО и скоростью их разложения, а также особенности конкретных фракций КДО (сухостой, валёж) (Didion et al., 2014; Shorohova, Kapitsa, 2014).
На данный момент видоспецифичные параметры были оценены только для 12 основных видов: Pinus sylvestris, Picea abies, Larix sibirica, Abies sibirica, Betula pendula / Betula pubescens (параметры для обоих видов приняты идентичными), Populus tremula, Quercus robur, Tilia cordata, Fagus sylvatica, Acer platanoides, Ulmus glabra, Fraxinus excelsior. Соответственно, ещё одним направлением работ является продолжение параметризации системы моделей (включая как оценку параметров для других видов деревьев, так и уточнение значений уже имеющихся параметров) для более точного моделирования динамики смешанных древостоев.
ИМИТАЦИОННЫЕ ЭКСПЕРИМЕНТЫ
Имитационные сценарии
Для проверки корректности работы системы моделей был сконструирован набор сценариев, имитирующих древостои с различным видовым составом, различной пространственной структурой и на разных стадиях развития. Имитационные эксперименты проводились на виртуальной площадке размером 100 × 100 м, разделённой на ячейки размером 0.5 × 0.5 м. Параметры имитационных сценариев приведены в таблице 6. Почвенно-климатические условия были приняты соответствующими ТЛУ С3 (Желдак, Атрохин, 2002) для подзоны хвойно-широколиственных лесов.
Таблица 6. Начальные параметры имитационных сценариев
| Код | Формула древостоя | Густота древостоя, шт. га−1 | Средняя высота, м | Средний диаметр ствола на уровне груди, см | Возраст, лет | Тип размещения деревьев в пространстве |
| 1. P_Yr | 10С | 4400 | 4.5 ± 0.2 | 6.0 ± 0.3 | 10 | ПС |
| 2. B_Yr | 10Б | 4400 | 4.5 ± 0.2 | 6.0 ± 0.3 | 10 | ПС |
| 3. P5B5_Yr | 5С5Б | 4400 | 4.5 ± 0.2 | 6.0 ± 0.3 | 10 | ПС |
| 4. P7B3_Yr | 7С3Б | 4400 | 4.5 ± 0.2 | 6.0 ± 0.3 | 10 | ПС |
| 5. P3B7_Yr | 7Б3С | 4400 | 4.5 ± 0.2 | 6.0 ± 0.3 | 10 | ПС |
| 6. P_Yc | 10С | 4400 | 4.5 ± 0.2 | 6.0 ± 0.3 | 10 | К |
| 7. B_Yc | 10Б | 4400 | 4.5 ± 0.2 | 6.0 ± 0.3 | 10 | К |
| 8. PB_Yc | 5С5Б | 4400 | 4.5 ± 0.2 | 6.0 ± 0.3 | 10 | К |
| 9. P_Yg | 10С | 4400 | 4.5 ± 0.2 | 6.0 ± 0.3 | 10 | Р |
| 10. B_Yg | 10Б | 4400 | 4.5 ± 0.2 | 6.0 ± 0.3 | 10 | Р |
| 11. PB_Yg | 5С5Б | 4400 | 4.5 ± 0.2 | 6.0 ± 0.3 | 10 | Р |
| 12. P_Mr | 10С | 400 | 27.7 ± 1.2 | 33.4 ± 2.3 | 100 | ПСР |
| 13. S_Mr | 10Е | 400 | 27.7 ± 1.2 | 33.4 ± 2.3 | 100 | ПСР |
| 14. B_Mr | 10Б | 400 | 27.7 ± 1.2 | 33.4 ± 2.3 | 100 | ПСР |
| 15. PS_Mr | 5С5Е | 400 | 27.7 ± 1.2 | 33.4 ± 2.3 | 100 | ПСР |
| 16. PB_Mr | 5Е5Б | 400 | 27.7 ± 1.2 | 33.4 ± 2.3 | 100 | ПСР |
| 17. L_Mr | 2Д2Лп2Кл2В2Я | 400 | 27.7 ± 1.2 | 33.4 ± 2.3 | 100 | ПСР |
| 18. PS_Tr | I: 10С | 400 | 27.7 ± 1.2 | 33.4 ± 2.3 | 100 | ПСР |
| II: 10Е | 1000 | 5.0 ± 0.5 | 10.0 ± 1.0 | 30 | ПС | |
| 19. BL_Tr | I: 10Б | 400 | 27.7 ± 1.2 | 33.4 ± 2.3 | 80 | ПСР |
| II: 2Д2Лп2Кл2В2Я | 1000 | 5.0 ± 0.5 | 10.0 ± 1.0 | 30 | ПС | |
| 20. PSL_Tr | I: 4С4Е2Б | 300 | 27.8 ± 2.9 | 40.7 ± 9.5 | 100 | ПСР |
| II: 5Е4Лп1Д | 700 | 12.3 ± 6.6 | 13.8 ± 2.8 | 30 | К | |
| 21. L_Tr | I: 2Д2Лп2Кл2В2Б | 300 | 28.0 ± 2.9 | 41.0 ± 9.6 | 50–150* | ПСР |
| II: 4В3Лп3Кл | 400 | 10.4 ± 1.3 | 15.1 ± 2.1 | 30 | ПС | |
| 22. S_Ur | 10Е | 700 | 2.0–33.0* | 2.4–55.8* | 10–200* | ПС |
Примечание: «I», «II» — показатели отдельно по ярусам древостоя. Для средней высоты и среднего диаметра ствола на уровне груди указаны среднее ± стандартное отклонение. Тип размещения деревьев в пространстве: «ПС» — псевдослучайное, «ПСР» — псевдослучайное с пороговым расстоянием (приоритет густоты древостоя); «К» — кластеризованное; «Р» — по регулярной схеме (4.5 м между рядами, 0.5 м между сеянцами в ряду). * — указан диапазон величины.
Результаты имитационных экспериментов анализировались по набору контрольных переменных, включая: (а) перехват ФАР на уровне отдельных деревьев (МДж на 1 кг абсолютно сухой биомассы листвы); (б) распределение подпологовой ФАР на уровне отдельных ячеек (в долях от надпологовой ФАР); (в) потребление азота в доступных для растений формах на уровне отдельных деревьев (в г на 1 кг абсолютно сухой биомассы тонких корней); (г) перекрывание корневых систем деревьев на уровне отдельных ячеек; (д) чистая первичная продукция древостоев за вегетационный сезон, кг га−1; (е) неоднородность пространственного распределения гидротермических характеристик почв. При анализе продуктивности древостоев одинаковой структуры, но с различным видовым составом также анализировался эффект «дополнительной продуктивности» (Loreau, 1998), основанный на расчёте отношения прогнозируемой продуктивности смешанного древостоя к его теоретической ожидаемой продуктивности. Последняя определяется как средневзвешенное значение величин прогнозируемой продуктивности соответствующих одновидовых древостоев, где мерой веса выступают доли видов в анализируемом смешанном древостое (Pretzsch et al., 2013). Таким образом, значения дополнительной продуктивности, превышающие 1, показывают влияние эффекта «разделения ниш» на рост продуктивности смешанных древостоев, по сравнению с одновидовыми. При анализе пространственной неоднородности гидротермических характеристик почв использовались данные метеорологической станции Коломна за 1976 год. Были выбраны 2 дня в весенний и летний периоды, для которых наиболее ярко проявляется влияние пространственной неоднородности на гидротермический режим. В 100‑й день года (09.04.1976 г.) снежный покров на открытом месте и под лиственными древостоями уже сошёл, под хвойными — ещё нет. Вегетация лиственных деревьев и растений живого напочвенного покрова ещё не началась. Среднесуточная температура воздуха составляет +4.5ºC. В 210‑й день (27.06.1976 г.) среднесуточная температура воздуха составляет 20.0ºC, суточное количество осадков — 10 мм. Предшествующая неделя была тёплой (среднесуточные температуры составляли 17.1–20.6ºC) и практически без осадков. Однако ранее в течение двух дней выпало 32 мм осадков, но за неделю тёплой и сухой погоды это количество воды должно было в значительной степени быть израсходованным на эвапотранспирацию.
Исходная метеорологическая информация, требуемая для подмодели гидротермического режима почвы (температура воздуха, атмосферные осадки и характеристики влажности воздуха (недостаток насыщения и относительная влажность суточного разрешения), была получена из массивов данных, подготовленных во Всероссийском НИИ гидрометеорологической информации — Мировом центре данных (ВНИИ ГМИ — МЦД) Росгидромета и доступных на сайте http://meteo.ru/data. Для характеристики климатических условий использовались данные метеорологической станции Коломна. В качестве базового периода для оценки статистических характеристик современного климата был выбран 30‑летний период 1981–2010 гг. Далее были сгенерированы стационарные климатические сценарии посредством выборки в случайном порядке данных за полные годы (с целью сохранения как внутригодичной автокорреляции параметров, так и корреляции между параметрами) до достижения 70‑летней продолжительности (с суточным шагом). Полученные сценарии были проверены на отсутствие трендов как путём визуального контроля диаграмм показателей, так и с помощью аппроксимации показателей линейной функциии (проверялось отсутствие значимых различий коэффициента наклона линейной функции от 0). Начальные запасы ОВ и азота в органическом и органоминеральном горизонтах почв в имитационных экспериментах были одинаковыми для всех ячеек имитируемого лесного участка; оценки запасов выполнены по данным полевых исследований почв авторами в ПТЗ. Пространственная дифференциация почвенных запасов ОВ и азота в имитационном эксперименте происходила за счёт поступления в ячейки модельной решётки разного количества видоспецифичных фракций растительного опада и зависимости интенсивности его трансформации (минерализации) от гидротермических условий соответствующих почвенных горизонтов. ТКЯ был представлен 5 видами: Calamagrostis arundinacea, Convallaria majalis, Pteridium aquilinum, Vaccinium myrtillus и Vaccinium vitis‑idaea. Моделировались 3 сценария развития древостоя. Первый сценарий — полидоминантный древостой из Pinus sylvestris, Picea abies, Betula spp. и Populus tremula с псевдослучайным расположением деревьев. Начальные запасы С и N в органическом горизонте: C — 2.625 кг м−2, N — 0.054 кг м−2, в органоминеральных — 3.14 и 0.19 кг м−2, соответственно. Второй сценарий — сосново-берёзовый древостой с расположением деревьев несколькими плотными кластерами. Начальные запасы С и N в почве — аналогично предыдущему сценарию. Третий сценарий — культуры Pinus sylvestris с расположением деревьев по регулярной квадратной решётке с шагом 2 × 2 м. Предполагалось, что в результате формирования посадочных борозд органогенный горизонт почв сильно нарушен, а начальные запасы С и N соответствуют запасам в органоминеральной части профиля: C — 1.393 кг м−2, N — 0.103 кг м−2.
Помимо сценариев развития лесных экосистем без нарушений, имитировалось влияние внешних факторов воздействия: выборочных рубок с изъятием 30% наиболее крупных деревьев (по сумме площадей сечений), изменений климата (по сценариям RCP 4.5, RCP 6.0 и RCP 8.5 из 5‑го оценочного доклада МГЭИК (IPCC, 2013)) и 50% роста поступления соединений азота с атмосферными осадками, по сравнению с базовым уровнем (Jia et al., 2016).
Результаты и обсуждение
Для компактного представления пространственно распределённых показателей (на уровне отдельных деревьев или ячеек имитационной решётки) в единичный момент времени используется вариограмма, которая изображает распределения анализируемых показателей для нескольких имитационных сценариев с использованием кривых плотности вероятности. Ширина каждой кривой соответствует приблизительной частоте точек данных с соответствующим значением показателя на оси ординат. Горизонтальные линии на вариограмме соответствуют медианным значениям соответствующих показателей. Для представления динамики пространственного распределения показателей на уровне ячеек имитационной решетки используется диаграмма, представляющая собой вертикальную последовательность распределений плотности вероятности анализируемого показателя для различных шагов моделирования, выровненную по горизонтальному масштабу. Все представленные результаты следует рассматривать как предварительные, поскольку на данном этапе основной целью имитационных экспериментов являлось тестирование функциональных возможностей системы моделей по воспроизведению функциональных взаимосвязей между разными компонентами лесных экосистем с учётом влияния пространственной неоднородности на разных уровнях, а не демонстрация применения системы моделей для решения конкретных практических или исследовательских задач. В связи с этим временная динамика продемонстрирована только для тех показателей, на которые влияние пространственной неоднородности носит кумулятивный характер.
Конкуренция за ресурсы и продукционные показатели древостоев
Анализ результатов имитационных экспериментов позволил выявить ряд аспектов в функционировании моделируемых лесных экосистем. Показано, что интенсивность корневой конкуренции в древостое в большей степени зависит от его видового состава и пространственной структуры, чем от возраста, хотя наблюдается некоторое увеличение интенсивности конкуренции за элементы почвенного питания в спелых древостоях, по сравнению с молодняками (рис. 15). Одновременно, по мере увеличения возраста древостоя, в нём возрастает однородность в пространственном распределении плотности конкуренции. Это объясняется тем, что кратность перекрытия корневых систем значительно превышает кратность перекрытия проекций крон, что было показано ранее (Санников, Санникова, 2014). Подобная плотность перекрытия корневых систем связана, в первую очередь, с высокой дальностью горизонтального распространения корней относительно размеров кроны и, как следствие, с намного более высокой площадью корневой системы дерева, по сравнению с площадью проекции его кроны.
Рисунок 15. Распределение интенсивности корневой конкуренции (количество перекрытий зон питания на 1 м2 имитационной решётки) в древостоях разного состава и пространственной структуры. Коды и характеристики сценариев приведены в таблице 6. Горизонтальными линиями показаны медианные значения
Различия в начальном расположении деревьев также оказывают влияние на характер корневой конкуренции. При псевдослучайном начальном расположении деревьев распределение перекрытий зон питания близко к нормальному. При кластеризованном расположении деревьев данное распределение бимодально, с одним пиком (в области высокой интенсивности конкуренции), соответствующим группам деревьев с плотным расположением, и вторым пиком в области промежутков между такими кластерами, где интенсивность конкуренции невысока. При расположении деревьев по регулярной решётке наблюдается несколько пиков, связанных с более высокой плотностью перекрытия зон питания в пределах рядов и менее высокой — в междурядьях. В спелых древостоях с одним ярусом плотность пересечения зон питания ниже, чем в древостоях с более сложной структурой древесного яруса (рис. 15).
Рисунок 16. Совокупное годичное потребление азота на уровне отдельных деревьев, кг на 1 кг биомассы тонких корней в древостоях разного состава и пространственной структуры
Согласно модельным оценкам, потребление азота деревьями снижается с увеличением их возраста: от порядка 0.010 кг азота на 1 кг биомассы тонких корней в год в молодняках до 0.002–0.005 — в спелых древостоях. Разновозрастные и смешанные древостои демонстрируют более эффективное потребление ресурсов (за счёт более равномерного распределения биомассы подземных органов), по сравнению с одновозрастными одновидовыми древостоями. Пространственная структура не оказывает существенного влияния на медианное значение данного показателя, но влияет на характер его распределения (рис. 16). Пониженные значения потребления азота в разновозрастных древостоях, помимо заложенного в системе моделей снижения эффективности потребления азота по мере старения деревьев, могут объясняться более сильным конкурентным давлением со стороны крупных деревьев. На величину потребления азота в ельниках также дополнительно влияет более высокая, по сравнению с другими древостоями, насыщенность почвы корнями, что может быть объяснено более высокой долей биомассы тонких корней (от общей массы дерева) у Picea abies, по сравнению с деревьями других видов (Helmisaari et al., 2002). Также в большинстве смешанных древостоев величина потребления азота оказалась выше, чем ожидаемая, которая может быть рассчитана как среднее арифметическое между интенсивностью потребления в чистых древостоях, сформированных видами, входящими в данный смешанный древостой. Это, на наш взгляд, подтверждает эффективную реализацию заложенных в системе моделей механизмов имитации «разделения ниш», которые состоят, в частности, в том, что надземные и подземные органы деревьев разных видов отличаются характером вертикального распределения, снижая тем самым интенсивность конкуренции и повышая эффективность использования ресурсов (Cavard et al., 2011; Pretzsch et al., 2015).
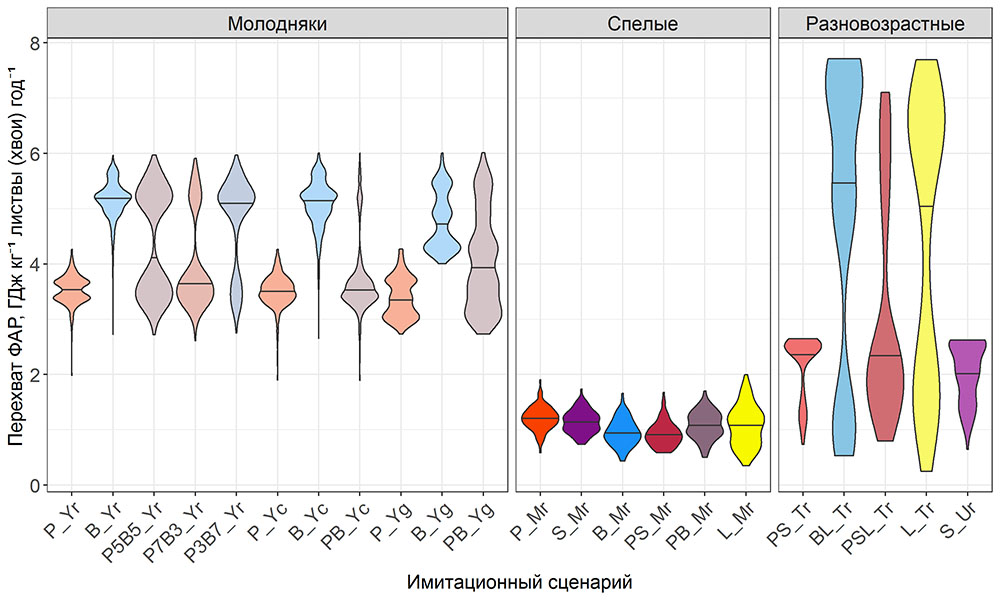
Рисунок 17. Перехват ФАР на уровне отдельных деревьев (ГДж на 1 кг листвы/хвои, сумма за вегетационный сезон) в древостоях разного состава и пространственной структуры
В целом, имитационные эксперименты показали более высокий показатель перехвата ФАР лиственными деревьями (на 1 кг биомассы листвы), по сравнению с хвойными. Значения данного показателя выше для стадии молодняков, что мы связываем с более разреженным размещением деревьев и меньшим, по сравнению со спелыми и разновозрастными древостоями, затенением листвы (хвои) в нижних слоях полога. Размещение деревьев по регулярной решётке повлияло на иной характер распределения и медианное значение перехвата ФАР в молодняках, в сравнении с псевдослучайным и кластеризованным размещением. Основное влияние здесь оказывает взаимное затенение деревьев в пределах ряда, которое не может быть полностью компенсировано разрастанием крон в направлении междурядий (рис. 17). Медианное значение перехвата ФАР в разновозрастных древостоях выше, по сравнению со спелыми.
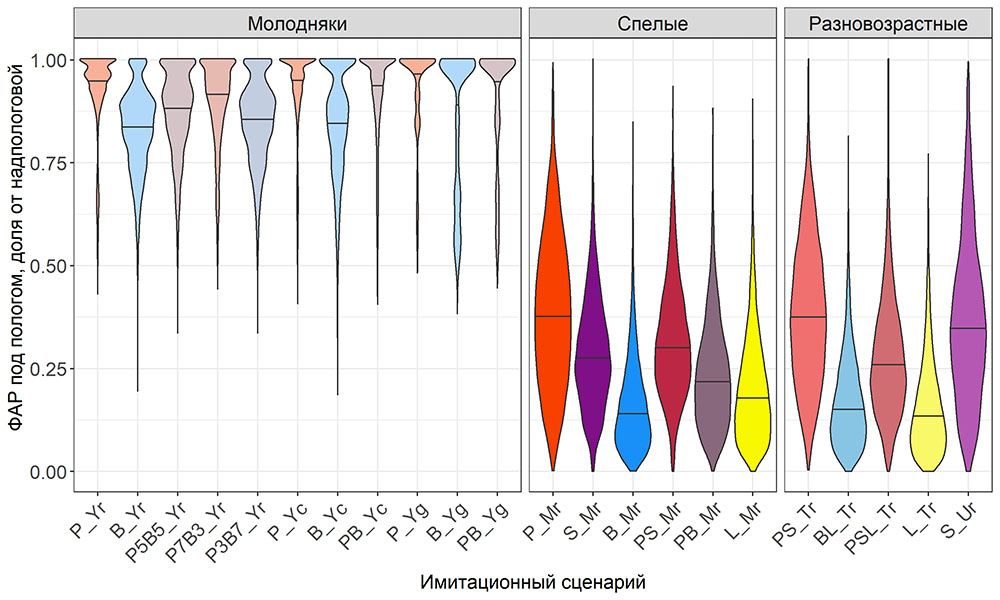
Рисунок 18. Распределение ФАР, приходящей на поверхность почвы (доля от надпологовой) на уровне отдельных ячеек имитационной решётки в древостоях разного состава и пространственной структуры
Таким образом, при кластеризованном размещении освоение ресурсов как на уровне отдельных деревьев, так и на уровне древостоя в целом является менее эффективным, т. к., с одной стороны, конкуренция в плотных группах очень высока, что лимитирует количество ресурсов на уровне отдельного дерева, а с другой стороны, возможность прорастания в «окна» корневых систем и в особенности крон деревьев ограничена. Размещение деревьев по регулярной решётке в ряде случаев оказалось даже эффективнее псевдослучайного в отношении использования ресурсов, однако следует учитывать особенности данных древостоев, связанные с их более низкой устойчивостью. При развитии древостоев с подобной структурой интенсивность конкуренции имеет схожие показатели для всех деревьев, что может приводить на определённом этапе к их взаимному угнетению и последующему интенсивному самоизреживанию (Припутина и др., 2016), а гибель части деревьев в древостоях такой структуры создаёт большие разрывы в пологе, которые не могут быть компенсированы боковым разрастанием крон ближайших деревьев. В то же время, в древостоях с псевдослучайным расположением деревьев (даже одновидовых и одновозрастных), ряд деревьев имеет преимущество в силу более низкого конкурентного давления на них со стороны соседних деревьев, что на уровне древостоя может способствовать более эффективному потреблению ресурсов, а также повышает устойчивость таких древостоев к самоизреживанию.
Анализ распределения ФАР под пологом ожидаемо показал, что в молодняках отсутствуют сильно затенённые участки. В хвойных древостоях доля хорошо освещённых участков выше, что объясняется более компактными кронами, которые (при одинаковых плотности древостоя и размерах деревьев, принятых во всех имитационных сценариях) дают больше «разрывов» в пологе. В спелых хвойных древостоях распределение ФАР под пологом более равномерное, по сравнению со спелыми древостоями лиственных видов (рис. 18). В спелых лиственных древостоях доля сильно затенённых ячеек выше.
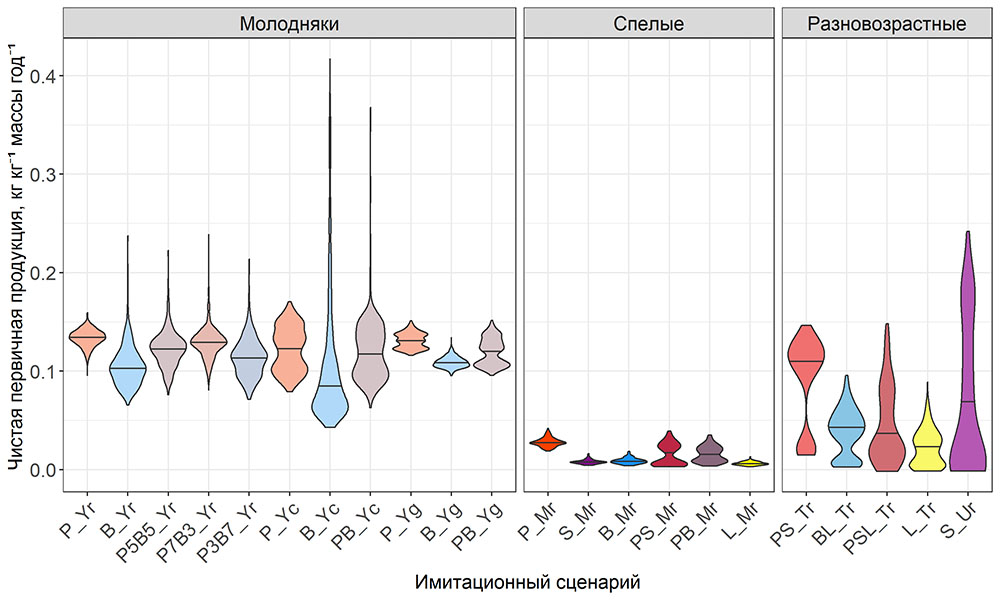
Рисунок 19. Продуктивность на уровне отдельных деревьев (кг чистой первичной продукции в год на 1 кг общей биомассы дерева) в древостоях разного состава и пространственной структуры
Величина чистой первичной продукции (в кг на 1 кг общей биомассы дерева) ожидаемо выше в молодняках. Пиковые значения продуктивности в молодняках с кластеризованным размещением соответствуют отдельным деревьям, растущим в разреженных участках древостоев, которые, как следствие, практически не лимитированы доступной ФАР и менее лимитированы количеством доступного азота. Также высокие значения продуктивности наблюдаются в древостоях со сложной структурой, особенно в абсолютно разновозрастном ельнике (рис. 19). Величины дополнительной продуктивности для смешанных молодняков составляют: 1.028 для 7С3Б, 1.036 для 5С5Б, и 1.030 — для 3С7Б.
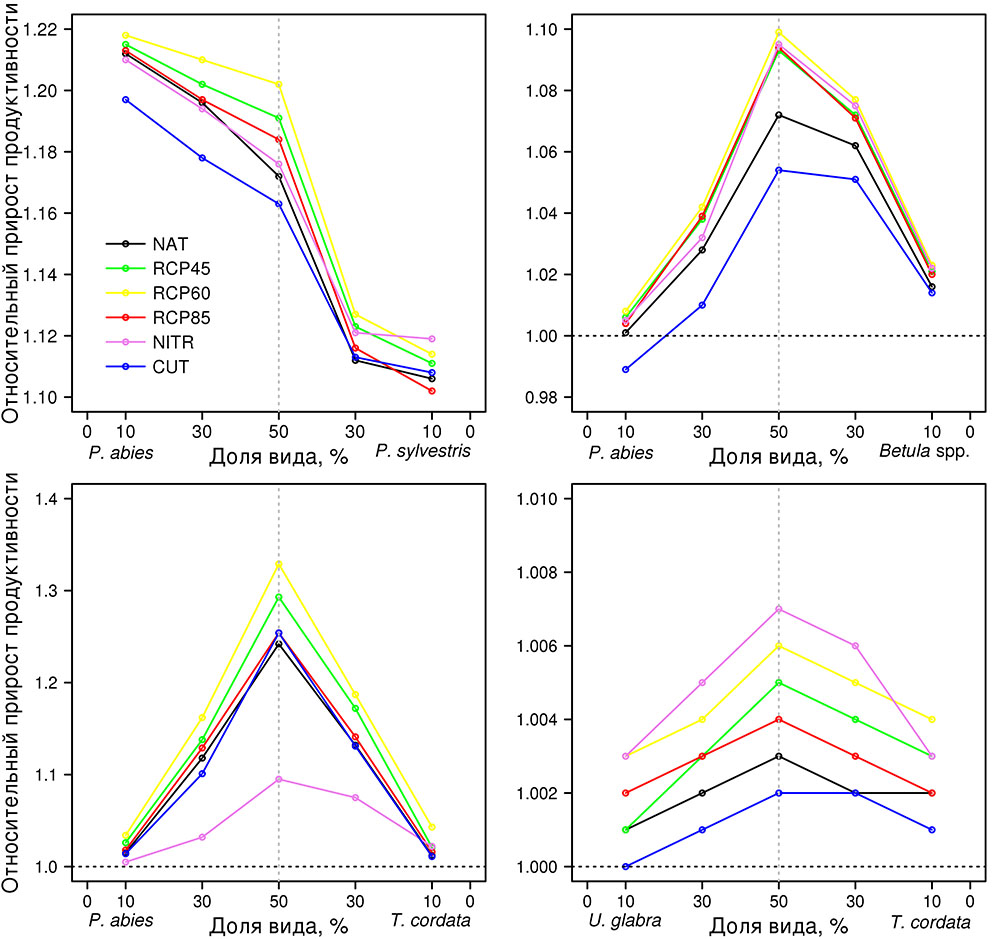
Рисунок 20. Прогнозируемые значения дополнительной продуктивности в смешанных древостоях разного состава при сценарии без рубок (NAT), изменениях климата (RCP45, RCP60 и RCP85), росте поступления соединений азота с атмосферными осадками (NITR) и выборочных рубках (CUT)
Практически во всех смоделированных вариантах смешанных древостоев значение дополнительной продуктивности было выше 1 (рис. 20). Значения дополнительной продуктивности в большинстве сценариев воздействий были выше, чем в сценарии без нарушений, что показывает более высокую устойчивость смешанных древостоев к внешним воздействиям. Также показатель дополнительной продуктивности выше в древостоях, сформированных видами с различающимися эколого-ценотическими стратегиями.
Неоднородность гидротермических условий и динамики органического вещества почвы
Анализ результатов имитационных экспериментов по оценке пространственного варьирования гидротермических характеристик почвы показал, что в 100‑й день года влажность почвы во всех лиственных древостоях остаётся однородной в пространственном отношении. При этом в подстилке, где среднее значение влажности почвы составляет 0.17 м3 м−3 (рис. 21), влажность снизилась в сравнении с заданным на начало имитационного эксперимента значением 0.30 м3 м−3, а в нижележащем органоминеральном горизонте возросла — до 0.24 м3 м−3 (рис. 22) в сравнении с начальным — 0.20 м3 м−3.
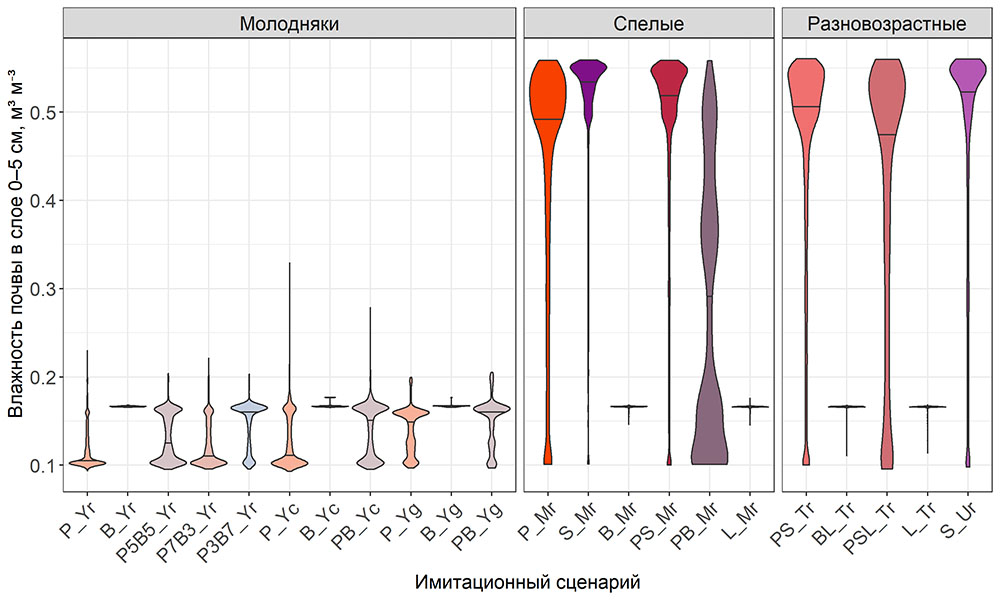
Рисунок 21. Распределение влажности в слое 0–5 см в 100‑й день года под древостоями разного состава и пространственной структуры
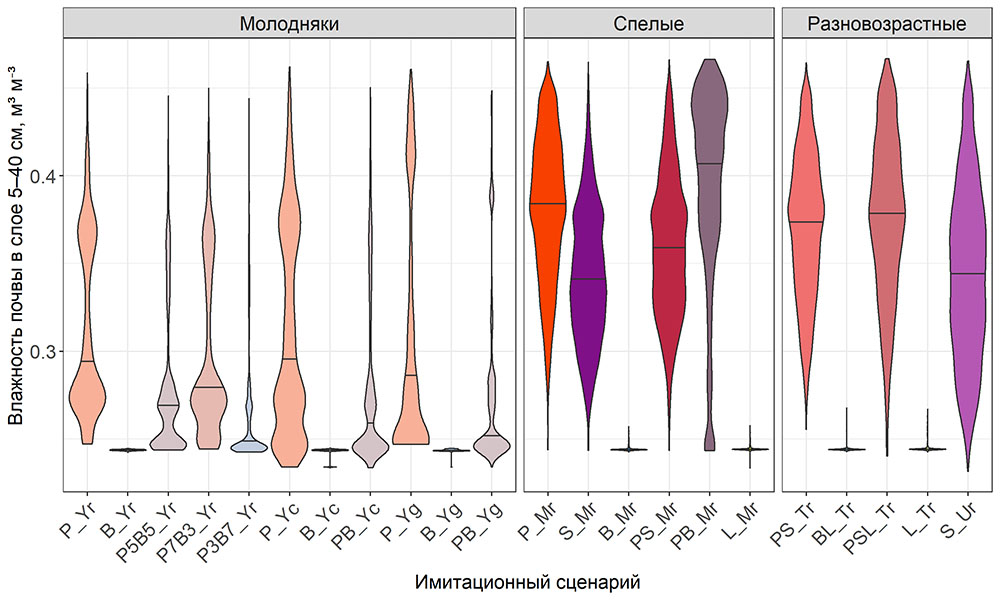
Рисунок 22. Распределение влажности почвы в слое 5–40 см в 100‑й день года под древостоями разного состава и пространственной структуры
В смешанных молодняках с участием Pinus sylvestris и Betula spp. распределение влажности подстилки бимодально, с модами, одно из значений которых аналогично значению под рассмотренными выше лиственными древостоями (0.17 м3 м−3), и другое соответствует наименьшей влагоёмкости (0.10 м3 м−3). Влажность органоминерального горизонта в этом варианте древостоев варьирует в диапазоне от значений, близких к соответствующей данному горизонту наименьшей влагоёмкости (0.25 м3 м−3) до значений 0.45 м3 м−3, что близко к показателю полной влагоёмкости (0.49 м3 м−3); при этом пространственно преобладают низкие значения. По-видимому, редко встречающиеся ячейки с высокими значениями влажности органоминерального горизонта соответствуют областям более сильного затенения, где снег сошёл позже и не вся избыточная влага успела просочиться в нижележащие горизонты. Подтверждением этому можно считать картину в спелых и разновозрастных хвойных древостоях, где, очевидно, таяние снежного покрова, вследствие более значительного затенения, ещё не закончилось. Соответственно, распределение влажности в подстилке асимметрично с модой в области высоких значений, тогда как в органоминеральном горизонте оно ближе к симметричному, т. е. на части имитационной площадки влажность уже успела значительно повыситься, на части — ещё нет, но преобладают промежуточные значения. Пространственная неоднородность темпов снеготаяния создаёт предпосылки к формированию локусов эфемероидных растений, активно участвующих в биологическом круговороте элементов.
Температура подстилки в 100‑й день под всеми лиственными древостоями составляет около +3.8 °C (что на 0.7 °C ниже температуры воздуха), а в почве на глубине 20 см — около +2.3 °C с относительно равномерным распределением в пространстве вследствие более дружного схода снежного покрова в условиях слабого затенения. Под молодняками с участием Pinus sylvestris значения температуры в среднем практически такие же с несколько большей дисперсией и отдельными незначительными выбросами в сторону пониженных температур, очевидно, в местах более позднего схода снега. В спелых и разновозрастных древостоях с участием хвойных пород диапазон температур существенно шире (+0.3 … +3.9 °C в подстилке и +0.3 … +2.4 °C на глубине 20 см), при этом распределение бимодальное с модами, близкими к краям диапазона и низкой повторяемостью промежуточных значений (рис. 23, 24). Такая пространственная неоднородность, очевидно, обусловлена неодновременным сходом снежного покрова, в более затененных местах ещё не завершившимся.
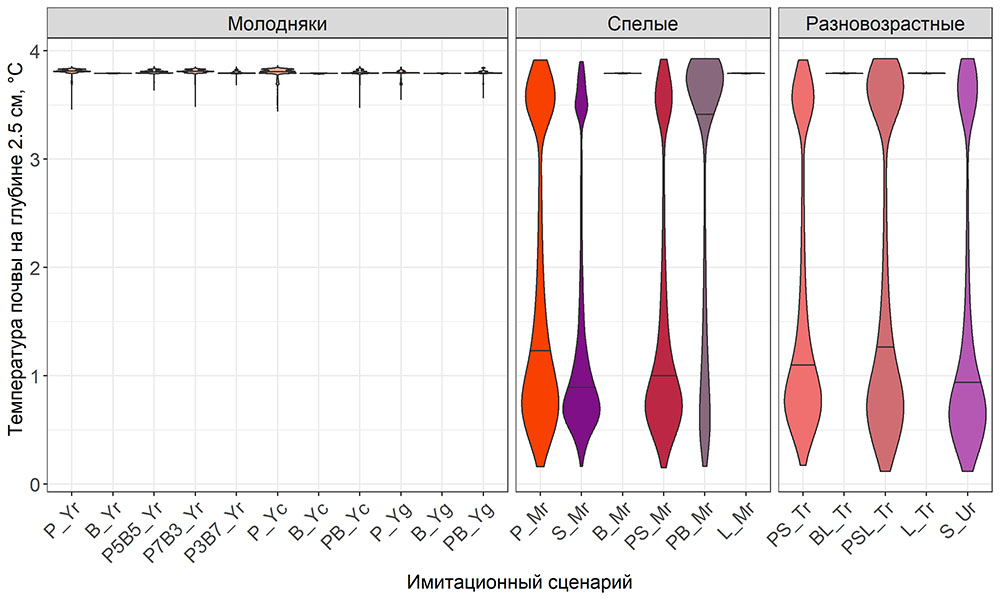
Рисунок 23. Распределение температуры на глубине 2.5 см в 100‑й день года под древостоями разного состава и пространственной структуры
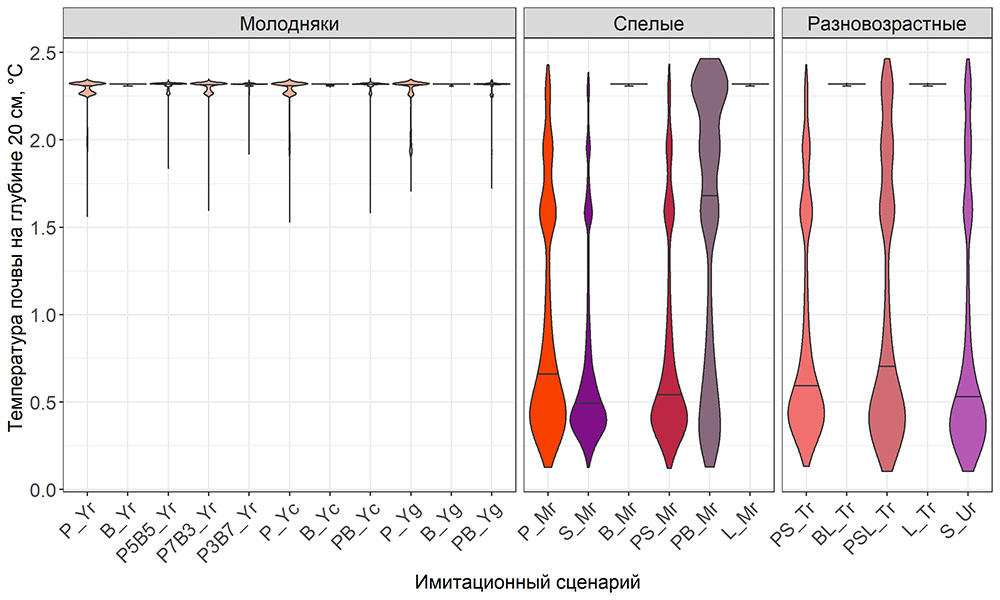
Рисунок 24. Распределение температуры почвы на глубине 20 см в 100‑й день года под древостоями разного состава и пространственной структуры
В 210‑й день под молодняками распределение влажности подстилки отчётливо выраженное бимодальное с максимальной повторяемостью значений 0.31 и 0.20–0.23 м3 м−3. В спелых и разновозрастных древостоях значения влажности подстилки (рис. 25) в основном сосредоточены в диапазоне 0.14–0.24 м3 м−3, крайне редко достигая максимальных значений, близких к таковым в молодняках. В органоминеральном горизонте (рис. 26) молодняков — асимметричное распределение с повышенной повторяемостью относительно высоких значений (около 0.30–0.33 м3 м−3 с максимальными значениями до 0.35 м3 м−3 и относительно редкими отклонениями в сторону пониженных значений (0.18–0.30 м3 м−3). Под спелыми и разновозрастными древостоями распределения значений влажности органоминерального горизонта более разнообразны. В ельниках пространственно преобладают более высокие значения влажности при относительно узком диапазоне значений, в березняках и сосняках — более низкие, при более широком диапазоне. В широколиственных древостоях наблюдается максимально широкий диапазон с преобладанием более высоких значений.
Мы предполагаем, что выпавшие в этот день 10 мм осадков (после недели без осадков и при повышенной относительно нормы температуре) заметно проявили себя только в молодняках, тогда как на влажности подстилки и тем более органоминерального горизонта почв в спелых и разновозрастных древостоях они сказались сравнительно слабо вследствие повышенной транспирации.
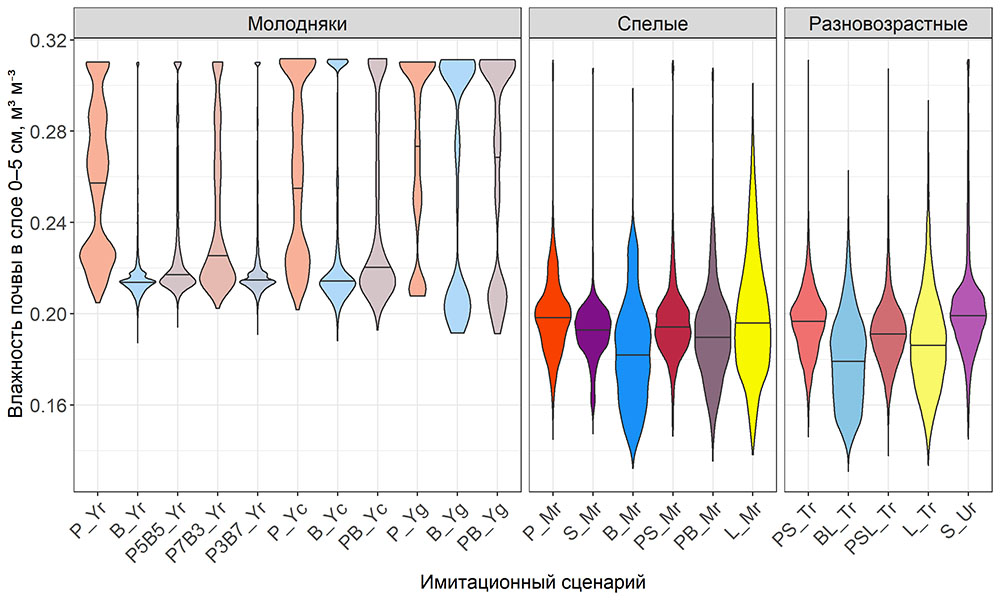
Рисунок 25. Распределение влажности в слое 0–5 см в 210‑й день года под древостоями разного состава и пространственной структуры
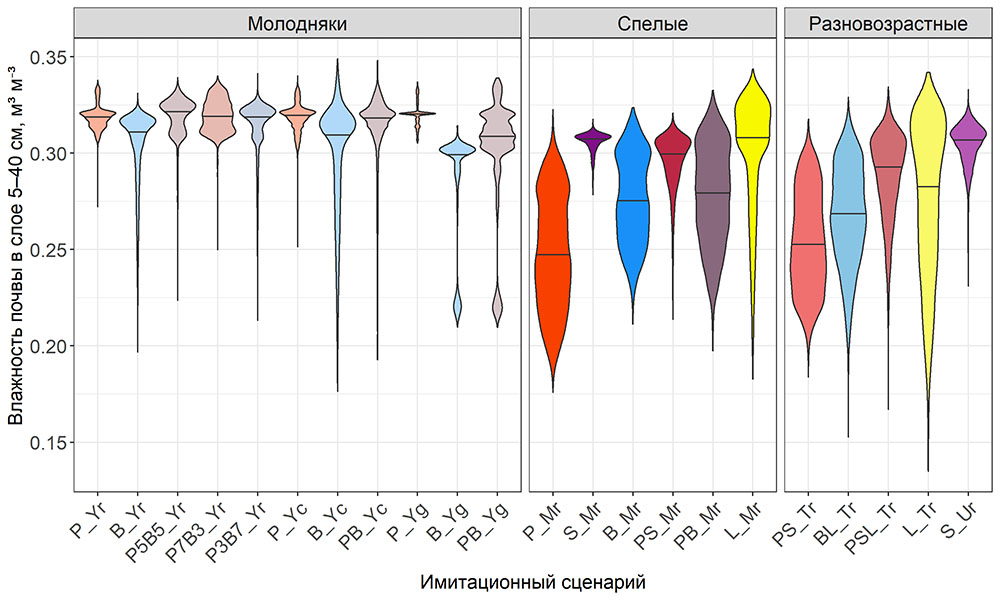
Рисунок 26. Распределение влажности в слое 5–40 см в 210‑й день года под древостоями разного состава и пространственной структуры
Согласно расчётам, температура подстилки в 210‑й день (рис. 27) на 2.0–2.5 ºC, а органоминерального горизонта — на 7.0–7.5 ºC ниже температуры воздуха (рис. 28). Пространственная неоднородность поля температур в молодняках менее выражена, чем под спелыми и разновозрастными древостоями.
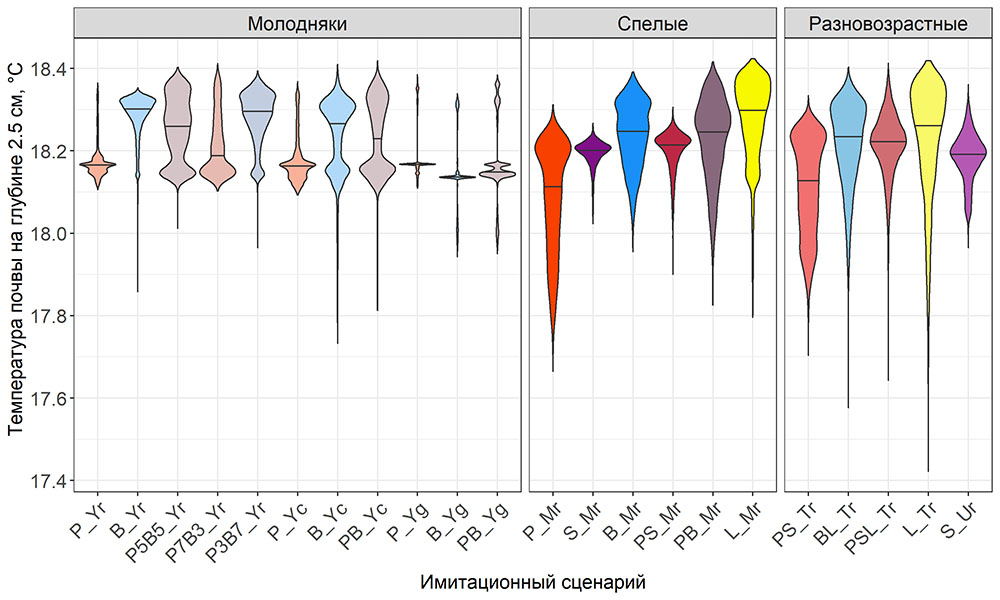
Рисунок 27. Распределение температуры почвы на глубине 2.5 см в 210‑й день года под древостоями разного состава и пространственной структуры
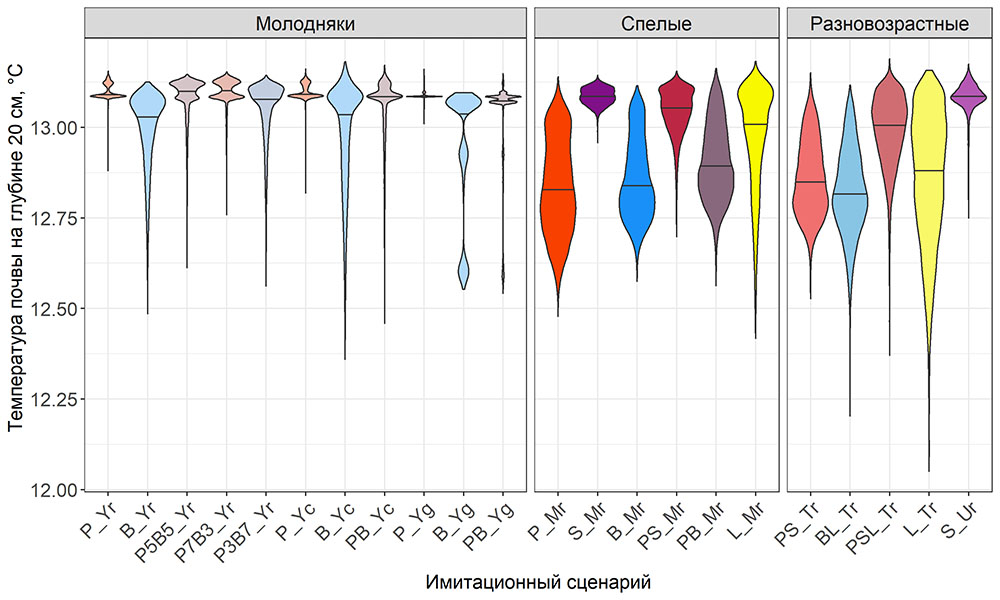
Рисунок 28. Распределение температуры почвы на глубине 20 см в 210‑й день года под древостоями разного состава и пространственной структуры
Анализ результатов имитационных экспериментов по оценке пространственного варьирования запасов органического вещества (С) и азота (N) в почвенном покрове лесных фитоценозов основан на сравнении данных трёх сценариев развития древостоев от молодняков (5–10 лет) до приспевающих (70 лет), в каждом из которых были рассмотрены два варианта поступления растительных опадов: (1) пространственно-локализованный в соответствии со структурой древостоя видоспецифичный опад только древесного яруса и (2) опад древостоя совместно с опадом растений травяно-кустарничкового яруса.
В сценарии полидоминантного древостоя из Pinus sylvestris, Picea abies, Betula spp. и Populus tremula с псевдослучайным расположением деревьев почвенно-растительные условия имитируемого участка приближены к условиям ППП в Приокско-Террасном заповеднике, где проводились полевые исследования. Визуализация результатов расчётов показывает схожий с полевыми данными характер распределения запасов С и N в почвенных горизонтах. В прогнозных расчётах, начиная с первых шагов моделирования, воспроизводится пространственная неоднородность распределения пулов C и N между подкроновыми и межкроновыми участками за счёт разницы в количестве поступающего поверхностного опада. Учёт в имитационных оценках дополнительно опада травяно-кустарничкового яруса создаёт бóльшую пространственную неоднородность почвенных показателей в молодых и средневозрастных древостоях с менее сомкнутым пологом крон, что нашло отражение на диаграммах распределения вероятности значений запасов углерода и азота (рис. 29). К возрасту древостоя 70 лет распределение запасов ОВ и азота в лесной подстилке определяется преимущественно характером поступления опада древесного яруса, а влияние растений травяно-кустарничкового яруса минимально, о чём свидетельствуют схожие диаграммы распределения запасов для рассматриваемых сценариев. Для органоминеральных горизонтов модельные расчеты в обоих вариантах опадов показывают бóльшую неоднородность пространственного распределения запасов С и N по сравнению с подстилкой, что согласуется с данными полевых исследований (Priputina et al., 2020).
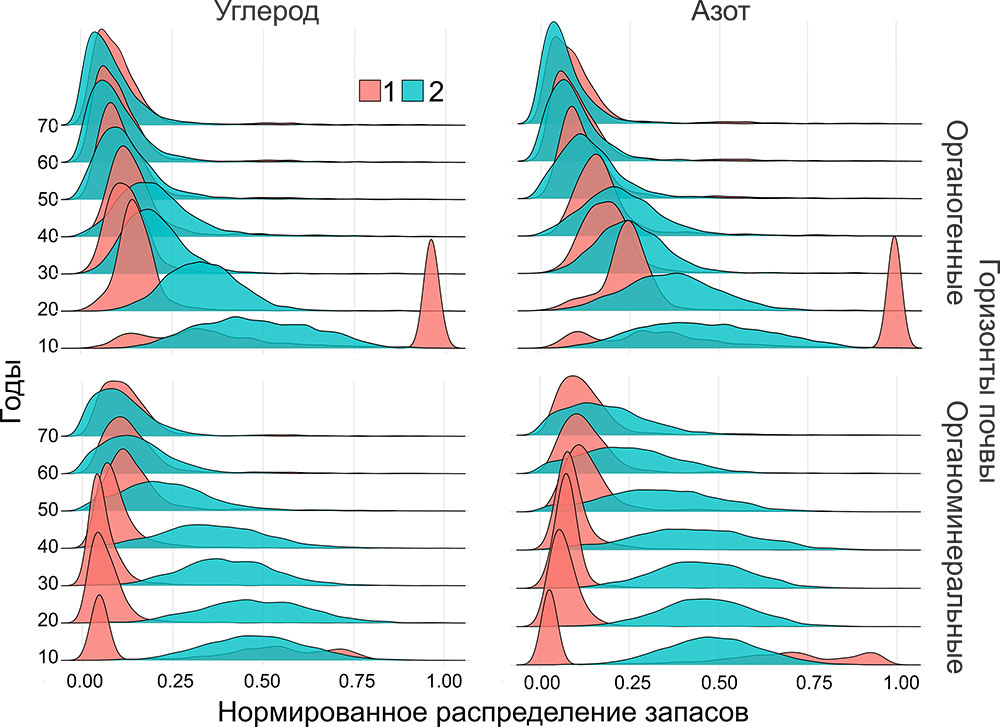
Рисунок 29. Нормированное распределение запасов органического вещества в пересчёте на углерод (С) и азота (N) в органогенных (лесная подстилка) и органоминеральных горизонтах почв в сценарии полидоминантного древостоя с псевдослучайным расположением деревьев. 1 — в модельных расчётах учитывался только опад древостоя, 2 — с учётом опада древостоя и травяно-кустарничкового яруса. По оси Х показано нормированное распределение запасов в градации от минимального до максимального на участке на соответствующем временном шаге
Более наглядно вклад растений травяно-кустарничкового яруса в поддержание запасов почвенного органического вещества демонстрируют данные динамики усреднённых показателей запасов С и N, рассчитанных как среднее для всего имитируемого участка (рис. 30). Как можно видеть на приведённых диаграммах, при учёте опада растений травяно-кустарничкового яруса система моделей показывает повышенные запасы С и N в органических горизонтах (лесной подстилке) по сравнению с вариантом поступления опада только от древостоя. Это объясняется в том числе тем, что подмодель динамики органического вещества почвы учитывает поступление части корневого опада кустарничков и трав в лесную подстилку. В органоминеральных горизонтах вклад растений напочвенного покрова в динамику запасов органического вещества менее выражен.
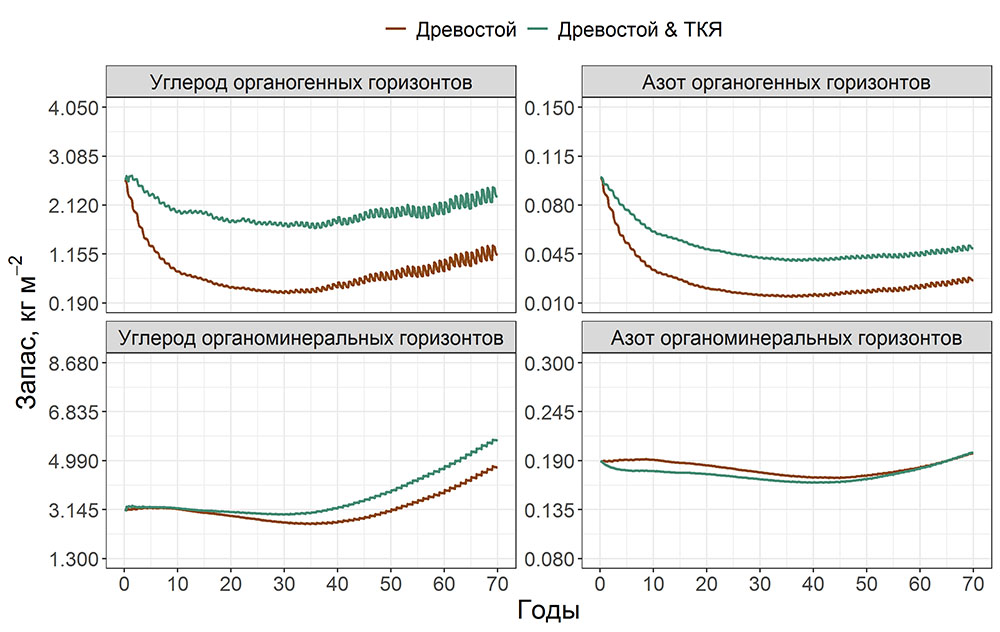
Рисунок 30. Динамика распределения запасов углерода и азота в лесной подстилке (органогенные горизонты) и органоминеральной части профиля в сценарии полидоминантного древостоя с псевдослучайным расположением деревьев: средние значения показателей для соответствующих почвенных горизонтов
В сценарии с кластеризованным размещением видов деревьев со схожей эколого-ценотической стратегией (Pinus sylvestris и Betula spp.) прослеживается значимая роль конкуренции за ресурсы между близко растущими деревьями как фактора снижения продукции листвы/хвои, что находит отражение в пониженных запасах С и N для участков внутри кластеров, которые сформированы деревьями одного вида. В отличие от полидоминантного древостоя с псевдослучайным размещением, кластерная структура размещения деревьев разных видов, опад которых различается по содержанию азота, формирует более контрастное распределение в пространстве биогеоценоза почвенных запасов С и N, особенно на стадии молодняков, о чём свидетельствует наличие 2–3 пиков нормированного распределения в сценарии без учёта опада травяно-кустарничкового яруса (рис. 31). При учёте вклада растений напочвенного покрова в суммарный пул растительного опада контрастность распределения показателей в пространстве несколько снижается. Одновременно с этим, как и в сценарии полидоминантного древостоя, наблюдаются заметные различия в характере распределения почвенных запасов С и N для органогенных и органоминеральных горизонтов. Динамика средних для имитируемого участка показателей запасов C и N в целом аналогична предыдущему сценарию (рис. 32), но для запасов С в лесной подстилке на стадии приспевающих древостоев различия между вариантами опадов менее выражены. Это может объясняться как различиями в качестве опадов сосново-берёзового и полидоминантного древостоев, так и заметным снижением вклада опада травяно-кустарничкового яруса в суммарный опад из-за затенения под пологом приспевающих древостоев.
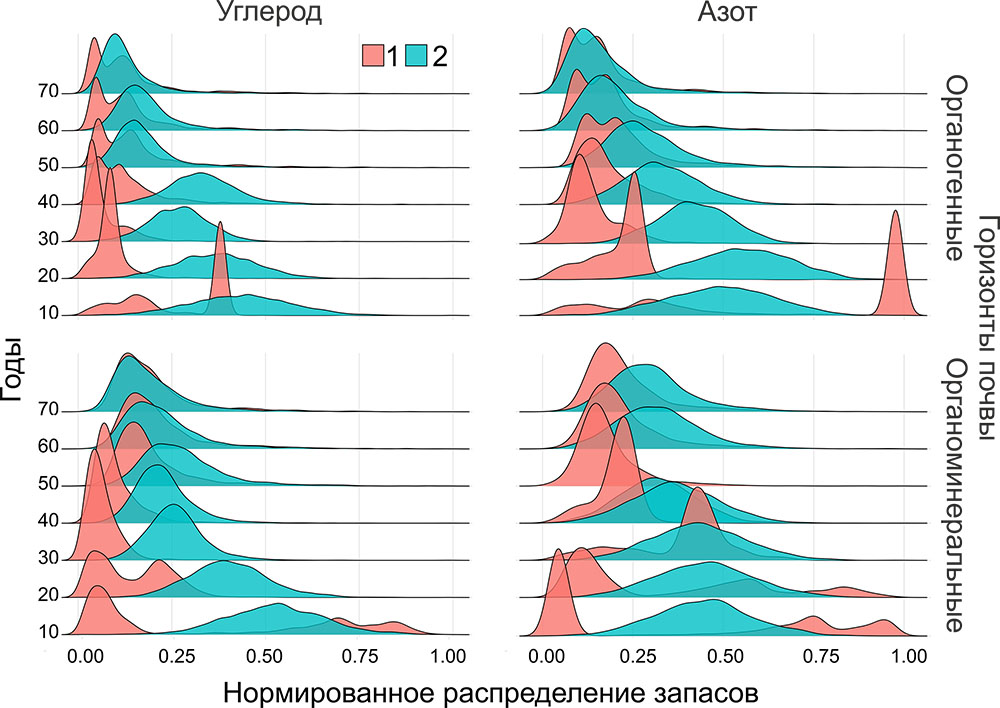
Рисунок 31. Нормированное распределение запасов С и N в органогенных (лесная подстилка) и органоминеральных горизонтах почв в сценарии сосново-берёзового древостоя с кластеризованным размещением деревьев. Условные обозначения — аналогично рис. 29
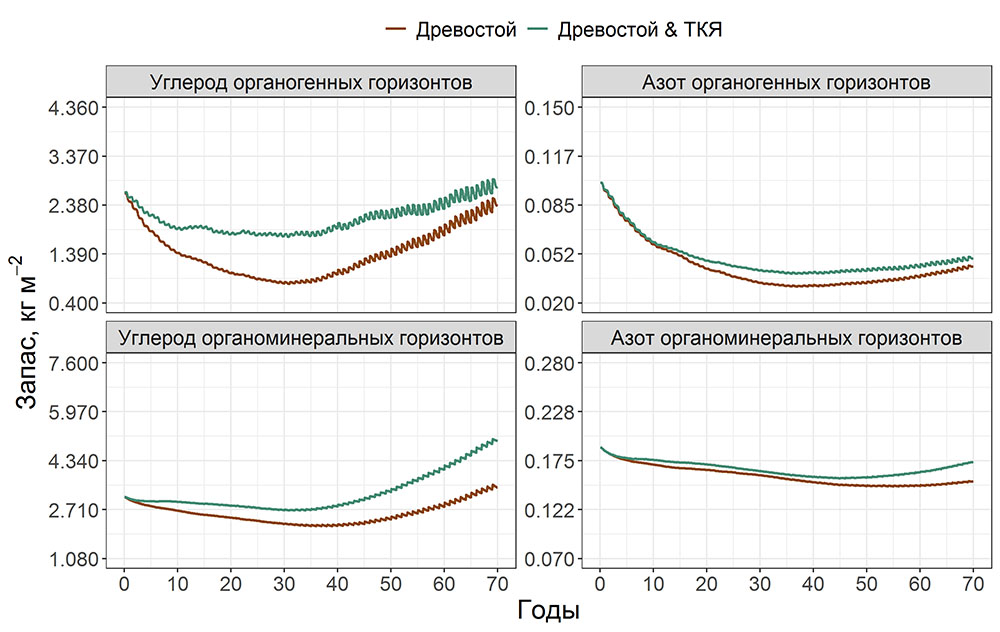
Рисунок 32. Динамика распределения запасов С и N в лесной подстилке (органогенные горизонты) и органоминеральной части почвенного профиля в сценарии сосново-берёзового древостоя с кластеризованным размещением деревьев: средние значения показателей для соответствующих горизонтов
В сценарии создания культур Pinus sylvestris с размещением деревьев по регулярной решётке результаты прогнозных оценок отражают важную роль растений напочвенного покрова в поддержании почвенного плодородия на начальных этапах роста лесных культур, когда масса ежегодного опада, формируемого древостоем, невелика, а его пространственное распределение на поверхности и в корнеобитаемом слое почв сильно локализовано (рис. 33). Заметные различия между распределением показателей в органогенных и органоминеральных горизонтах объясняются тем, что по сценарию культуры Pinus sylvestris сформированы на почве с отсутствующей лесной подстилкой. Диаграммы отражают особенности накопления и распределения запасов С и N при её формировании, а показываемое системой моделей наличие двухвершинного распределения запасов в возрасте спелых древостоев в случае учёта только опада древесного яруса соответствует различиям между подкроновыми и межкроновыми участками.
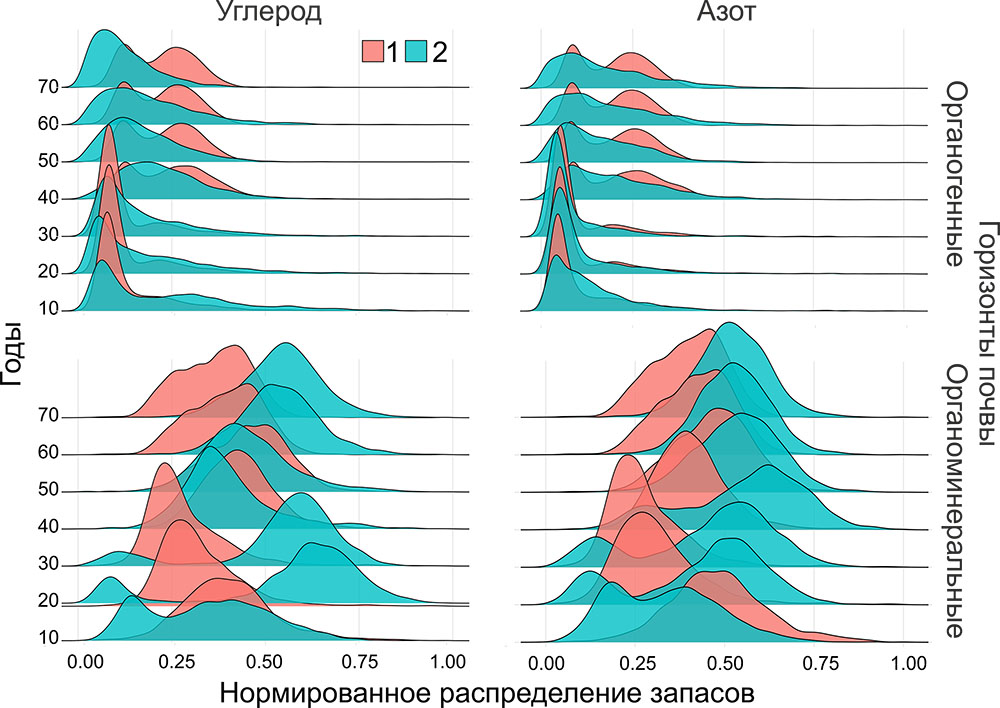
Рисунок 33. Нормированное распределение запасов С и N в органогенных (лесная подстилка) и органоминеральных горизонтах почв в сценарии сосновых культур с регулярной схемой посадки. Условные обозначения — аналогично рис. 29
Эти различия особенно заметны при анализе средних показателей динамики ОВ в лесной подстилке (рис. 34), которая в данном сценарии формируется заново после нарушений, связанных с подготовкой участка к посадке лесных культур. В реальных условиях создания лесных культур такой контрастности почвенных условий не наблюдается, что объясняется ролью опада растений напочвенного покрова, активно развивающегося в условиях отсутствия конкуренции со стороны древостоя и более богатого азотом, чем фракции соснового опада. Все это способствует формированию менее контрастной картины пространственного распределения запасов органического вещества и азота в почвах.
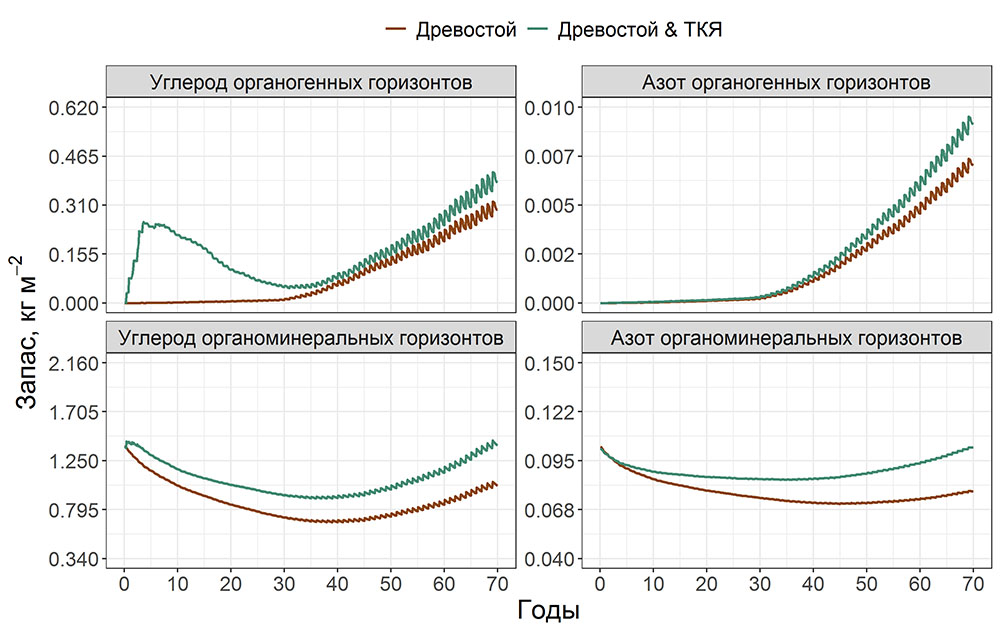
Рисунок 34. Динамика распределения запасов ОВ и азота в лесной подстилке (органогенные горизонты) и органоминеральной части почвенного профиля в сценарии культур Pinus sylvestris с регулярной схемой посадки на дерново-подбуре: средние значения показателей для соответствующих горизонтов
ЗАКЛЮЧЕНИЕ
В рамках представленной работы реализована интеграция разномасштабных имитационных моделей, учитывающих и воспроизводящих в имитационных экспериментах иерархию и пространственную неоднородность лесных экосистем со сложной структурой соподчинения и функциональными взаимосвязями между слагающими их компонентами. Система моделей параметризована для лесных экосистем Европейской части России с учётом характерного для них диапазона почвенно-климатических условий, разнообразия и сложности видового состава и пространственных структур, что формирует многообразие функциональных экологических связей. Для создания системы моделей, её параметризации и валидации использовались как ранее опубликованные литературные данные, так и результаты собственных экспериментальных исследований. Отметим, что важность пространственных измерений при изучении динамики экосистем была заявлена значительно позже (Watt, 1947), чем начались систематические попытки описать динамику популяций растений. Вплоть до недавнего времени подходы к моделированию ограничивались биометрическим количественным анализом экологических данных. Исследователи редко ставили перед собой цель всестороннего и исчерпывающего сбора данных, позволяющего строить и верифицировать модели экосистемного уровня.
В большинстве существующих к настоящему времени математических или компьютерных моделей растительных сообществ, воспроизводящих структуру крон деревьев, не учитывается возникновение асимметрии крон как результат конкуренции между деревьями за ресурсы ФАР, хотя важность решения подобной задачи очевидна (Cescatti, 1997a, 1997b). Корневая конкуренция за элементы почвенного питания в большинстве моделей также описывается в упрощённом виде, и только немногие модели в состоянии описать распределение корней древесных растений в почве в зависимости от конкуренции со стороны соседей и гетерогенности почвенных условий (Mao et al., 2015; Shanin et al., 2015a). Поэтому большинство существующих моделей, как правило, не в состоянии воспроизвести быстрые отклики корневых систем на разномасштабные изменения в окружающей среде. Недооценка пластичности крон и корневых систем в моделях может приводить к неправильной оценке интенсивности конкуренции в разных частях древостоя (как её переоценке, так и недооценке) и, как следствие, к ошибкам в расчёте продукции биомассы отдельных деревьев. Предложенная система моделей имеет адаптивный характер работы алгоритма, позволяющий воспроизвести снижение остроты конкурентного взаимодействия между отдельными деревьями в древостое за счёт пластичности их крон и корневых систем. Предлагаемый подход является компромиссным вариантом между детальными инженерными моделями, учитывающими точную структуру крон, рассеивание и повторные отражения световых лучей, но требующими большого количества входных параметров, и упрощёнными моделями, представляющими полог леса в виде нескольких слоёв, а кроны деревьев — в виде объектов с однородной внутренней структурой.
Реализация данной системы моделей позволяет воспроизводить в имитационных экспериментах пространственную структуру лесных фитоценозов (включая начальные стадии развития древостоя) и связанную с этим неоднородность почвенных условий на разных иерархических уровнях как инструмент контроля и предсказания динамики, устойчивого функционирования и биоразнообразия лесов при разных трендах их хозяйственного использования и природных изменений. Система моделей сопрягает экофизиологические процессы разного масштаба, детализация которых позволяет изучать влияние неоднородностей различного генезиса на экологические процессы и свойства растительного сообщества и почвы. Разработанная система моделей воспроизводит пространственную неоднородность, которая существенным образом влияет на динамику биогеоценоза и определяет его устойчивое функционирование в естественных условиях и при внешних воздействиях (до определённого порога интенсивности). Данная пространственно-детализированная процессная система моделей способна воспроизводить динамику лесных экосистем с учётом видовой и пространственной структуры разных ярусов растительности и её влияния через систему прямых и обратных связей на формирование мозаичности почвенных условий, что позволяет существенно улучшить понимание экосистемных процессов и их вклад в поддержание устойчивого функционирования лесов.
С помощью разработанной системы моделей в тестовых имитационных экспериментах оценена роль адаптационных механизмов в смягчении конкуренции между деревьями за свет и элементы питания. Кроме этого, показано влияние пространственной структуры древостоев на такие экосистемные услуги лесов, как сток углерода и поддержание почвенного плодородия. Также показано, что эффективность использования ресурсов в смешанных и/или разновозрастных древостоях, как правило, выше, по сравнению с одновозрастными и одновидовыми, что также подтверждается экспериментальными данными (Brassard et al., 2011). Результаты моделирования показывают, что усложнение структуры древостоев (например, усложнение их пространственной структуры, вертикальной структуры древесного яруса, увеличение его видового разнообразия) выражается в более сложном в пространственном отношении характере конкуренции за ресурсы, в том числе в более эффективном использовании имеющихся ресурсов. Так, например, имитационные эксперименты показали более высокую устойчивость смешанных древостоев к нарушениям разного рода в результате реализации этого и других механизмов, таких как эколого-ценотические стратегии видов и разделение экологических ниш, что формирует разный отклик популяций разных видов на изменение экологических условий. Как следствие, на уровне древостоя в целом это может повышать их устойчивость к воздействиям, особенно в сочетании с отмеченной выше более высокой продуктивностью смешанных древостоев.
Таким образом, разработанная система моделей за счёт реализованного в ней широкого спектра взаимосвязанных экосистемных характеристик позволяет выполнять имитационные оценки продуктивности, биогенного круговорота C и N и динамики лесных экосистем с учётом характерной для них разномасштабной пространственно-видовой структуры и детального описания процессов конкуренции в древостое. Это может быть использовано в прогнозных оценках эффективности лесопользования и других экологических задачах в наукоёмком лесоводстве и устойчивом лесном хозяйстве ближайшего будущего.
БЛАГОДАРНОСТИ
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 18-14-00362-П): сбор экспериментальных данных, параметризация и валидация системы моделей, проведение имитационных экспериментов и анализ их результатов. Разработка системы моделей выполнена в рамках темы 122040500037-6 Государственного задания ФИЦ ПНЦБИ РАН. Некоторые этапы работ по разработке отдельных блоков системы моделей выполнены ранее при финансовой поддержке Российского фонда фундаментальных исследований. В основе концепции системы моделей лежат идеи, сформулированные проф., д. б. н. А. С. Комаровым и проф., д. б. н. О. Г. Чертовым. Выражаем благодарность всем коллегам, участвовавшим в обсуждении структуры системы моделей и помогавшим в сборе данных: проф., д. б. н. М. В. Бобровскому (ИФХиБПП РАН — обособленное подразделение ФИЦ ПНЦБИ РАН); М. П. Шашкову, к. б. н. Н. В. Ивановой, к. б. н. Л. Г. Ханиной и к. б. н. В. Э. Смирнову (ИМПБ РАН — филиал ФИЦ ИПМ им. М. В. Келдыша РАН); проф., д. б. н. О. В. Смирновой, чл.‑корр. РАН Н. В. Лукиной (ЦЭПЛ РАН); проф., д. б. н. К. С. Бобковой, д. б. н. С. В. Загировой, к. б. н. А. Ф. Осипову, к. с.‑х. н. А. В. Манову (ИБ ФИЦ Коми НЦ УрО РАН); Dr. R. Mäkipää (Natural Resources Institute Finland — Luke); Л. К. Гинжул; руководству и сотрудникам Государственного природного заповедника «Калужские засеки», Приокско-Террасного государственного природного биосферного заповедника им. М. А. Заблоцкого, филиала ГКУ МО лесничества «Русский лес».
СПИСОК ЛИТЕРАТУРЫ
Абражко М. А. Реакция тонких корней ели на исключение корневой конкуренции соседних деревьев // Лесоведение. 1982. № 6. С. 41–46.
Архангельская Т. А. Температурный режим комплексного почвенного покрова. М.: ГЕОС, 2012. 282 с.
Банева Н. А. Изменение массы мелких корней ели в чистых древостоях // Лесоведение. 1980. № 1. С. 86–89.
Берлин Н. Г., Кабанов С. В., Маштаков Д. А. Вертикальная структура надземной фитомассы дубовых полезащитных лесных полос на южных чернозёмах степи правобережья Саратовской области // Вестник Алтайского государственного аграрного университета. 2015. № 5 (127). С. 87–94.
Бетехтина А. А., Большаков В. Н., Некрасова О. А., Радченко Т. А., Малыгин М. В., Дергачева М. И. Самозарастание золоотвалов: оценка микоризообразования, содержания азота и углерода в тонких корнях Betula pendula Roth. и Populus tremula L. // Экологическая и техносферная безопасность горнопромышленных регионов: Труды VII Международной научно-практической конференции 9 апреля 2019 (отв. редактор А. И. Семячков). Екатеринбург: Институт экономики УрО РАН, Уральский государственный горный университет, 2019. С. 34–39.
Бобкова К. С. Строение корневых систем древесных пород в различных типах сосновых лесов Зеленоборского стационара // Вопросы экологии сосняков Севера: Труды Коми филиала АН СССР. 1972. Т. 24. С. 52–69.
Бобкова К. С. Биологическая продуктивность хвойных лесов Европейского Северо-Востока. Л.: Наука, 1987. 156 с.
Бобкова К. С., Галенко Э. П., Загирова С. В., Патов А. И. Состав и структура древостоев коренных ельников предгорий Урала бассейна верхней Печоры // Лесоведение. 2007. № 3. С. 23–31.
Бобкова К. С., Урнышев А. П., Урнышев В. А. Вертикальное распределение фитомассы в еловых лесах европейского Северо-Востока // Лесоведение. 2000. № 3. С. 49–54.
Бобровский М. В. Лесные почвы Европейской России. М.: Тов-во научн. изд. КМК, 2010. 359 с.
Бобровский М. В., Лойко С. В. Возраст и особенности генезиса темногумусовых почв «Калужских засек» // Вестник МГУ, сер. геогр. 2019. № 5. С. 108–117.
Вакуров А. Д., Полякова А. Ф. Круговорот азота и минеральных элементов в низкопродуктивных ельниках северной тайги / Круговорот химических веществ в лесу. М.: Наука, 1982а. С. 20–43.
Вакуров Д. А., Полякова А. Ф. Круговорот азота и минеральных элементов в 35-летнем осиннике / Круговорот химических веществ в лесу. М.: Наука, 1982б. С. 44–54.
Верхоланцева Л. А., Бобкова К. С. Влияние почвенных условий на корневые системы древесных пород в еловых насаждениях подзоны северной тайги. Сыктывкар, 1972. 56 с.
Винокурова Р. И., Лобанова О. В. Специфичность распределения макроэлементов в органах древесных растений елово-пихтовых лесов Республики Марий Эл // Вестник Поволжского государственного технологического университета. Серия: Лес. Экология. Природопользование. 2011. № 2. С. 76–83.
Восточноевропейские леса: история в голоцене и современность. Кн. 1. (под ред. О. В. Смирновой). М.: Наука, 2004. 479 с.
Второва В. Н. Особенности вертикального распределения химического состава структурных компонентов ели и сосны в Подмосковье / Комплексные биогеоценотические исследования в лесах Подмосковья. М.: Наука, 1982. С. 5–20.
Герлинг Н. В., Тарасов С. И. Закономерности ассимиляции диоксида углерода хвоей пихты сибирской в области высоких интенсивностей фотосинтетически активной радиации // Биодиагностика состояния природных и природно-техногенных систем: Материалы ХVIII Всероссийской научно-практической конференции c международным участием. Киров: Вятский государственный университет, 2020. С. 111.
Гиниятуллин Р. Х., Кулагин А. Ю. Состояние корневой системы берёзы повислой (Betula pendula Roth.) в условиях Стерлитамакского промышленного центра // Вестник Удмуртского университета. Серия «Биология. Науки о Земле». 2012. № 4. С. 21–28.
Грабарник П. Я., Чертов О. Г., Чумаченко С. И., Шанин В. Н., Ханина Л. Г., Бобровский М. В., Быховец С. С., Фролов П. В. Интеграция имитационных моделей для комплексной оценки экосистемных услуг лесов: методические подходы // Математическая биология и биоинформатика. 2019а. Т. 14. № 2. С. 488–499. DOI: 10.17537/2019.14.488.
Грабарник П. Я., Шанин В. Н., Чертов О. Г., Припутина И. В., Быховец С. С., Петропавловский Б. С., Фролов П. В., Зубкова Е. В., Шашков М. П., Фролова Г. Г. Моделирование динамики лесных экосистем как инструмент прогнозирования и управления лесами // Лесоведение. 2019б. № 6. С. 488–500. DOI: 10.1134/S0024114819030033.
Гульбе Я. И., Ермолова Л. С., Рождественский С. Г., Уткин А. И., Цельникер Ю. Л. Вертикальное распределение поверхности листьев и световой режим в лиственных молодняках южной тайги // Лесоведение. 1983. № 2. С. 21–29.
Дейнеко И. П., Фаустова Н. М. Элементный и групповой химический состав коры и древесины осины // Химия растительного сырья. 2015. № 1. С. 51–62. DOI: 10.14258/jcprm.201501461.
Диагнозы и ключи возрастных состояний лесных растений. Деревья и кустарники: методические разработки для студентов биологических специальностей. Ч. 1 (под ред. О. В. Смирновой). М.: Изд-во «Прометей» МГПИ им. В. И. Ленина, 1989. 102 с.
Дымов А. А., Бобкова К. С., Тужилкина В. В., Ракина Д. А. Растительный опад в коренном ельнике и лиственно-хвойных насаждениях // Известия высших учебных заведений. Лесной журнал. 2012. № 3. С. 7–18.
Евневич Т. В., Савиковский И. А. Расчёт прямой солнечной радиации и коэффициента прозрачности атмосферы // Метеорология и гидрология. 1989. № 5. С. 106–109.
Желдак В. И., Атрохин В. Г. Лесоводство, ч. I. М.: ВНИИЛМ, 2002. 336 с.
Жукова Л. А. Концепция фитогенных полей и современные аспекты их изучения // Известия Самарского научного центра Российской академии наук. 2012. Т. 14. № 1–6. С. 1462–1465.
Исаев А. С., Овчинникова Т. М., Суховольский В. Г. Распределение фитомассы деревьев и насаждений по фракциям: модель конкуренции // Проблемы экологического мониторинга и моделирования экосистем. 2007. Т. 21. С. 232–250.
Казимиров Н. И., Морозова Р. М. Биологический круговорот веществ в ельниках Карелии. Л.: Наука, 1973. 175 с.
Каплина Н. Ф., Кулакова Н. Ю. Фитомасса и запасы углерода и азота в контрастных по продуктивности нагорных дубравах южной лесостепи // Аридные экосистемы. 2021. Т. 27. № 1 (86). С. 35–42. DOI: 10.24411/1993-3916-2021-10135.
Карманова И. В., Судницина Т. Н., Ильина Н. А. Пространственная структура сложных сосняков. М.: Наука, 1987. 100 с.
Карпачевский Л. О. Лес и лесные почвы. М.: Лесн. пром-сть, 1981. 264 с.
Карпечко Ю. В. Оценка пространственной и временной неоднородности задержания жидких осадков пологом леса // Лесоведение. 1997. № 4. С. 64–70.
Классификация и диагностика почв России (отв. ред. Г. В. Добровольский). Смоленск: Ойкумена, 2004. 341 с.
Колобов А. Н. Моделирование пространственно-временной динамики древесных сообществ: Дисс. … канд. физ.‑мат. наук (спец. 03.01.02). Биробиджан: Институт комплексного анализа региональных проблем ДВО РАН, 2013. 133 с.
Колобов А. Н., Лонкина Е. С., Фрисман Е. Я. Моделирование и анализ горизонтальной структуры смешанных древостоев (на примере пробных площадей заповедника «Бастак» в Среднем Приамурье) // Сибирский лесной журнал. 2015. № 3. С. 45–56. DOI: 10.15372/SJFS20150305.
Комаров А. С. Простые структуры растительного покрова, устойчивые к внешним нарушениям / Взаимодействующие Марковские процессы и их применение к математическому моделированию биологических систем. Пущино: ОНТИ НЦБИ АН СССР, 1982. С. 136–143.
Комаров А. С. Пространственные индивидуально-ориентированные модели лесных экосистем // Лесоведение. 2010. № 2. С. 60–68.
Коренные еловые леса Севера: биоразнообразие, структура, функции (отв. ред. К. С. Бобкова, Э. П. Галенко). СПб.: Наука, 2006. 337 с.
Корзухин М. Д., Выгодская Н. Н., Милюкова И. М., Татаринов Ф. А., Цельникер Ю. Л. Применение объединенной модели фотосинтеза и устьичной проводимости к анализу ассимиляции углерода елью и лиственницей в лесах России // Физиология растений. 2004. Т. 51. № 3. С. 341–354.
Корзухин М. Д., Цельникер Ю. Л. Анализ распространения и чистой первичной продукции четырёх лесных пород деревьев в России с помощью экофизиологической модели // Проблемы экологического мониторинга и моделирования экосистем. 2009. Т. 22. С. 92–123.
Корзухин М. Д., Цельникер Ю. Л. Модельный анализ современных ареалов лесных древесных пород на территории России и их вариаций при возможных изменениях климата // Проблемы экологического мониторинга и моделирования экосистем. 2010. Т. 23. С. 249–268.
Корзухин М. Д., Цельникер Ю. Л., Семенов С. М. Экофизиологическая модель первичной продуктивности древесных растений и оценки климатических пределов их произрастания // Метеорология и гидрология. 2008. № 12. С. 56–69.
Коротков В. Н. Новая парадигма в лесной экологии // Биологические науки. 1991. № 8. С. 7–19.
Лащинский Н. Н. Структура и динамика сосновых лесов Нижнего Приангарья. М.: Наука, 1981. 272 с.
Лебедев Е. В. Продуктивность берёзы белой на уровне организма в онтогенезе в европейской части России // Известия Оренбургского государственного аграрного университета. 2012а. № 4 (36). С. 18–22.
Лебедев Е. В. Продуктивность фотосинтеза и минеральное питание липы мелколистной на уровне организма в онтогенезе в среднем Поволжье // Вестник РУДН, серия Экология и безопасность жизнедеятельности. 2012б. № 4. С. 5–10.
Лебедев Е. В. Биологическая продуктивность дуба черешчатого на уровне организма в онтогенезе в Европейской части России // Лесной вестник. 2013. № 3. С. 28–33.
Лебедев В. М., Лебедев Е. В. Морфологические, функциональные и физиологические особенности активной части корневой системы лесообразующих пород Волго-Вятского региона // Агрохимия. 2011. № 4. С. 38–44.
Лебедев В. М., Лебедев Е. В. Взаимосвязь биологической продуктивности и поглотительной деятельности корней хвойных пород в онтогенезе в зоне южной тайги России // Агрохимия. 2012. № 8. С. 9–17.
Лебедев С. В., Чумаченко С. И. Подеревная модель динамики многовидового разновозрастного насаждения (PIXTA) // Вестник Московского государственного университета леса. Лесной вестник. 2011. № 7 (83). С. 71–78.
Лозинов Г. Л. Особенности пространственного распределения подземных частей растений в лесных биогеоценозах Подмосковья // Лесоведение. 1980. № 1. С. 58–63.
Лукина Н. В. Запас фитомассы древостоев сосняков лишайниковых на северном пределе их распространения // Лесоведение. 1996. № 3. С. 28–37.
Лукина Н. В., Никонов В. В., Райтио Х. Химический состав хвои сосны на Кольском полуострове // Лесоведение. 1994. № 6. С. 10–21.
Лукьянец В. Б. Содержание азота и зольных элементов в листьях дуба различного географического происхождения // Лесоведение. 1980. № 1. С. 52–57.
Лукьященко К. И., Архангельская Т. А. Моделирование температуропроводности почв различного гранулометрического состава // Почвоведение. 2018. № 2. С. 179–186. DOI: 10.7868/S0032180X18020053.
Матвиенко А. И. Влияние азота на минерализацию углерода в почвах под лиственницей сибирской и сосной обыкновенной: Дисс. … канд. биол. наук (спец. 03.02.08). Красноярск: Институт леса им. В. Н. Сукачева СО РАН, ФИЦ «Красноярский научный центр СО РАН», 2017. 147 с.
Медведев И. Ф., Деревягин С. С., Козаченко М. А., Гусакова Н. Н. Оценка содержания химических элементов в древесине различных пород деревьев // Аграрный научный журнал. 2015. № 11. С. 12–14.
Мигунова Е. С. Леса и лесные земли (количественная оценка взаимосвязей). М.: Экология, 1993. 364 с.
Моделирование динамики органического вещества в лесных экосистемах (под ред. В. Н. Кудеярова). М.: Наука, 2007. 380 с.
Молчанов А. А., Полякова А. Ф. Продуктивность органической массы в сосняках сфагновых / Продуктивность органической и биологической массы леса. М.: Наука, 1974. С. 43–77.
Молчанов А. А., Полякова А. Ф. Характеристика основных типов леса / Основные типы биогеоценозов северной тайги. М.: Наука, 1977. С. 44–203.
Морозова Р. М. Химический состав растений еловых и берёзовых лесов Карелии / Лесные растительные ресурсы Южной Карелии. Петрозаводск: Карелия, 1971. С. 57–66.
Морозова Р. М. Минеральный состав растений лесов Карелии. Петрозаводск: Госкомиздат, 1991. 100 с.
Никонов В. В., Лукина Н. В., Смирнова Е. В., Исаева Л. Г. Влияние ели и сосны на формирование первичной продуктивности нижними ярусами хвойных лесов Кольского полуострова // Ботанический журнал. 2002. Т. 87. № 8. С. 112–124.
Новицкая Ю. Е. Особенности физиолого-биохимических процессов в хвое и побегах ели в условиях Севера. Л.: Наука, 1971. 117 с.
Носова Л. М. Особенности вертикального распределения фитомассы липы разного возраста в лесных биогеоценозах // Бюллетень Московского общества испытателей природы. Отдел биологический. 1970. Т. LXXV(3). С. 96–107.
Носова Л. М., Холопова Л. Б. Особенности обмена веществ между растительностью и почвой в искусственных насаждениях сосны на дерново-подзолистых почвах / Общие проблемы биогеоценологии. М.: Наука, 1990. С. 252–266.
Орлова М. А., Лукина Н. В., Камаев И. О., Смирнов В. Э., Кравченко Т. В. Мозаичность лесных биогеоценозов и плодородие почв // Лесоведение. 2011. № 6. С. 39–48.
Оськина Н. В. Содержание азота и зольных элементов в надземной фитомассе культур сосны обыкновенной Владимирской, Ульяновской и Куйбышевской областей / Биологическая продуктивность лесов Поволжья. М.: Наука, 1982. С. 7–11.
Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. М.: Энергоатомиздат, 1984. 152 c.
Портнов А. М., Быховец С. С., Дин Е. С., Иванова Н. В., Фролов П. В., Шанин В. Н., Шашков М. П. Количественная оценка размеров окон в пологе старовозрастного широколиственного леса наземными и дистанционными методами // Математическое моделирование в экологии. Материалы Седьмой Национальной научной конференции с международным участием, 9–12 ноября 2021 г. Пущино: ФИЦ ПНЦБИ РАН, 2021. С. 99–102.
Припутина И. В., Фролова Г. Г., Быховец С. С., Шанин В. Н., Лебедев В. Г., Шестибратов К. А. Моделирование продуктивности лесных плантаций при разных схемах пространственного размещения деревьев // Математическая биология и биоинформатика. 2016. Т. 11. № 2. С. 245–262. DOI: 10.17537/2016.11.245.
Припутина И. В., Чертов О. Г., Фролов П. В., Шанин В. Н., Грабарник П. Я. Включение ризосферного прайминг-эффекта в модель динамики органического вещества почв Romul_Hum: подходы и результаты предварительного тестирования // Математическое моделирование в экологии. Материалы Седьмой Национальной научной конференции с международным участием, 9–12 ноября 2021 г. Пущино: ФИЦ ПНЦБИ РАН, 2021. С. 106–108.
Пугачевский A. B. Ценопопуляции ели. Структура, динамика, факторы регуляции. Минск: Наука и техника, 1992. 206 с.
Работнов Т. А. Азот в наземных биогеоценозах / Структурно-функциональная организация биогеоценозов. М.: Наука, 1980. С. 69–90.
Ремезов Н. П., Быкова Л. Н., Смирнова К. М. Потребление и круговорот азота и зольных элементов в лесах Европейской части СССР. М.: Издательство Московского университета, 1959. 284 с.
Ремезов Н. П., Погребняк П. С. Лесное почвоведение. М.: Лесная промышленность, 1965. 324 с.
Решетникова Т. В. Лесные подстилки как депо биогенных элементов // Вестник Красноярского государственного аграрного университета. 2011. № 12. С. 74–81.
Росс Ю. К. Радиационный режим и архитектоника растительного покрова. Л.: Гидрометеоиздат, 1975. 342 с.
Русанова Г. В. Биологическая продуктивность и содержание химических элементов в фитомассе ельника-зеленомошника / Продуктивность и круговорот элементов в фитоценозах севера. Л.: Наука, 1975. С. 30–51.
Санников С. Н., Санникова Н. С. Лес как подземно-сомкнутая дендроценоэкосистема // Сибирский лесной журнал. 2014. № 1. С. 25–34.
Секретенко О. П. Анализ пространственной структуры и эффектов взаимодействия в биологических сообществах. Автореф. дис. … к.ф.‑м.н. Красноярск, 2001. 22 с.
Смеян Н. И., Романова Т. А., Туренков Н. И., Тихонов С. А., Балханова К. В. Подзолистые почвы Белорусской ССР / Подзолистые почвы запада Европейской части СССР. М.: Колос, 1977. С. 31–109.
Справочник по древесине (под ред. Б. Н. Уголева). М.: Лесная промышленность, 1989. 296 с.
Стаканов В. Д. Распределение органического вещества в различных частях деревьев сосны обыкновенной // Лесоведение. 1990. № 4. С. 25–33.
Столяров Д. П., Полубояринов В. Н., Минаев В. Н., Декатов Н. Н., Некрасова Г. Н. Рекомендации по оценке строения, товарной структуры и качества древесины разновозрастных ельников с целью организации выборочного хозяйства. Л.: НИИ лесного хозяйства, 1989. 56 с.
Судачкова Н. Е., Милютина И. Л., Семенова Г. П. Специфика метаболизма лиственницы сибирской и лиственницы Гмелина в различных экологических условиях // Хвойные бореальной зоны. 2003. Т. 21. № 1. С. 54–60.
Сукцессионные процессы в заповедниках России и проблемы сохранения биологического разнообразия (под ред. О. В. Смирновой, Е. С. Шапошникова). СПб: РБО, 1999. 549 с.
Терехов Г. Г., Усольцев В. А. Морфоструктура насаждений и корненасыщенность ризосферы культур ели сибирской и вторичного лиственного древостоя на Среднем Урале как характеристика их конкурентных отношений // Хвойные бореальной зоны. 2010. Т. XXVII. № 3–4. С. 330–335.
Тихонова Е. В., Тихонов Г. Н. Мозаичность хвойно-широколиственных лесов Валуевского лесопарка // Вопросы лесной науки. 2021. Т. 4. № 3. Статья № 88. DOI: 10.31509/2658-607x- 202143-88.
Туменбаева А. Р., Сарсекова Д. Н., Боранбай Ж. Содержание углерода в различных элементах фитомассы берёзы повислой (Betula pendula Roth.) в зелёном поясе города Астаны // Международный научно-исследовательский журнал. 2018. № 7 (73). С. 80–84. DOI: 10.23670/IRJ.2018.73.7.016.
Усольцев В. А. Фитомасса лесов Северной Евразии: нормативы и элементы географии. Екатеринбург: УрО РАН, 2002. 762 с.
Усольцев В. А. Вертикально-фракционная структура фитомассы деревьев. Исследование закономерностей. Екатеринбург: УГЛТУ, 2013а. 603 с.
Усольцев В. А. Продукционные показатели и конкурентные отношения деревьев. Исследование зависимостей. Екатеринбург: УГЛТУ, 2013б. 553 с.
Усольцев В. А. Фитомасса модельных деревьев лесообразующих пород Евразии: база данных, климатически обусловленная география, таксационные нормативы. Екатеринбург: Уральский государственный лесотехнический университет, 2016. 336 с.
Уткин А. И., Ермолова Л. С., Уткина И. А. Площадь поверхности лесных растений: сущность, параметры, использование. М.: Наука, 2008. 292 с.
Фёдоров С. Ф. Исследование элементов водного баланса в лесной зоне Европейской территории СССР. Л.: Гидрометеоиздат, 1977. 264 с.
Хавроньин А. В., Кретинин В. М., Дубовская Л. В. Биологическая аккумуляция питательных элементов в полезащитных лесных полосах на обыкновенном черноземе / Вопросы лесной биогеоценологии, экологии и охраны природы в степной зоне. Межвузовский сборник. Выпуск 2. Куйбышев: Куйбышевский государственный университет, 1977. С. 42–49.
Хораськина Ю. С., Комаров А. С., Безрукова М. Г., Жиянски М. К. Моделирование динамики кальция в органических горизонтах почвы // Компьютерные исследования и моделирование. 2010. Т. 2. № 1. С. 103–110. DOI: 10.20537/2076-7633-2010-2-1-103-110.
Цельникер Ю. Л., Малкина И. С., Гурцев А. И., Николаев Д. К. Количественная оценка светового режима по морфоструктурным показателям крон подроста ели // Лесоведение. 1999. № 4. С. 64–69.
Цельникер Ю. Л., Корзухин М. Д., Семенов С. М. Модельный анализ широтного распределения продуктивности лесных пород России // Лесоведение. 2010. № 2. С. 36–45.
Цельникер Ю. Л., Корзухин М. Д., Суворова Г. Г., Янькова Л. С., Копытова Л. Д., Филиппова А. К. Анализ влияния факторов среды на фотосинтез хвойных Предбайкалья // Проблемы экологического мониторинга и моделирования экосистем. 2007. Т. 21. С. 265–292.
Чертов О. Г. Экология лесных земель. Почвенно-экологическое исследование лесных местообитаний. М.: Наука, 1981. 192 с.
Чертов О. Г., Комаров А. С., Быховец С. С., Бхатти Д. С. Различие экологических стратегий хвойных пород в европейских и канадских бореальных лесах // Биосфера. 2015. Т. 7. № 3. С. 328–337.
Чертов О. Г., Грабарник П. Я., Шанин В. Н., Быховец С. С., Петропавловский Б. С., Припутина И. В., Фролов П. В., Зубкова Е. В. Динамические модели наземных экосистем для количественной оценки продуктивности растительности // Растительные ресурсы. 2019. № 2. С. 151–169. DOI: 10.1134/S0033994619020031.
Шанин В. Н., Грабарник П. Я., Быховец С. С., Чертов О. Г., Припутина И. В., Шашков М. П., Иванова Н. В., Стаменов М. Н., Фролов П. В., Зубкова Е. В., Ручинская Е. В. Параметризация модели продукционного процесса для доминирующих видов деревьев Европейской части РФ в задачах моделирования динамики лесных экосистем // Математическая биология и биоинформатика. 2019. Т. 14. № 1. С. 54–76. DOI: 10.17537/2019.14.54.
Шанин В. Н., Шашков М. П., Иванова Н. В., Быховец С. С., Грабарник П. Я. Исследование структуры древостоев и микроклиматических условий под пологом леса на постоянной пробной площади в Приокско-террасном заповеднике / Труды Приокско-террасного заповедника. Вып. 7. М.: Товарищество научных изданий КМК, 2018. С. 68–80.
Шанин В. Н., Шашков М. П., Иванова Н. В., Грабарник П. Я. Влияние конкуренции в пологе леса на пространственную структуру древостоев и форму крон доминантов древесного яруса на примере лесов европейской части России // Russian Journal of Ecosystem Ecology. 2016. Т. 1. № 4. DOI: 10.21685/2500-0578-2016-4-5.
Швиденко А. З., Щепащенко Д. Г., Нильссон С., Булуй Ю. И. Таблицы и модели роста и продуктивности основных лесообразующих пород Северной Евразии (нормативно-справочные материалы). М.: Федеральное агентство лесного хозяйства. Международный институт прикладного системного анализа, 2008. 886 с.
Шеин Е. В. Курс физики почв. М.: Издательство МГУ, 2005. 432 с.
Ярмишко В. Т. Вертикально-фракционная структура надземной фитомассы Pinus sylvestris L. на северном пределе распространения в условиях атмосферного загрязнения // Растительные ресурсы. 1999. Т. 35. № 1. С. 3–12.
Alberti G., Candido P., Peressotti A., Turco S., Piussi P., Zerbi G. Aboveground biomass relationships for mixed ash (Fraxinus excelsior L. and Ulmus glabra Hudson) stands in Eastern Prealps of Friuli Venezia Giulia (Italy) // Annals of Forest Science. 2005. Vol. 62. No. 8. P. 831–836. DOI: 10.1051/forest:2005089.
Aldea J., Ruiz‑Peinado R., del Río M., Pretzsch H., Heym M., Brazaitis G., Jansons A., Metslaid M., Barbeito I., Bielak K., Granhus A., Holm S.‑O., Nothdurft A., Sitko R., Löf M. Species stratification and weather conditions drive tree growth in Scots pine and Norway spruce mixed stands along Europe // Forest Ecology and Management. 2021. Vol. 481. ID 118697. DOI: 10.1016/j.foreco.2020.118697.
Amichev B. Y., Johnston M., van Rees K. C. J. Hybrid poplar growth in bioenergy production systems: Biomass prediction with a simple process-based model (3PG) // Biomass and Bioenergy. 2010. Vol. 34. No. 5. P. 687–702. DOI: 10.1016/j.biombioe.2010.01.012.
Appleby R. F., Davies W. J. A possible evaporation site in the guard cell wall and the influence of leaf structure on the humidity response by stomata of woody plants // Oecologia. 1983. Vol. 56. No. 1. P. 30–40. DOI: 10.1007/BF00378214.
Arii K., Parrott L. Examining the colonization process of exotic species varying in competitive abilities using a cellular automaton model // Ecological Modelling. 2006. Vol. 199. No. 3. P. 219–228. DOI: 10.1016/j.ecolmodel.2006.05.032.
Arkhangelskaya T. A., Gvozdkova A. A. Thermal diffusivity of peat-sand mixtures // IOP Conference Series: Earth and Environmental Science. 2019. Vol. 368. ID 012005. DOI: 10.1088/1755-1315/368/1/012005.
Aschan G., Wittmann C., Pfanz H. Age-dependent bark photosynthesis of aspen twigs // Trees. 2001. Vol. 15. P. 431–437. DOI: 10.1007/s004680100120.
Badache M., Eslami‑Nejad P., Ouzzane M., Aidoun Z., Lamarche L. A new modeling approach for improved ground temperature profile determination // Renewable Energy. 2016. Vol. 85. P. 436–444. DOI: 10.1016/j.renene.2015.06.020.
Badía D., López‑García S., Martí C., Ortíz‑Perpiñá O., Girona‑García A., Casanova‑Gascón J. Burn effects on soil properties associated to heat transfer under contrasting moisture content // Science of the Total Environment. 2017. Vol. 601–602. P. 1119–1128. DOI: 10.1016/j.scitotenv.2017.05.254.
Balboa‑Murias M. A., Rojo A., Álvarez J. G., Merino A. Carbon and nutrient stocks in mature Quercus robur L. stands in NW Spain // Annals of Forest Science. 2006. Vol. 63. No. 5. P. 557–565. DOI: 10.1051/forest:2006038.
Baldocchi D. D., Law B. E., Anthoni P. M. On measuring and modeling energy fluxes above the floor of a homogeneous and heterogeneous conifer forest // Agricultural and Forest Meteorology. 2000. Vol. 102. No. 2–3. P. 187–206. DOI: 10.1016/S0168-1923(00)00098-8.
Balland V., Pollacco J. A. P., Arp P. A. Modeling soil hydraulic properties for a wide range of soil conditions // Ecological Modelling. 2008. Vol. 219. No. 3–4. P. 300–316. DOI: 10.1016/j.ecolmodel.2008.07.009.
Barbeito I., Dassot M., Bayer D., Collet C., Drössler L., Löf M., del Rio M., Ruiz‑Peinado R., Forrester D. I., Bravo‑Oviedo A., Pretzsch H. Terrestrial laser scanning reveals differences in crown structure of Fagus sylvatica in mixed vs. pure European forests // Forest Ecology and Management. 2017. Vol. 405. P. 381–390. DOI: 10.1016/j.foreco.2017.09.043.
Bauer G., Schulze E.‑D., Mund M. Nutrient contents and concentrations in relation to growth of Picea abies and Fagus sylvatica along a European transect // Tree Physiology. 1997. Vol. 17. No. 12. P. 777–786. DOI: 10.1093/treephys/17.12.777.
Bayer D., Reischl A., Rötzer T., Pretzsch H. Structural response of black locust (Robinia pseudoacacia L.) and small-leaved lime (Tilia cordata Mill.) to varying urban environments analyzed by terrestrial laser scanning: Implications for ecological functions and services // Urban Forestry & Urban Greening. 2018. Vol. 35. P. 129–138. DOI: 10.1016/j.ufug.2018.08.011.
Belyazid S., Sverdrup H., Kurz D., Braun S. Exploring ground vegetation change for different deposition scenario and methods of estimating critical loads or biodiversity using ForSAFE‑VEG model in Switzerland and Sweden // Water, Air and Soil Pollution. 2011. Vol. 216. P. 289–317. DOI: 10.1007/s11270-010-0534-6.
Berger U., Piou C., Schiffers K., Grimm V. Competition among plants: Concepts, individual-based modeling approaches, and a proposal for a future research strategy // Perspectives in Plant Ecology, Evolution and Systematics. 2008. Vol. 9. No. 3–4. P. 121–135. DOI: 10.1016/j.ppees.2007.11.002.
Bielak K., Dudzińska M., Pretzsch H. Mixed stands of Scots pine (Pinus sylvestris L.) and Norway spruce [Picea abies (L.) Karst] can be more productive than monocultures. Evidence from over 100 years of observation of long-term experiments // Forest Systems. 2014. Vol. 23. No. 3. P. 573–789. DOI: 10.5424/fs/2014233-06195.
Bocock K. L. Changes in the amounts of dry matter, nitrogen, carbon and energy in decomposing woodland leaf litter in relation to the activities of the soil fauna. Journal of Ecology. 1964. Vol. 52. No. 2. P. 273–284. DOI: 10.2307/2257595.
Bolte A., Villanueva I. Interspecific competition impacts on the morphology and distribution of fine roots in European beech (Fagus sylvatica L.) and Norway spruce (Picea abies (L.) Karst.) // European Journal of Forest Research. 2006. Vol. 125. P. 15–26. DOI: 10.1007/s10342-005-0075-5.
Bonten L. T. C., Groeneberg J. E., Meesenburg H., De Vries W. Using advanced surface complexation models for modelling soil chemistry under forests: Solling forest, Germany // Environmental Pollution. 2011. Vol. 159. No. 10. P. 2831–2839. DOI: 10.1016/j.envpol.2011.05.002.
Brandtberg P. ‑O., Bengtsson J., Lundkvist H. Distributions of the capacity to take up nutrients by Betula spp. and Picea abies in mixed stands // Forest Ecology and Management. 2004. Vol. 198. No. 1–3. P. 193–208. DOI: 10.1016/j.foreco.2004.04.012.
Brassard B. W., Chen H. Y. H., Bergeron Y., Paré D. Differences in fine root productivity between mixed- and single-species stands // Functional Ecology. 2011. Vol. 25. No. 1. P. 238–246. DOI: 10.1111/j.1365-2435.2010.01769.x.
Braun S., Flückiger W. Soil amendments for plantings of urban trees // Soil and Tillage Research. 1998. Vol. 49. No. 3. P. 201–209. DOI: 10.1016/S0167-1987(98)00172-X.
Bréda N., Granier A., Barataud F., Moyne C. Soil water dynamics in an oak stand. I. Soil moisture, water potentials and water uptake by roots // Plant and Soil. 1995. Vol. 172. No. 1. P. 17–27. DOI: 10.1007/BF00020856.
Bristow K. L., Campbell G. S. On the relationship between incoming solar radiation and daily maximum and minimum temperature // Agricultural and Forest Meteorology. 1984. Vol. 31. No. 2. P. 159–166. DOI: 10.1016/0168-1923(84)90017-0.
Brunner A. A light model for spatially explicit forest stand models // Forest Ecology and Management. 1998. Vol. 107. No. 1–3. P. 19–46. DOI: 10.1016/S0378-1127(97)00325-3.
Brunner I., Bakker M. R., Björk R. G., Hirano Y., Lukac M., Aranda X., Børja I., Eldhuset T. D., Helmisaari H.‑S., Jourdan C., Konôpka B., López B. C., Pérez C. M., Persson H., Ostonen I. Fine-root turnover rates of European forests revisited: an analysis of data from sequential coring and ingrowth cores // Plant and Soil. 2013. Vol. 362. P. 357–372. DOI: 10.1007/s11104-012-1313-5.
Büttner V., Leuschner C. Spatial and temporal patterns of fine root abundance in a mixed oak-beech forest // Forest Ecology and Management. 1994. Vol. 70. No. 1–3. P. 11–21. DOI: 10.1016/0378-1127(94)90071-X.
Campbell G. S. A simple method for determining unsaturated conductivity from moisture retention data // Soil Science. 1974. Vol. 117. No. 6. P. 311–314. DOI: 10.1097/00010694-197406000-00001.
Campbell G. S. Soil physics with BASIC: transport models for soil-plant systems. Elsevier Science, 1985. 150 p.
Campbell G. S. Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination angle distribution // Agricultural and Forest Meteorology. 1986. Vol. 36. No. 4. P. 317–321. DOI: 10.1016/0168-1923(86)90010-9.
Casper B. B., Schenk H. J., Jackson R. B. Defining a plant’s belowground zone of influence // Ecology. 2003. Vol. 84. No. 9. P. 2313–2321. DOI: 10.1890/02-0287.
Cavard X., Bergeron Y., Chen H. Y. H., Paré D., Laganière J., Brassard B. Competition and facilitation between tree species change with stand development // Oikos. 2011. Vol. 120. No. 11. P. 1683–1695. DOI: 10.1111/j.1600-0706.2011.19294.x.
Cescatti A. Modelling the radiative transfer in discontinuous canopies of asymmetric crowns. I. Model structure and algorithms // Ecological Modelling. 1997a. Vol. 101. No. 2–3. P. 263–274. DOI: 10.1016/S0304-3800(97)00050-1.
Cescatti A. Modelling the radiative transfer in discontinuous canopies of asymmetric crowns. II. Model testing and application in a Norway spruce stand // Ecological Modelling. 1997b. Vol. 101. No. 2–3. P. 275–284. DOI: 10.1016/S0304-3800(97)00055-0.
Chalhoub M., Bernier M., Coquet Y., Philippe M. A simple heat and moisture transfer model to predict ground temperature for shallow ground heat exchangers // Renewable energy. 2017. Vol. 103. P. 295–307. DOI: 10.1016/j.renene.2016.11.027.
Chenlemuge T., Hertel D., Dulamsuren C., Khishigjargal M., Leuschner C., Hauck M. Extremely low fine root biomass in Larix sibirica forests at the southern drought limit of the boreal forest // Flora. 2013. Vol. 208. No. 8–9. P. 488–496. DOI: 10.1016/j.flora.2013.08.002.
Chertov O. G., Komarov A. S., Nadporozhskaya M. A., Bykhovets S. S., Zudin S. L. ROMUL — a model of forest soil organic matter dynamics as a substantial tool for forest ecosystem modelling // Ecological Modelling. 2001. Vol. 138. No. 1–3. P. 289–308. DOI: 10.1016/S0304-3800(00)00409-9.
Chertov O., Komarov A., Shaw C., Bykhovets S., Frolov P., Shanin V., Grabarnik P., Priputina I., Zubkova E., Shashkov M. Romul_Hum — A model of soil organic matter formation coupling with soil biota activity. II. Parameterisation of the soil food web biota activity // Ecological Modelling. 2017a. Vol. 345. P. 125–139. DOI: 10.1016/j.ecolmodel.2016.10.024.
Chertov O., Shaw C., Shashkov M., Komarov A., Bykhovets S., Shanin V., Grabarnik P., Frolov P., Kalinina O., Priputina I., Zubkova E. Romul_Hum model of soil organic matter formation coupled with soil biota activity. III. Parameterisation of earthworm activity // Ecological Modelling. 2017b. Vol. 345. P. 140–149. DOI: 10.1016/j.ecolmodel.2016.06.013.
Chertov O. G., Komarov A. S., Tsiplianovsky A. V. A combined simulation model of Scots pine, Norway spruce and Silver birch ecosystems in European boreal zone // Forest Ecology and Management. 1999. Vol. 116. No. 1–3. P. 189–206. DOI: 10.1016/S0378-1127(98)00456-3.
Chertov O., Kuzyakov Y., Priputina I., Frolov P., Shanin V., Grabarnik P. Modelling the rhizosphere priming effect in combination with soil food webs to quantify interaction between living plant, soil biota and soil organic matter // Plants. 2022. Vol. 11. No. 19. ID 2605. DOI: 10.3390/plants11192605.
Chumachenko S. I., Korotkov V. N., Palenova M. M., Politov D. V. Simulation modeling of long-term stand dynamics at different scenarios of forest management for coniferous-broad-leaved forests // Ecological Modelling. 2003. Vol. 170. No. 2–3. P. 345–362. DOI: 10.1016/S0304-3800(03)00238-2.
Collalti A., Perugini L., Santini M., Chiti T., Nolè A., Matteucci G., Valentini R. A process-based model to simulate growth in forests with complex structure: Evaluation and use of 3D‑CMCC forest ecosystem model in a deciduous forest in Central Italy // Ecological Modelling. 2014. Vol. 272. P. 362–378. DOI: 10.1016/j.ecolmodel.2013.09.016.
Coops N. C., Waring R. H., Law B. E. Assessing the past and future distribution and productivity of ponderosa pine in the Pacific Northwest using a process model, 3-PG // Ecological Modelling. 2005. Vol. 183. No. 1. P. 107–124. DOI: 10.1016/j.ecolmodel.2004.08.002.
Cosby B. J., Ferrier R. C., Jenkins A., Wright R. F. Modelling the effects of acid deposition: refinements, adjustments and inclusion of nitrogen dynamics in the MAGIC model // Hydrology and Earth System Sciences. 2001. Vol. 5. No. 3. P. 499–517. DOI: 10.5194/hess-5-499-2001.
Cosby B. J., Hornberger G. M., Clapp R. B., Ginn T. A statistical exploration of the relationships of soil moisture characteristics to the physical properties of soils // Water Resources Research. 1984. Vol. 20. No. 6. P. 682–690. DOI: 10.1029/WR020i006p00682.
Dahlhausen J., Biber P., Rötzer T., Uhl E., Pretzsch H. Tree species and their space requirements in six urban environments worldwide // Forests. 2016. Vol. 7. No. 6. ID 111. DOI: 10.3390/f7060111.
Daikoku K., Hattori S., Deguchi A., Aoki Y., Miyashita M., Matsumoto K., Akiyama J., Iida S., Toba T., Fujita Y., Ohta T. Influence of evaporation from the forest floor on evapotranspiration from the dry canopy // Hydrological Processes. 2008. Vol. 22. No. 20. P. 4083–4096. DOI: 10.1002/hyp.7010.
Daniels R. F., Burkhart H. E., Clason T. R. A comparison of competition measures for predicting growth of loblolly pine trees // Canadian Journal of Forest Research. 1986. Vol. 16. No. 6. P. 1230–1237. DOI: 10.1139/x86-218.
Danilin I. M., Tselitan I. A. Dynamics of forest ecosystems regenerated on burned and harvested areas in mountain regions of Siberia: Characteristics of biological diversity, structure and productivity // Siberian Journal of Forest Science. 2016. No. 6. P. 60–72. DOI: 10.15372/SJFS20160606.
Dannenmann M., Simon J., Gasche R., Holst J., Naumann P. S., Kögel‑Knabner I., Knicker H., Mayer H., Schloter M., Pena R., Polle A., Rennenberg H., Papen H. Tree girdling provides insight on the role of labile carbon in nitrogen partitioning between soil microorganisms and adult European beech // Soil Biology and Biochemistry. 2009. Vol. 41. No. 8. P. 1622–1631. DOI: 10.1016/j.soilbio.2009.04.024.
Dauer J., Withington J., Oleksyn J., Chorover J., Chadwick O., Reich P., Eissenstat D. A scanner-based approach to soil profile-wall mapping of root distribution // Dendrobiology. 2009. Vol. 62. P. 35–40.
De Jaegere T., Hein S., Claessens H. A. A review of the characteristics of small-leaved lime (Tilia cordata Mill.) and their implications for silviculture in a changing climate // Forests. 2016. Vol. 7. No. 3. ID 56. DOI: 10.3390/f7030056.
Dhiedt E., Baeten L., De Smedt P., Jaroszewicz B., Verheyen K. Tree neighbourhood-scale variation in topsoil chemistry depends on species identity effects related to litter quality // European Journal of Forest Research. 2022. Vol. 141. P. 1163–1176. DOI: 10.1007/s10342-022-01499-9.
Dhungel R., Aiken R., Evett S. R., Colaizzi P. D., Marek G., Moorhead J. E., Baumhardt R. L., Brauer D., Kutikoff S., Lin X. Energy imbalance and evapotranspiration hysteresis under an advective environment: Evidence from lysimeter, eddy covariance, and energy balance modeling // Geophysical Research Letters. 2021. Vol. 48. No. 1. ID e2020GL091203. DOI: 10.1029/2020GL091203.
Diaconu D., Wassenberg M., Spiecker H. Variability of European beech wood density as influenced by interactions between tree-ring growth and aspect // Forest Ecosystems. 2016. Vol. 3. ID 6. DOI: 10.1186/s40663-016-0065-8.
Díaz‑Maroto I. J., Sylvain T. Analysis of physical properties of wood in three species of Galician oaks for the manufacture of wine barrels. Part I: Wood infradensity // Wood Research. 2016. Vol. 61. No. 5. P. 683–695.
Dickinson R. E. Modeling evapotranspiration for three‐dimensional global climate models // Climate Processes and Climate Sensitivity. 1984. Vol. 29. P. 58–72. DOI: 10.1029/GM029p0058.
Didion M., Frey B., Rogiers N., Thürig E. Validating tree litter decomposition in the Yasso07 carbon model // Ecological Modelling. 2014. Vol. 291. P. 58–68. DOI: 10.1016/j.ecolmodel.2014.07.028.
Dreyer E., Le Roux X., Montpied P., Daudet F. A., Masson F. Temperature response of leaf photosynthetic capacity in seedlings from seven temperate tree species // Tree Physiology. 2001. Vol. 21. No. 4. P. 223–232. DOI: 10.1093/treephys/21.4.223.
Dulamsuren C., Hauck M., Bader M., Osokhjargal D., Oyungerel S., Nyambayar S., Runge M., Leuschner C. Water relations and photosynthetic performance in Larix sibirica growing in the forest-steppe ecotone of Northern Mongolia // Tree Physiology. 2008. Vol. 29. No. 1. P. 99–110. DOI: 10.1093/treephys/tpn008.
Dulamsuren C., Hauck M., Bader M., Oyungerel S., Osokhjargal D., Nyambayar S., Leuschner C. The different strategies of Pinus sylvestris and Larix sibirica to deal with summer drought in a northern Mongolian forest–steppe ecotone suggest a future superiority of pine in a warming climate // Canadian Journal of Forest Research. 2009. Vol. 39. No. 12. P. 2520–2528. DOI: 10.1139/X09-156.
Ďurkovič J., Čaňová I., Priwitzer T., Biroščíková M., Kapral P., Saniga M. Field assessment of photosynthetic characteristics in micropropagated and grafted wych elm (Ulmus glabra Huds.) trees // Plant Cell, Tissue and Organ Culture (PCTOC). 2010. Vol. 101. P. 221–228. DOI: 10.1007/s11240-010-9680-1.
Èermák J. Leaf distribution in large trees and stands of the floodplain forest in southern Moravia // Tree Physiology. 1998. Vol. 18. No. 1. P. 727–737. DOI: 10.1093/treephys/18.11.727.
Elkie P. C., Rempel R. S. Detecting scales of pattern in boreal forest landscapes // Forest Ecology and Management. 2001. Vol. 147. No. 2–3. P. 253–261. DOI: 10.1016/S0378-1127(00)00467-9.
Evstigneev O. I. Ontogenetic scales of relation of trees to light (on the example of eastern European forests) // Russian Journal of Ecosystem Ecology. 2018. Vol. 3. No. 3. DOI: 10.21685/2500-0578-2018-3-3.
Evstigneev O. I., Korotkov V. N. Ontogenetic stages of trees: an overview // Russian Journal of Ecosystem Ecology. 2016. Vol. 1. No. 2. DOI: 10.21685/2500-0578-2016-2-1.
Fajardo A., Goodburn J. M., Graham J. Spatial patterns of regeneration in managed uneven-aged ponderosa pine/Douglas-fir forests of Western Montana, USA // Forest Ecology and Management. 2006. Vol. 223. No. 1. P. 255–266. DOI: 10.1016/j.foreco.2005.11.022.
Falster D. S., Duursma R. A., Ishihara M. I., Barneche D. R., FitzJohn R. G., …, & York R. A. BAAD: a Biomass And Allometry Database for woody plants // Ecology. 2015. Vol. 96. No. 5. P. 1445–1445. DOI: 10.1890/14-1889.1.
Finsterwalder S. Der suldenferner // Zeitschrift des Deutschen und Österreichischen Alpenvereins. 1887. V. 18. P. 72–89.
Fomin S. V. Generalized Robinson–Schensted–Knuth correspondence // Journal of Mathematical Sciences. 1988. Vol. 41. No. 2. P. 979–991. DOI: 10.1007/BF01247093.
Forrester D. I., Bauhus J. A review of processes behind diversity — Productivity relationships in forest // Current Forestry Reports. 2016. Vol. 2. P. 45–61. DOI: 10.1007/s40725-016-0031-2.
Forrester D. I., Tachauer I. H. H., Annighoefer P., Barbeito I., Pretzsch H., Ruiz‑Peinado R., Stark H., Vacchiano G., Zlatanov T., Chakraborty T., Saha S., Sileshi G. W. Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate // Forest Ecology and Management. 2017. Vol. 396. P. 160–175. DOI: 10.1016/j.foreco.2017.04.011.
Frank A. B., Liebig M. A., Hanson J. D. Soil carbon dioxide fluxes in northern semiarid grasslands // Soil Biology and Biochemistry. 2002. Vol. 34. No. 9. P. 1235–1241. DOI: 10.1016/S0038-0717(02)00062-7.
Friedlingstein P., Fung I., Holland E., John J., Brasseur G., Erickson D., Schimel D. On the contribution of CO2 fertilization to the missing biospheric sink // Global Biogeochemical Cycles. 1995. Vol. 9. No. 4. P. 541–556. DOI: 10.1029/95GB02381.
Frolov P., Shanin V., Zubkova E., Salemaa M., Mäkipää R., Grabarnik P. Predicting biomass of bilberry (Vaccinium myrtillus) using rank distribution and root-to-shoot ratio models // Plant Ecology. 2022. Vol. 223. No. 2. P. 131–140. DOI: 10.1007/s11258-021-01199-1.
Frolov P. V., Zubkova E. V., Komarov A. S. A cellular automata model for a community comprising two plant species of different growth forms // Biology Bulletin of the Russian Academy of Sciences. 2015. Vol. 42. P. 279–286. DOI: 10.1134/S1062359015040044.
Frolov P. V., Shanin V. N., Zubkova E. V., Bykhovets S. S., Grabarnik P. Y. CAMPUS‑S — The model of ground layer vegetation populations in forest ecosystems and their contribution to the dynamics of carbon and nitrogen. I. Problem formulation and description of the model // Ecological Modelling. 2020a. Vol. 431. ID 109184. DOI: 10.1016/j.ecolmodel.2020.109184.
Frolov P. V., Zubkova E. V., Shanin V. N., Bykhovets S. S., Mäkipää R., Salemaa M. CAMPUS‑S — The model of ground layer vegetation populations in forest ecosystems and their contribution to the dynamics of carbon and nitrogen // II. Parameterization, validation and simulation experiments. Ecological Modelling. 2020b. Vol. 431. ID 109183. DOI: 10.1016/j.ecolmodel.2020.109183.
Gale M. R., Grigal D. F. Vertical root distributions of northern tree species in relation to successional status // Canadian Journal of Forest Research. 1987. Vol. 17. No. 8. P. 829–834. DOI: 10.1139/x87-131.
Gardiner E. S., Löf M., O’Brien J. J., Stanturf J. A., Madsen P. Photosynthetic characteristics of Fagus sylvatica and Quercus robur established for stand conversion from Picea abies // Forest Ecology and Management. 2009. Vol. 258. No. 5. P. 868–878. DOI: 10.1016/j.foreco.2009.03.022.
Gebauer T. Water turnover in species-rich and species-poor deciduous forests: xylem sap flow and canopy transpiration: Dissertation. Biodiversity and Ecology Series B. Vol. 4. Göttingen: Georg-August-Universität, 2010. 146 p. DOI: 10.3249/webdoc-2324.
Gessler A., Schneider S., von Sengbusch D., Weber P., Hanemann U., Huber C., Rothe A., Kreutzer K., Rennenberg H. Field and laboratory experiments on net uptake of nitrate and ammonium by the roots of spruce (Picea abies) and beech (Fagus sylvatica) trees // New Phytologist. 1998. Vol. 138. No. 2. P. 275–285. DOI: 10.1046/j.1469-8137.1998.00107.x.
Geßler A., Keitel C., Kreuzwieser J., Matyssek R., Seiler W., Rennenberg H. Potential risks for European beech (Fagus sylvatica L.) in a changing climate // Trees. 2007. Vol. 21. No. 1. P. 1–11. DOI: 10.1007/s00468-006-0107-x.
Giagli K., Baar J., Fajstavr M., Gryc V., Vavrčík H. Tree-ring width and variation of wood density in Fraxinus excelsior L. and Quercus robur L. growing in floodplain forests // BioResources. 2018. Vol. 13. No. 1. P. 804–819. DOI: 10.15376/biores.13.1.804-819.
Giertych M. J., Karolewski P., Oleksyn J. Carbon allocation in seedlings of deciduous tree species depends on their shade tolerance // Acta Physiologiae Plantarum. 2015. Vol. 37. ID 216. DOI: 10.1007/s11738-015-1965-x.
Goisser M., Geppert U., Rötzer T., Paya A., Huber A., Kerner R., Bauerle T., Pretzsch H., Pritsch K., Häberle K. H., Matyssek R., Grams T. E. E. Does belowground interaction with Fagus sylvatica increase drought susceptibility of photosynthesis and stem growth in Picea abies? // Forest Ecology and Management. 2016. Vol. 375. P. 268–278. DOI: 10.1016/j.foreco.2016.05.032.
Goreaud F., Loreau M., Millier C. Spatial structure and the survival of an inferior competitor: a theoretical model of neighbourhood competition in plants // Ecological Modelling. 2002. Vol. 158. No. 1–2. P. 1–19. DOI: 10.1016/S0304-3800(02)00058-3.
Goulden M. L., Daube B. C., Fan S.‑M., Sutton D. J., Bazzaz A., Munger J. W., Wofsy S. C. Physiological response of a black spruce forest to weather // Journal of Geophysical Research: Atmospheres. 1997. Vol. 102. No. D24. P. 28987–28996. DOI: 10.1029/97JD01111.
Grime J. P. Plant strategies, vegetation processes, and ecosystem properties. 2nd edition. John Wiley & Son, 2002. 417 p.
Grossi G., Lendvai A., Peretti G., Ranzi R. Snow precipitation measured by gauges: Systematic error estimation and data series correction in the central Italian Alps // Water. 2017. Vol. 9. No. 7. ID 461. DOI: 10.3390/w9070461.
Gryc V., Vavrčík H., Gomola Š. Selected properties of European beech (Fagus sylvatica L.) // Journal of Forest Science. 2008. Vol. 54. No. 9. P. 418–425. DOI: 10.17221/59/2008-JFS.
Grygoruk D. Root vitality of Fagus sylvatica L., Quercus petraea Liebl. and Acer pseudoplatanus L. in mature mixed forest stand // Folia Forestalia Polonica. Series A — Forestry. 2016. Vol. 58. No. 2. P. 55–61. DOI: 10.1515/ffp-2016-0006.
Gspaltl M., Bauerle W., Binkley D., Sterba H. Leaf area and light use efficiency patterns of Norway spruce under different thinning regimes and age classes // Forest Ecology and Management. 2013. Vol. 288. P. 49–59. DOI: 10.1016/j.foreco.2011.11.044.
Guerrero‑Ramírez N. R., Mommer L., Freschet G. T., Iversen C. M., McCormack M. L., …, & Weigelt A. Global root traits (GRooT) database // Global Ecology and Biogeography. 2021. Vol. 30. No. 1. P. 25–37. DOI: 10.1111/geb.13179.
Gupta A. K. Beta distribution / International encyclopedia of statistical science. Lovric M. (ed.). Springer, 2011. P. 144–145. DOI: 10.1007/978-3-642-04898-2_144.
Haefner J. W., Poole G. C., Dunn P. V., Decker R. T. Edge effects in computer models of spatial competition // Ecological Modelling. 1991. Vol. 56. P. 221–244. DOI: 10.1016/0304-3800(91)90201-B.
Hagemeier M., Leuschner C. Functional crown architecture of five temperate broadleaf tree species: Vertical gradients in leaf morphology, leaf angle, and leaf area density // Forests. 2019a. Vol. 10. No. 3. ID 265. DOI: 10.3390/f10030265.
Hagemeier M., Leuschner C. Leaf and crown optical properties of five early-, mid- and late-successional temperate tree species and their relation to sapling light demand // Forests. 2019b. Vol. 10. No. 10. ID 925. DOI: 10.3390/f10100925.
Hamada J., Pétrissans A., Mothe F., Ruelle J., Pétrissans M., Gérardin P. Variations in the natural density of European oak wood affect thermal degradation during thermal modification // Annals of Forest Science. 2016. Vol. 73. No. 2. P. 277–286. DOI: 10.1007/s13595-015-0499-0.
Hanson P. J., Todd D. E., Amthor J. S. A six-year study of sapling and large-tree growth and mortality responses to natural and induced variability in precipitation and throughfall // Tree Physiology. 2001. Vol. 21. No. 6. P. 345–358. DOI: 10.1093/treephys/21.6.345.
Hansson K., Helmisaari H.‑S., Sah S. P., Lange H. Fine root production and turnover of tree and understorey vegetation in Scots pine, silver birch and Norway spruce stands in SW Sweden // Forest Ecology and Management. 2013. Vol. 309. P. 58–65. DOI: 10.1016/j.foreco.2013.01.022.
Hansson K., Kleja D. B., Kalbitz K., Larsson H. Amounts of carbon mineralised and leached as DOC during decomposition of Norway spruce needles and fine roots // Soil Biology and Biochemistry. 2010. Vol. 42. No. 2. P. 178–185. DOI: 10.1016/j.soilbio.2009.10.013.
Hättenschwiler S., Gasser P. Soil animals alter plant litter diversity effects on decomposition // Proceedings of the National Academy of Sciences. 2005. Vol. 102. No. 5. P. 1519–1524. DOI: 10.1073/pnas.0404977102.
Helmisaari H.‑S., Derome J., Nöjd P., Kukkola M. Fine root biomass in relation to site and stand characteristics in Norway spruce and Scots pine stands // Tree Physiology. 2007. Vol. 27. No. 10. P. 1493–1504. DOI: 10.1093/treephys/27.10.1493.
Helmisaari H.‑S., Makkonen K., Kellomäki S., Valtonen E., Mälkönen E. Below- and above-ground biomass, production and nitrogen use in Scots pine stands in eastern Finland // Forest Ecology and Management. 2002. Vol. 165. No. 1–3. P. 317–326. DOI: 10.1016/S0378-1127(01)00648-X.
Helmisaari H.-S., Sah S., Aro L. Fine roots on intensive forest ecosystem monitoring plots FIP4, FIP10 and FIP11 on Olkiluoto island in 2008. Working Report 2009-127. Finnish Forest Research Institute, 2009. 33 p.
Heräjärvi H., Junkkonen R. Wood density and growth rate of European and hybrid aspen in southern Finland // Baltic Forestry. 2006. Vol. 12. No. 1. P. 2–8.
Herben T., Wildová R. Community-level effects of plant traits in a grassland community examined by multispecies model of clonal plant growth // Ecological Modelling. 2012. Vol. 234. P. 60–69. DOI: 10.1016/j.ecolmodel.2011.06.012.
Hertel C., Leuchner M., Rötzer T., Menzel A. Assessing stand structure of beech and spruce from measured spectral radiation properties and modeled leaf biomass parameters // Agricultural and Forest Meteorology. 2012. Vol. 165. P. 82–91. DOI: 10.1016/j.agrformet.2012.06.008.
Hinckley T. M., Lassoie J. P., Running S. W. Temporal and spatial variations in the water status of forest trees // Forest Science. 1978. Vol. 24. Suppl. 1. P. a0001–z0001.
Hirvelä H., Härkönen K., Lempinen R., Salminen O. MELA2016 Reference Manual / Natural resources and bioeconomy studies 2017/7. Natural Resources Institute Finland, Helsinki, 2017. 547 p.
Hobbie S. E., Oleksyn J., Eissenstat D. M., Reich P. B. Fine root decomposition rates do not mirror those of leaf litter among temperate tree species // Oecologia. 2010. Vol. 162. No. 2. P. 505–513. DOI: 10.1007/s00442-009-1479-6.
Hristopulos D. T. Gaussian random fields / Random fields for spatial data modeling. Advances in geographic information science. Springer, 2020. P. 245–307. DOI: 10.1007/978-94-024-1918-4_6
Iivonen S., Kaakinen S., Jolkkonen A., Vapaavuori E., Linder S. Influence of long-term nutrient optimization on biomass, carbon, and nitrogen acquisition and allocation in Norway spruce // Canadian Journal of Forest Research. 2006. Vol. 36. No. 6. P. 1563–1571. DOI: 10.1139/x06-035.
IPCC: Climate Change 2013: The physical science basis. Contribution of Working Group I to the Fifth assessment report of the Intergovernmental Panel on Climate Change / Stocker T. F., Qin D., Plattner G.‑K., Tignor M., Allen S. K., Boschung J., Nauels A., Xia Y., Bex V., Midgley P. M. (eds.). Cambridge: Cambridge University Press, 2013. 1535 p.
Jagodzinski A. M., Ziółkowski J., Warnkowska A., Prais H. Tree age effects on fine root biomass and morphology over chronosequences of Fagus sylvatica, Quercus robur and Alnus glutinosa stands // PLoS ONE. 2016. Vol. 11. No. 2. ID e0148668. DOI: 10.1371/journal.pone.0148668.
Jacovides C. P., Boland J., Asimakopoulos D. N., Kaltsounides N. A. Comparing diffuse radiation models with one predictor for partitioning incident PAR radiation into its diffuse component in the eastern Mediterranean basin // Renewable Energy. 2010. Vol. 35. No. 8. P. 1820–1827. DOI: 10.1016/j.renene.2009.11.015.
Jaloviar P., Kucbel S., Vencurik J., Kýpeťová M., Parobeková Z., Pittner J., Saniga M., Sedmáková D. Underplanted silver fir and common beech cause changes in root stratification and morphology in mature spruce stands // Plant Root. 2018. Vol. 12. P. 21–30. DOI: 10.3117/plantroot.12.21.
Jarvis P. G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field // Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences. 1976. Vol. 273. No. 927. P. 593–610. DOI: 10.1098/rstb.1976.0035.
Jia Y., Yu G., Gao Y., He N., Wang Q., Jiao C., Zuo Y. Global inorganic nitrogen dry deposition inferred from ground- and space-based measurements // Nature Scientific Reports. 2016. Vol. 6. ID 19810. DOI: 10.1038/srep19810.
Jiao W., Wang W., Peng C., Lei X., Ruan H., Yang Y., Grabarnik P., Shanin V. Improving a process-based model to simulate forest carbon allocation under varied stand density // Forests. 2022. Vol. 13. No. 8. ID 1212. DOI: 10.3390/f13081212.
Jucker T., Fischer F. J., Chave J., Coomes D. A., Caspersen J., …, & Zavala M. A. Tallo: a global tree allometry and crown architecture database // Global Change Biology. 2022. Vol. 28. No. 17. P. 5254–5268. DOI: 10.1111/gcb.16302.
Juutinen A., Ahtikoski A., Mäkipää R., Shanin V. Effect of harvest interval and intensity on the profitability of uneven-aged management of Norway spruce stands // Forestry: An International Journal of Forest Research. 2018. Vol. 91. No. 5. P. 589–602. DOI: 10.1093/forestry/cpy018.
Jyske T., Mäkinen H., Saranpää P. Wood density within Norway spruce stems // Silva Fennica. 2008. Vol. 42. No. 3. P. 439–455. DOI: 10.14214/sf.248.
Kajimoto T., Matsuura Y., Sofroтov M. A., Volokitina A. V., Mori S., Osawa A., Abaimov A. P. Above- and belowground biomass and net primary productivity of a Larix gmelinii stand near Tura, central Siberia // Tree Physiology. 1999. Vol. 19. No. 12. P. 815–822. DOI: 10.1093/treephys/19.12.815.
Kalela E. K. Männiköiden ja kuusikoiden juurisuhteista I (On the horizontal roots in pine and spruce stand I) // Silva Fennica (Acta Forestalia Fennica). 1949. Vol. 57. No. 2. ID 7398. DOI: 10.14214/aff.7398.
Kalela E. K. Mäntysiemenpuiden ja -puustojen juurisuhteista // Silva Fennica (Acta Forestalia Fennica). 1954. Vol. 61. No. 28. ID 7440. DOI: 10.14214/aff.7440.
Kalliokoski T. Root system traits of Norway spruce, Scots pine, and silver birch in mixed boreal forests: an analysis of root architecture, morphology, and anatomy: Dissertation. Dissertationes Forestales. 2011. Vol. 121. 67 p.
Kalliokoski T., Nygren P., Sievänen R. Coarse root architecture of three boreal tree species growing in mixed stands // Silva Fennica. 2008. Vol. 42. No. 2. P. 189–210. DOI: 10.14214/sf.252.
Kalliokoski T., Pennanen T., Nygren P., Sievänen R., Helmisaari H.‑S. Belowground interspecific competition in mixed boreal forests: fine root and ectomycorrhiza characteristics along stand developmental stage and soil fertility gradients // Plant and Soil. 2010a. Vol. 330. P. 73–89. DOI: 10.1007/s11104-009-0177-9.
Kalliokoski T., Sievänen R., Nygren P. Tree roots as self-similar branching structures: axis differentiation and segment tapering in coarse roots of three boreal forest tree species // Trees. 2010b. Vol. 24. P. 219–236. DOI: 10.1007/s00468-009-0393-1.
Kang S., Kim S., Oh S., Lee D. Predicting spatial and temporal patterns of soil temperature based on topography, surface cover and air temperature // Forest Ecology and Management. 2000. Vol. 136. No. 1–3. P. 173–184. DOI: 10.1016/S0378-1127(99)00290-X.
Kärki T. Variation of wood density and shrinkage in European aspen (Populus tremula) // Holz als Roh- und Werkstoff. 2001. Vol. 59. No. 1–2. P. 79–84. DOI: 10.1007/s001070050479.
Kätterer T., Reichstein M., Andrén O., Lomander A. Temperature dependence of organic matter decomposition: a critical review using literature data analyzed with different models // Biology and fertility of soils. 1998. Vol. 27. No. 3. P. 258–262. DOI: 10.1007/s003740050430.
Kazda M., Salzer J., Reiter I. Photosynthetic capacity in relation to nitrogen in the canopy of a Quercus robur, Fraxinus angustifolia and Tilia cordata flood plain forest // Tree Physiology. 2000. Vol. 20. No. 15. P. 1029–1037. DOI: 10.1093/treephys/20.15.1029.
Kellomäki S., Väisänen H., Strandman H. FinnFor: a model for calculating the response of the boreal forest ecosystem to climate changes / Research Note. No. 6. Faculty of Forestry, University of Joensuu, Finland, 1993. 120 p.
Kelty M. J. The role of species mixtures in plantation forestry // Forest Ecology and Management. 2006. Vol. 233. No. 2–3. P. 195–204. DOI: 10.1016/j.foreco.2006.05.011.
Kharuk V. I., Im S. T., Petrov I. A., Dvinskaya M. L., Fedotova E. V., Ranson K. J. Fir decline and mortality in the southern Siberian Mountains // Regional Environmental Change. 2017. Vol. 17. No. 3. P. 803–812. DOI: 10.1007/s10113-016-1073-5.
Kiaei M., Samariha A. Wood density and shrinkage of Ulmus glabra in Northwestern of Iran // American-Eurasian Journal of Agricultural & Environmental Sciences. 2011. Vol. 11. No. 2. P. 257–260.
Kloeppel B. D., Abrams M. D. Ecophysiological attributes of the native Acer saccharum and the exotic Acer platanoides in urban oak forests in Pennsylvania, USA // Tree Physiology. 1995. Vol. 15. No. 11. P. 739–746. DOI: 10.1093/treephys/15.11.739.
Köcher P., Gebauer T., Horna V., Leuschner C. Leaf water status and stem xylem flux in relation to soil drought in five temperate broad-leaved tree species with contrasting water use strategies // Annals of Forest Science. 2009. Vol. 66. No. 1. ID 101. DOI: 10.1051/forest/2008076.
Kolari P., Pumpanen J., Kulmala L., Ilvesniemi H., Nikinmaa E., Grönholm T., Hari P. Forest floor vegetation plays an important role in photosynthetic production of boreal forests // Forest Ecology and Management. 2006. Vol. 221. No. 1–3. P. 241–248. DOI: 10.1016/j.foreco.2005.10.021.
Kolobov A. N., Frisman E. Y. Evaluate the initial spatial structure and heterogeneity of the composition for spruce and larch stands on real data self-thinning of even-aged stands // Ecological Complexity. 2018. Vol. 34. P. 89–99. DOI: 10.1016/j.ecocom.2017.09.005.
Komarov A., Chertov O., Bykhovets S., Shaw C., Nadporozhskaya M., Frolov P., Shashkov M., Shanin V., Grabarnik P., Priputina I., Zubkova E. Romul_Hum model of soil organic matter formation coupled with soil biota activity. I. Problem formulation, model description, and testing // Ecological Modelling. 2017a. Vol. 345. P. 113–124. DOI: 10.1016/j.ecolmodel.2016.08.007.
Komarov A. S., Chertov O. G., Zudin S. L., Nadporozhskaya M. A., Mikhailov A. V., Bykhovets S. S., Zudina E. V., Zoubkova E. V. EFIMOD 2 — the system of simulation models of forest growth and elements cycles in forest ecosystems // Ecological Modelling. 2003a. Vol. 170. No. 2–3. P. 373–392. DOI: 10.1016/S0304-3800(03)00240-0.
Komarov A. S., Ginzhul L. K., Shanin V. N., Bykhovets S. S., Bobkova K. S., Kuznetsov M. A., Manov A. V., Osipov A. F. Pattern of biomass partitioning into fractions of boreal trees // Biology Bulletin of the Russian Academy of Sciences. 2017b. Vol. 44. No. 6. P. 626–633. DOI: 10.1134/S1062359017060061.
Komarov A. S., Khoraskina Y. S., Bykhovets S. S., Bezrukova M. G. Modelling of soil organic matter and elements of soil nutrition dynamics in mineral and organic forest soils: the ROMUL model expansion // Procedia Environmental Sciences. 2012. Vol. 13. P. 525–534. DOI: 10.1016/j.proenv.2012.01.043.
Komarov A. S., Palenova M. M., Smirnova O. V. The concept of discrete description of plant ontogenesis and cellular automata models of plant populations // Ecological Modeling. 2003b. Vol. 170. No. 2. P. 427–439. DOI: 10.1016/S0304-3800(03)00243-6.
Komarov A. S., Shanin V. N. Comparative analysis of the influence of climate change and nitrogen deposition on carbon sequestration in forest ecosystems in European Russia: simulation modelling approach // Biogeosciences. 2012. Vol. 9. No. 11. P. 4757–4770. DOI: 10.5194/bg-9-4757-2012.
Korzukhin M. D., Ter-Mikaelian M. T. An individual-tree-based model of competition for light // Ecological Modelling. 1995. Vol. 79. No. 1–3. P. 221–229. DOI: 10.1016/0304-3800(94)00039-K.
Koshurnikova N., Makhnykina A., Garmash A., Zlenko L., Verkhovets S. Production of phytomass carbon in the dark coniferous forest of the Western Siberia // 18th International Multidisciplinary Scientific Geoconference SGEM 2018 (2–8 July 2018, Albena, Bulgaria). Conference Proceedings. Vol. 18. P. 885–892. DOI: 10.5593/sgem2018/3.2.
Kuehne C., Kublin E., Pyttel P., Bauhus J. Growth and form of Quercus robur and Fraxinus excelsior respond distinctly different to initial growing space: results from 24-year-old Nelder experiments // Journal of Forestry Research. 2013. Vol. 24. P. 1–14. DOI: 10.1007/s11676-013-0320-6.
Kükenbrink D., Gardi O., Morsdorf F., Thürig E., Schellenberger A., Mathys L. Above-ground biomass references for urban trees from terrestrial laser scanning data // Annals of Botany. 2021. Vol. 128. No. 6. P. 709–724. DOI: 10.1093/aob/mcab002.
Kulha N., Pasanen L., Holmström L., De Grandpré L., Kuuluvainen T., Aakala T. At what scales and why does forest structure vary in naturally dynamic boreal forests? An analysis of forest landscapes on two continents // Ecosystems. 2018. Vol. 22. P. 709–724. DOI: 10.1007/s10021-018-0297-2.
Kull O., Koppel A. Net photosynthetic response to light intensity of shoots from different crown positions and age in Picea abies (L.) Karst. // Scandinavian Journal of Forest Research. 1987. Vol. 2. No. 1–4. P. 157–166. DOI: 10.1080/02827588709382454.
Kutikoff S., Lin X., Evett S. R., Gowda P., Brauer D., Moorhead J., Marek G., Colaizzi P., Aiken R., Xu L., Owensby C. Water vapor density and turbulent fluxes from three generations of infrared gas analyzers // Atmospheric Measurement Techniques. 2021. Vol. 14. No. 2. P. 1253–1266. DOI: 10.5194/amt-14-1253-2021.
Kuuluvainen T., Hokkanen T. J., Järvinen E., Pukkala T. Factors related to seedling growth in a boreal Scots pine stand: a spatial analysis of a vegetation-soil system // Canadian Journal of Forest Research. 1993. Vol. 23. No. 10. P. 2101–2109. DOI: 10.1139/x93-262.
Kuuluvainen T., Syrjänen K., Kalliola R. Structure of a pristine Picea abies forest in northeastern Europe // Journal of Vegetation Science. 1998. Vol. 9. No. 4. P. 563–574. DOI: 10.2307/3237272.
Kuzyakova I. F., Kuzyakov Y. V., Thomas E. Wirkung des Mikroreliefs auf die räumliche Variabilität des Kohlenstoffgehaltes eines Podzoluvisols in einem Dauerdüngungsversuch (Effect of microrelief on the spatial variability of carbon content of a Podzoluvisol in a long term field trial) // Zeitschrift fur Pflanzenernahrung und Bodenkunde. 1997. Vol. 160. No. 5. P. 555–561. DOI: 10.1002/jpln.19971600506.
Laitakari E. Männyn juuristo. Morfologinen tutkimus (The root system of pine [Pinus sylvestris]: a morphological investigation) // Silva Fennica (Acta Forestalia Fennica). 1927. Vol. 33. No. 1. ID 7210. DOI: 10.14214/aff.7210.
Laitakari E. Koivun juuristo (The root system of birch [Betula verrucosa and odorata]) // Silva Fennica (Acta Forestalia Fennica). 1934. Vol. 41. No. 2. ID 7315. DOI: 10.14214/aff.7315.
Lal R., Suleimenov M., Stewart B. A., Hansen D. O., Doraiswamy P. Climate change and terrestrial carbon sequestration in Central Asia. CRC Press, 2007. 512 p. DOI: 10.1201/9780203932698.
Landsberg J. J., Waring R. H. A generalised model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning // Forest Ecology and Management. 1997. Vol. 95. No. 3. P. 209–228. DOI: 10.1016/S0378-1127(97)00026-1.
Lasch‑Born P., Suckow F., Reyer C. P. O., Gutsch M., Kollas C., Badeck F.-W., Bugmann H. K. M., Grote R., Fürstenau F., Lindner M., Schaber J. Description and evaluation of the process-based forest model 4C v2.2 at four European forest sites // Geoscientific Model Development. 2020. Vol. 13. No. 11. P. 5311–5343. DOI: 10.5194/gmd-13-5311-2020.
Law B. E., Baldocchi D. D., Anthoni P. M. Below-canopy and soil CO2 fluxes in a ponderosa pine forest // Agricultural and Forest Meteorology. 1999. Vol. 94. No. 3–4. P. 171–188. DOI: 10.1016/S0168-1923(99)00019-2.
Le Goff N., Granier A., Ottorini J.‑M., Peiffer M. Biomass increment and carbon balance of ash (Fraxinus excelsior) trees in an experimental stand in northeastern France // Annals of Forest Science. 2004. Vol. 61. No. 6. P. 577–588. DOI: 10.1051/forest:2004053.
Lehmann J., Kleber M. The contentious nature of soil organic matter // Nature. 2015. Vol. 528. P. 60–68. DOI: 10.1038/nature16069.
Lemoine D., Peltier J.‑P., Marigo G. Comparative studies of the water relations and the hydraulic characteristics in Fraxinus excelsior, Acer pseudoplatanus and A. opalus trees under soil water contrasted conditions // Annals of Forest Science. 2001. Vol. 58. No. 7. P. 723–731. DOI: 10.1051/forest:2001159.
Leuschner C., Hagemeier M. The economy of canopy space occupation and shade production in early- to late-successional temperate tree species and their relation to productivity // Forests. 2020. Vol. 11. No. 3. ID 317. DOI: 10.3390/f11030317.
Leuschner C., Hertel D., Schmid I., Koch O., Muhs A., Hölscher D. Stand fine root biomass and fine root morphology in old-growth beech forests as a function of precipitation and soil fertility // Plant and Soil. 2004. Vol. 258. P. 43–56. DOI: 10.1023/B:PLSO.0000016508.20173.80.
Levin S. A. The problem of pattern and scale in ecology: the Robert H. MacArthur award lecture // Ecology. 1992. Vol. 73. No. 6. P. 1943–1967. DOI: 10.2307/1941447.
Lexer M. J., Hönninger K. A modified 3D‑patch model for spatially explicit simulation of vegetation composition in heterogeneous landscapes // Forest Ecology and Management. 2001. Vol. 144. No. 1–3. P. 43–65. DOI: 10.1016/S0378-1127(00)00386-8.
Liang W. L., Uchida T. Effects of topography and soil depth on saturated-zone dynamics in steep hillslopes explored using the three-dimensional Richards’ equation // Journal of Hydrology. 2014. Vol. 510. P. 124–136. DOI: 10.1016/j.jhydrol.2013.12.029.
Liepiņš J., Ivanovs J., Lazdiņš A., Jansons J., Liepiņš K. Mapping of basic density within European aspen stems in Latvia // Silva Fennica. 2017. Vol. 51. No. 5. ID 7798. DOI: 10.14214/sf.7798.
Lintunen A. Crown architecture and its role in species interactions in mixed boreal forests: Dissertation. Dissertationes Forestales. Vol. 165. University of Helsinki, Faculty of Agriculture and Forestry, Department of Forest Sciences, 2013. 55 p.
Lintunen A., Kaitaniemi P. Responses of crown architecture in Betula pendula to competition are dependent on the species of neighbouring trees // Trees. 2010. Vol. 24. P. 411–424. DOI: 10.1007/s00468-010-0409-x.
Lintunen A., Sievänen R., Kaitaniemi P., Perttunen J. Models of 3D crown structure for Scots pine (Pinus sylvestris) and silver birch (Betula pendula) grown in mixed forest // Canadian Journal of Forest Research. 2011. Vol. 41. No. 9. P. 1779–1794. DOI: 10.1139/x11-092.
Loreau M. Separating sampling and other effects in biodiversity experiments // Oikos. 1998. Vol. 82. No. 3. P. 600–602. DOI: 10.2307/3546381.
Lukina N. V., Orlova M. A., Tikhonova E. V., Tebenkova D. N., Kazakova A. I., Gornov A. V., Smirnov V. E., Knyazeva S. V., Bakhmet O. N., Kryshen A. M., Shashkov M. P., Ershov V. V. The influence of vegetation on the forest soil properties in the republic of Karelia // Eurasian Soil Science. 2019. Vol. 52. No. 7. P. 793–807. DOI: 10.1134/S1064229319050077.
Lundegårdh H. Carbon dioxide evolution of soil and crop growth // Soil science. 1927. Vol. 23. No. 6. P. 417–453. DOI: 10.1097/00010694-192706000-00001.
Luoma S. Geographical pattern in photosynthetic light response of Pinus sylvestris in Europe // Functional Ecology. 1997. Vol. 11. No. 3. P. 273–281. DOI: 10.1046/j.1365-2435.1997.00089.x
Luostarinen K. Tracheid wall thickness and lumen diameter in different axial and radial locations in cultivated Larix sibirica trunks // Silva Fennica. 2012. Vol. 46. No. 5. P. 707–716. DOI: 10.14214/sf.921.
Luostarinen K., Verkasalo E. Birch as sawn timber and in mechanical further processing in Finland. A literature study / Silva Fennica Monographs 1, 2000. 40 p.
Luyssaert S., Schulze E. D., Börner A., Knohl A., Hessenmöller D., Law B. E., Ciais P., Grace J. Old-growth forests as global carbon sinks // Nature. 2008. Vol. 455. P. 213–215. DOI: 10.1038/nature07276.
Majdi H., Persson H. Spatial distribution of fine roots, rhizosphere and bulk-soil chemistry in an acidified Picea abies stand // Scandinavian Journal of Forest Research. 1993. Vol. 8. No. 1–4. P. 147–155. DOI: 10.1080/02827589309382764.
Mäkelä A., Hari P., Berninger F., Hänninen H., Nikinmaa E. Acclimation of photosynthetic capacity in Scots pine to the annual cycle of temperature // Tree Physiology. 2004. Vol. 24. No. 4. P. 369–376. DOI: 10.1093/treephys/24.4.369.
Mäkelä A., Pulkkinen M., Kolari P., Lagergren F., Berbigier P., Lindroth A., Loustau D., Nikinmaa E., Vesala T., Hari P. Developing an empirical model of stand GPP with the LUE approach: analysis of eddy covariance data at five contrasting conifer sites in Europe // Global Change Biology. 2008. Vol. 14. No. 1. P. 92–108. DOI: 10.1111/j.1365-2486.2007.01463.x.
Mäkelä A., Vanninen P. Vertical structure of Scots pine crowns in different age and size classes // Trees. 2001. Vol. 15. P. 385–392. DOI: 10.1007/s004680100118.
Mäkinen H., Saranpää P., Linder S. Wood-density variation of Norway spruce in relation to nutrient optimization and fibre dimensions // Canadian Journal of Forest Research. 2002. Vol. 32. No. 2. P. 185–194. DOI: 10.1139/x01-186.
Mao Z., Saint‑André L., Bourrier F., Stokes A., Cordonnier T. Modelling and predicting the spatial distribution of tree root density in heterogeneous forest ecosystems // Annals of Botany. 2015. Vol. 116. No. 2. P. 261–277. DOI: 10.1093/aob/mcv092.
Martens S. N., Breshears D. D., Meyer C. W. Spatial distribution of understory light along the grassland/forest continuum: effects of cover, height, and spatial patterns of tree canopies // Ecological Modelling. 2000. Vol. 126. No. 1. P. 79–93. DOI: 10.1016/S0304-3800(99)00188-X.
Matsinos Y. G., Troumbis A. Y. Modeling competition, dispersal and effects of disturbance in the dynamics of a grassland community using a cellular automaton model // Ecological Modelling. 2002. Vol. 149. No. 1–2. P. 71–83. DOI: 10.1016/S0304-3800(01)00515-4.
Mauer O., Houšková K., Mikita T. The root system of pedunculate oak (Quercus robur L.) at the margins of regenerated stands // Journal of Forest Science. 2017. Vol. 63. No. 1. P. 22–33. DOI: 10.17221/85/2016-JFS.
McCarthy J. Gap dynamics of forest trees: A review with particular attention to boreal forests // Environmental Reviews. 2001. Vol. 9. No. 1. P. 1–59. DOI: 10.1139/a00-012.
Mederski P. S., Bembenek M., Karaszewski Z., Giefing D. F., Sulima‑Olejniczak E., Rosińska M., Łacka A. Density and mechanical properties of Scots pine (Pinus sylvestris L.) wood from a seedling seed orchard // Drewno. 2015. Vol. 58. No. 195. P. 117–124. DOI: 10.12841/wood.1644-3985.123.10.
Medlyn B. E., Dreyer E., Ellsworth D., Forstreuter M., Harley P. C., Kirschbaum M. U. F., Le Roux X., Montpied P., Strassemeyer J., Walcroft A., Wang K., Loustau D. Temperature response of parameters of a biochemically based model of photosynthesis. II. A review of experimental data // Plant, Cell & Environment. 2002. Vol. 25. No. 9. P. 1167–1179. DOI: 10.1046/j.1365-3040.2002.00891.x.
Meier I. C., Knutzen F., Eder L. M., Müller‑Haubold H., Goebel M.‑O., Bachmann J., Hertel D., Leuschner C. The deep root system of Fagus sylvatica on sandy soil: Structure and variation across a precipitation gradient // Ecosystems. 2018. Vol. 21. P. 280–296. DOI: 10.1007/s10021-017-0148-6.
Meinen C., Hertel D., Leuschner C. Biomass and morphology of fine roots in temperate broad-leaved forests differing in tree species diversity: Is there evidence of below-ground overyielding? // Oecologia. 2009. Vol. 161. P. 99–111. DOI: 10.1007/s00442-009-1352-7.
Mihalakakou G., Santamouris M., Lewis J. O., Asimakopoulos D. N. On the application of the energy balance equation to predict ground temperature profiles // Solar Energy. 1997. Vol. 60. No. 3–4. P. 181–190. DOI: 10.1016/S0038-092X(97)00012-1.
Miner G. L., Bauerle W. L., Baldocchi D. D. Estimating the sensitivity of stomatal conductance to photosynthesis: a review // Plant, Cell and Environment. 2017. Vol. 40. No. 7. P. 1214–1238. DOI: 10.1111/pce.12871.
Moeur M. Spatial models of competition and gap dynamics in old-growth Tsuga heterophylla/Thuja plicata forests // Forest Ecology and Management. 1997. Vol. 94. No. 1. P. 175–186. DOI: 10.1016/S0378-1127(96)03976-X.
Moghaddam E. R. Growth, development and yield in pure and mixed forest stands // International Journal of Advanced Biological and Biomedical Research. 2014. Vol. 2. No. 10. P. 2725–2730.
Montesano P. M., Rosette J., Sun G., North P., Nelson R. F., Dubayah R. O., Ranson K. J., Kharuk V. The uncertainty of biomass estimates from modeled ICESat-2 returns across a boreal forest gradient // Remote Sensing of Environment. 2015. Vol. 158. P. 95–109. DOI: 10.1016/j.rse.2014.10.029.
Mõttus M., Ross J., Sulev M. Experimental study of ratio of PAR to direct integral solar radiation under cloudless conditions // Agricultural and Forest Meteorology. 2001. Vol. 109. No. 3. P. 161–170. DOI: 10.1016/S0168-1923(01)00269-6.
Mõttus M., Sulev M., Baret F., Lopez‑Lozano R., Reinart A. Photosynthetically active radiation: measurement and modeling / Solar Radiation. Richter C., Lincot D., Gueymard C. A. (Eds.). New York: Springer, 2013. P. 140–169.
Nabuurs G. J., Schelhaas M. J., Pussinen A. Validation of the European Forest Information Scenario Model (EFISCEN) and a projection of Finnish forests // Silva Fennica. 2000. Vol. 34. No. 2. P. 167–179. DOI: 10.14214/sf.638.
Nahm M., Matzarakis A., Rennenberg H., Geßler A. Seasonal courses of key parameters of nitrogen, carbon and water balance in European beech (Fagus sylvatica L.) grown on four different study sites along a European North–South climate gradient during the 2003 drought // Trees. 2007. Vol. 21. P. 79–92. DOI: 10.1007/s00468-006-0098-7.
Niinemets Ü. Changes in foliage distribution with relative irradiance and tree size: Differences between the saplings of Acer platanoides and Quercus robur // Ecological Research. 1996. Vol. 11. No. 3. P. 269–281. DOI: 10.1007/BF02347784.
Niinemets Ü. Growth of young trees of Acer platanoides and Quercus robur along a gap- understory continuum: Interrelationships between allometry, biomass partitioning, nitrogen, and shade tolerance // International Journal of Plant Sciences. 1998. Vol. 159. No. 2. P. 318–330. DOI: 10.1086/297553.
Niinemets Ü., Kull O. Stoichiometry of foliar carbon constituents varies along light gradients in temperate woody canopies: Implications for foliage morphological plasticity // Tree Physiology. 1998. Vol. 18. No. 7. P. 467–479. DOI: 10.1093/treephys/18.7.467.
Niinemets Ü., Oja V., Kull O. Shape of leaf photosynthetic electron transport versus temperature response curve is not constant along canopy light gradients in temperate deciduous trees // Plant, Cell & Environment. 1999. Vol. 22. No. 12. P. 1497–1513. DOI: 10.1046/j.1365-3040.1999.00510.x.
Niinemets Ü., Valladares F. Tolerance to shade, drought, and waterlogging of temperate Northern hemisphere trees and shrubs // Ecological Monographs. 2006. Vol. 76. No. 4. P. 521–547. DOI: 10.1890/0012-9615(2006)076[0521:TTSDAW]2.0.CO;2.
Nilsson M.-C., Wardle D. A. Understory vegetation as a forest ecosystem driver: evidence from the northern Swedish boreal forest // Frontiers in Ecology and the Environment. 2005. Vol. 3. No. 8. P. 421–428. DOI: 10.1890/1540-9295(2005)003[0421:UVAAFE]2.0.CO;2.
Nobel P. S., Geller G. N. Temperature modelling of wet and dry desert soils // The Journal of Ecology. 1987. Vol. 75. No. 1. P. 247–258. DOI: 10.2307/2260549.
Norby R. J., DeLucia E. H., Gielen B., Calfapietra C., Giardina C. P., King J. S., Ledford J., McCarthy H. R., Moore D. J. P., Ceulemans R., De Angelis P., Finzi A. C., Karnosky D. F., Kubiske M. E., Lukac M., Pregitzer K. S., Scarascia‑Mugnozza G. E., Schlesinger W. H., Oren R. Forest response to elevated CO2 is conserved across a broad range of productivity // Proceedings of the National Academy of Sciences. 2005. Vol. 102. No. 50. P. 18052–18056. DOI: 10.1073/pnas.0509478102.
Oborny B., Mony C., Herben T. From virtual plants to real communities: a review of modelling clonal growth // Ecological Modelling. 2012. Vol. 234. P. 3–19. DOI: 10.1016/j.ecolmodel.2012.03.010.
Olchev A., Radler K., Sogachev A., Panferov O., Gravenhorst G. Application of a three-dimensional model for assessing effects of small clear-cuttings on radiation and soil temperature // Ecological Modelling. 2009. Vol. 220. No. 21. P. 3046–3056. DOI: 10.1016/j.ecolmodel.2009.02.004.
Oleksyn J., Żytkowiak R., Reich P. B., Tjoelker M. G., Karolewski P. Ontogenetic patterns of leaf CO2 exchange, morphology and chemistry in Betula pendula trees // Trees. 2000. Vol. 14. P. 271–281. DOI: 10.1007/PL00009768.
Oostra S., Majdi H., Olsson M. Impact of tree species on soil carbon stocks and soil acidity in southern Sweden // Scandinavian Journal of Forest Research. 2006. Vol. 21. No. 5. P. 364–371. DOI: 10.1080/02827580600950172.
Ostonen I., Lõhmus K., Helmisaari H.‑S., Truu J., Meel S. Fine root morphological adaptations in Scots pine, Norway spruce and silver birch along a latitudinal gradient in boreal forests // Tree Physiology. 2007. Vol. 27. No. 11. P. 1627–1634. DOI: 10.1093/treephys/27.11.1627.
Oulehle F., Cosby B. J., Wright R. F., Hruška J., Kapáček J., Krám P., Evans C. D., Moldan F. Modelling soil nitrogen: the MAGIC model with nitrogen retention linked to carbon turnover using decomposer dynamics // Environmental Pollution. 2012. Vol. 165. P. 158–166. DOI: 10.1016/j.envpol.2012.02.021.
Pace R., De Fino F., Rahman M. A., Pauleit S., Nowak D. J., Grote R. A single tree model to consistently simulate cooling, shading, and pollution uptake of urban trees // International Journal of Biometeorology. 2021. Vol. 65. No. 2. P. 277–289. DOI: 10.1007/s00484-020-02030-8.
Packham J. R., Thomas P. A., Atkinson M. D., Degen T. Biological flora of the British Isles: Fagus sylvatica // Journal of Ecology. 2012. Vol. 100. P. 1557–1608. DOI: 10.1111/j.1365-2745.2012.02017.x.
Pagès L., Doussan C., Vercambre G. An introduction on below-ground environment and resource acquisition, with special reference on trees. Simulation models should include plant structure and function // Annals of Fores Science. 2000. Vol. 57. No. 5–6. P. 513–520. DOI: 10.1051/forest:2000138.
Pahaut E. Les cristaux de neige et leurs métamorphoses (Snow crystals and their metamorphosies) / Monographies de la Météorologie Nationale 96, 1975. 61 p.
Parajuli A., Nadeau D. F., Anctil F., Parent A. C., Bouchard B., Girard M., Jutras S. Exploring the spatiotemporal variability of the snow water equivalent in a small boreal forest catchment through observation and modeling // Hydrological Processes. 2020. Vol. 34. No. 11. P. 2628–2644. DOI: 10.1002/hyp.13756.
Parton W. J., Stewart J. W. B., Cole C. V. Dynamics of C, N, P and S in grasslands soils: a model // Biogeochemistry. 1988. Vol. 5. P. 109–131. DOI: 10.1007/BF02180320.
Peichl M., Leava N. A., Kiely G. Above- and belowground ecosystem biomass, carbon and nitrogen allocation in recently afforested grassland and adjacent intensively managed grassland // Plant and Soil. 2012. Vol. 350. P. 281–296. DOI: 10.1007/s11104-011-0905-9.
Pellicciotti F., Brock B., Strasser U., Burlando P., Funk M., Corripio J. An enhanced temperature-index glacier melt model including the shortwave radiation balance: development and testing for Haut Glacier d’Arolla, Switzerland // Journal of Glaciology. 2005. Vol. 51. No. 175. P. 573–587. DOI: 10.3189/172756505781829124.
Peng C., Liu J., Dang Q., Apps M. J., Jiang H. TRIPLEX: a generic hybrid model for predicting forest growth and carbon and nitrogen dynamic // Ecological Modelling. 2002. Vol. 153. No. 1–2. P. 109–130. DOI: 10.1016/S0304-3800(01)00505-1.
Peñuelas J., Estiarte M. Trends in plant carbon concentration and plant demand for N throughout this century // Oecologia. 1996. Vol. 109. P. 69–73. DOI: 10.1007/s004420050059.
Persson H., von Fircks Y., Majdi H., Nilsson L. O. Root distribution in a Norway spruce (Picea abies (L.) Karst.) stand subjected to drought and ammonium-sulphate application // Plant and Soil. 1995. Vol. 168. P. 161–165. DOI: 10.1007/BF00029324.
Perttunen J. The LIGNUM functional-structural tree model: Dissertation. Systems Analysis Laboratory, Helsinki University of Technology, 2009. 52 p.
Petriţan A. M., von Lüpke B., Petriţan I. C. Influence of light availability on growth, leaf morphology and plant architecture of beech (Fagus sylvatica L.), maple (Acer pseudoplatanus L.) and ash (Fraxinus excelsior L.) saplings // European Journal of Forest Research. 2009. Vol. 128. P. 61–74. DOI: 10.1007/s10342-008-0239-1.
Peuke A. D., Rennenberg H. Carbon, nitrogen, phosphorus, and sulphur concentration and partitioning in beech ecotypes (Fagus sylvatica L.): Phosphorus most affected by drought // Trees. 2004. Vol. 18. No. 6. P. 639–648. DOI: 10.1007/s00468-004-0335-x.
Pigott C. D. Tilia cordata Miller // Journal of Ecology. 1991. Vol. 79. No. 4. P. 1147–1207. DOI: 10.2307/2261105.
Plauborg F. Simple model for 10 cm soil temperature in different soils with short grass // European Journal of Agronomy. 2002. Vol. 17. No. 3. P. 173–179. DOI: 10.1016/S1161-0301(02)00006-0.
Pommerening A., Grabarnik P. Individual-based methods in forest ecology and management. Springer, 2019. 411 p. DOI: 10.1007/978-3-030-24528-3.
Posch M., Reinds G. J. A very simple dynamic soil acidification model for scenario analyses and target loads calculation // Environmental Modelling and Software. 2009. Vol. 24. No. 3. P. 329–340. DOI: 10.1016/j.envsoft.2008.09.007.
Praciak A. The CABI encyclopedia of forest trees. CABI, 2013. 536 p.
Prentice I. C., Helmisaari H. Silvics of North European trees: Compilation, comparisons and implications for forest succession modelling // Forest Ecology and Management. 1991. Vol. 42. No. 1–2. P. 79–93. DOI: 10.1016/0378-1127(91)90066-5.
Pretzsch H. Canopy space filling and tree crown morphology in mixed-species stands // Forest Ecology and Management. 2014. Vol. 327. P. 251–264. DOI: 10.1016/j.foreco.2014.04.027.
Pretzsch H. The effect of tree crown allometry on community dynamics in mixed-species stands versus monocultures. A review and perspectives for modeling and silvicultural regulation // Forests. 2019. Vol. 10. No. 9. ID 810. DOI: 10.3390/f10090810.
Pretzsch H., Biber P., Ďurský J. The single tree-based stand simulator SILVA: Construction, application and evaluation // Forest Ecology and Management. 2002. Vol. 162. No. 1. P. 3–21. DOI: 10.1016/S0378-1127(02)00047-6.
Pretzsch P., Biber P., Uhl E., Dahlhausen J., Rötzer T., Caldentey J., Koike T., van Con T., Chavanne A., Seifert T., du Toit B., Farnden C., Pauleit S. Crown size and growing space requirement of common tree species in urban centres, parks, and forests // Urban Forestry & Urban Greening. 2015. Vol. 14. No. 3. P. 466–479. DOI: 10.1016/j.ufug.2015.04.006.
Pretzsch H., Bielak K., Block J., Bruchwald A., Dieler J., Ehrhart H.‑P., Kohnle U., Nagel J., Spellmann H., Zasada M., Zingg A. Productivity of mixed versus pure stands of oak (Quercus petraea (Matt.) Liebl. and Quercus robur L.) and European beech (Fagus sylvatica L.) along an ecological gradient // European Journal of Forest Research. 2013. Vol. 132. No. 2. P. 263–280. DOI: 10.1007/s10342-012-0673-y.
Pretzsch H., Schütze G. Tree species mixing can increase stand productivity, density and growth efficiency and attenuate the trade-off between density and growth throughout the whole rotation // Annals of Botany. 2021. Vol. 128. No. 6. P. 767–786. DOI: 10.1093/aob/mcab077.
Priputina I. V., Frolova G. G., Shanin V. N., Myakshina T. N., Grabarnik P. Y. Spatial distribution of organic matter and nitrogen in the entic podzols of the Prioksko-Terrasnyi reserve and its relationship with the structure of forest phytocenoses // Eurasian Soil Science. 2020. Vol. 53. No. 8. P. 1021–1032. DOI: 10.1134/S1064229320080128.
Puhe J. Growth and development of the root system of Norway spruce (Picea abies) in forest stands — a review // Forest Ecology and Management. 2003. Vol. 175. No. 1–3. P. 253–273. DOI: 10.1016/S0378-1127(02)00134-2.
Pukkala T., Kolström T. A stochastic spatial regeneration model for Pinus sylvestris // Scandinavian Journal of Forest Research. 1992. Vol. 7. No. 1–4. P. 377–385. DOI: 10.1080/02827589209382730.
Pukkala T., Lähde E., Laiho O. Continuous cover forestry in Finland — Recent research results / Continuous cover Forestry, second ed. Pukkala T., von Gadow K. (eds.) Springer, 2012. P. 85–128. DOI: 10.1007/978-94-007-2202-6_3.
Püttsepp Ü., Lõhmus K., Persson H. Å., Ahlström K. Fine-root distribution and morphology in an acidic Norway spruce (Picea abies (L.) Karst.) stand in SW Sweden in relation to granulated wood ash application // Forest Ecology and Management. 2006. Vol. 221. No. 1–3. P. 291–298. DOI: 10.1016/j.foreco.2005.10.012.
R Core Team. R: a language and environment for statistical computing. R Foundation for Statistical Computing, 2014. URL: http://www.R-project.org/ (accessed on 31.08.2022).
Räim O., Kaurilind E., Hallik L., Merilo E. Why does needle photosynthesis decline with tree height in Norway spruce? // Plant Biology. 2012. Vol. 14. No. 2. P. 306–314. DOI: 10.1111/j.1438-8677.2011.00503.x.
Rankinen K., Karvonen T., Butterfield D. A simple model for predicting soil temperature in snow-covered and seasonally frozen soil: Model description and testing // Hydrology and Earth System Sciences. 2004. Vol. 8. No. 4. P. 706–716. DOI: 10.5194/hess-8-706-2004.
Ranney T. G., Bir R. E., Skroch W. A. Comparative drought resistance among six species of birch (Betula): influence of mild water stress on water relations and leaf gas exchange // Tree Physiology. 1991. Vol. 8. No. 4. P. 351–360. DOI: 10.1093/treephys/8.4.351.
Rautiainen M., Stenberg P. Simplified tree crown model using standard forest mensuration data for Scots pine // Agricultural and Forest Meteorology. 2005. Vol. 128. No. 1–2. P. 123–129. DOI: 10.1016/j.agrformet.2004.09.002.
Raynaud X., Leadley P. W. Symmetry of belowground competition in a spatially explicit model of nutrient competition // Ecological Modelling. 2005. Vol. 189. P. 447–453. DOI: 10.1016/j.ecolmodel.2005.03.008.
Renshaw E. Computer simulation of Sitka spruce: Spatial branching models for canopy growth and root structure // IMA Journal of Mathematics Applied in Medicine & Biology. 1985. Vol. 2. No. 3. P. 183–200. DOI: 10.1093/imammb/2.3.183.
Richards A. E., Forrester D. I., Bauhus J., Scherer‑Lorenzen M. The influence of mixed tree plantations on the nutrition of individual species: a review // Tree Physiology. 2010. Vol. 30. No. 9. P. 1192–1208. DOI: 10.1093/treephys/tpq035.
Romanov E. M., Nureeva T. V., Eremin N. V. The role of planted forests in improving the productive capacity and ecological potential of Scots pine boreal forests in the Middle Volga Region // New Zealand Journal of Forestry Science. 2016. Vol. 46. ID 10. DOI: 10.1186/s40490-016-0066-y.
Rothe A., Binkley D. Nutritional interactions in mixed species forests: a synthesis // Canadian Journal of Forest Research. 2001. Vol. 31. No. 11. P. 1855–1870. DOI: 10.1139/x01-120.
Rötzer T. Mixing patterns of tree species and their effects on resource allocation and growth in forest stands // Nova Acta Leopoldina. 2013. Vol. 114. No. 391. P. 239–254.
Rötzer T., Liao Y., Goergen K., Schüler G., Pretzsch H. Modelling the impact of climate change on the productivity and water-use efficiency of a central European beech forest // Climate Research. 2013. Vol. 58. No. 1. P. 81–95. DOI: 10.3354/cr01179.
Rust S., Savill P. S. The root systems of Fraxinus excelsior and Fagus sylvatica and their competitive relationships // Forestry: an International Journal of Forest Research. 2000. Vol. 73. No. 5. P. 499–508. DOI: 10.1093/forestry/73.5.499.
Saxton K. E., Rawls W. J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions // Soil Science Society of America Journal. 2006. Vol. 70. No. 5. P. 1569–1578. DOI: 10.2136/sssaj2005.0117.
Schaetzl R. J., Knapp B. D., Isard S. A. Modeling soil temperatures and the mesic‐frigid boundary in the central Great Lakes region, 1951–2000 // Soil Science Society of America Journal. 2005. Vol. 69. No. 6. P. 2033–2040. DOI: 10.2136/sssaj2004.0349.
Schiffers K., Tielbörger K., Tietjen B., Jeltsch F. Root plasticity buffers competition among plants: theory meets experimental data // Ecology. 2011. Vol. 92. No. 3. P. 610–620. DOI: 10.1890/10-1086.1.
Schmid I. The influence of soil type and interspecific competition on the fine root system of Norway spruce and European beech // Basic and Applied Ecology. 2002. Vol. 3. No. 4. P. 339–346. DOI: 10.1078/1439-1791-00116.
Schmid I., Kazda M. Root distribution of Norway spruce in monospecific and mixed stands on different soils // Forest Ecology and Management. 2002. Vol. 159. No. 1–2. P. 37–47. DOI: 10.1016/S0378-1127(01)00708-3.
Schröter M., Härdtle W., von Oheimb G. Crown plasticity and neighborhood interactions of European beech (Fagus sylvatica L.) in an old-growth forest // European Journal of Forest Research. 2012. Vol. 131. P. 787–798. DOI: 10.1007/s10342-011-0552-y.
Seidel D., Leuschner C., Müller A., Krause K. Crown plasticity in mixed forests — Quantifying asymmetry as a measure of competition using terrestrial laser scanning // Forest Ecology and Management. 2011. Vol. 261. No. 11. P. 2123–2132. DOI: 10.1016/j.foreco.2011.03.008.
Seidl R., Lexer M. J., Jäger D., Hönninger K. Evaluating the accuracy and generality of a hybrid patch model // Tree Physiology. 2005. Vol. 25. No. 7. P. 939–951. DOI: 10.1093/treephys/25.7.939.
Seidl R., Rammer W., Scheller R. M., Spies T. A. An individual-based process model to simulate landscape-scale forest ecosystem dynamics // Ecological Modelling. 2012. Vol. 231. P. 87–100. DOI: 10.1016/j.ecolmodel.2012.02.015.
Shanin V. N., Grabarnik P. Y., Shashkov M. P., Ivanova N. V., Bykhovets S. S., Frolov P. V., Stamenov M. N. Crown asymmetry and niche segregation as an adaptation of trees to competition for light: conclusions from simulation experiments in mixed boreal stands // Mathematical and Computational Forestry and Natural-Resource Sciences. 2020. Vol. 12. No. 1. P. 26–49. DOI: 10.5281/zenodo.3759256.
Shanin V., Hökkä H., Grabarnik P. Testing the performance of some competition indices against experimental data and outputs of spatially-explicit simulation models // Forests. 2021a. Vol. 12. No. 10. ID 1415. DOI: 10.3390/f12101415.
Shanin V., Juutinen A., Ahtikoski A., Frolov P., Chertov O., Rämö J., Lehtonen A., Laiho R., Mäkiranta P., Nieminen M., Laurén A., Sarkkola S., Penttilä T., Ťupek B., Mäkipää R. Simulation modelling of greenhouse gas balance in continuous-cover forestry of Norway spruce stands on nutrient-rich drained peatlands // Forest Ecology and Management. 2021b. Vol. 496. ID 119479. DOI: 10.1016/j.foreco.2021.119479.
Shanin V., Mäkipää R., Shashkov M., Ivanova N., Shestibratov K., Moskalenko S., Rocheva L., Grabarnik P., Bobkova K., Manov A., Osipov A., Burnasheva E., Bezrukova M. New procedure for the simulation of belowground competition can improve the performance of forest simulation models // European Journal of Forest Research. 2015a. Vol. 134. P. 1055–1074. DOI: 10.1007/s10342-015-0909-8.
Shanin V. N., Rocheva L. K., Shashkov M. P., Ivanova N. V., Moskalenko S. V., Burnasheva E. R. Spatial distribution of root biomass of certain tree species (Picea abies, Pinus sylvestris, Betula sp.) // Biology Bulletin of the Russian Academy of Sciences. 2015b. Vol. 42. No. 3. P. 260–268. DOI: 10.1134/S1062359015030115.
Shashkov M. P., Bobrovsky M. V., Shanin V. N., Khanina L. G., Grabarnik P. Y., Stamenov M. N., Ivanova N. V. Data on 30‑year stand dynamics in an old-growth broad-leaved forest in the Kaluzhskie Zaseki State Nature Reserve, Russia // Nature Conservation Research. 2022. Vol. 7. Suppl. 1. P. 24–37. DOI: 10.24189/ncr.2022.013.
Shorohova E., Kapitsa E. Influence of the substrate and ecosystem attributes on the decomposition rates of coarse woody debris in European boreal forests // Forest Ecology and Management. 2014. Vol. 315. P. 173–184. DOI: 10.1016/j.foreco.2013.12.025.
Shugart H. H., Leemans R., Bonan G. B. A system analysis of the global boreal forest. Cambridge University Press, 1992. 580 p. DOI: 10.1017/CBO9780511565489.
Sievänen R., Perttunen J., Nikinmaa E., Kaitaniemi P. Toward extension of a single tree functional-structural model of Scots pine to stand level: Effect of the canopy of randomly distributed, identical trees on development of tree structure // Functional Plant Biology. 2008. Vol. 35. No. 10. P. 964–975. DOI: 10.1071/FP08077.
Sinkkonen A. Red reveals branch die-back in Norway maple Acer platanoides // Annals of Botany. 2008. Vol. 102. No. 3. P. 361–366. DOI: 10.1093/aob/mcn101.
Skarvelis M., Mantanis G. Physical and mechanical properties of beech wood harvested in the Greek public forests // Wood Research. 2013. Vol. 58. No. 1. P. 123–130.
Spielvogel S., Prietzel J., Auerswald K., Kogel‑Knabner I. Site-specific spatial patterns of soil organic carbon stocks in different landscape units of a high-elevation forest including a site with forest dieback // Geoderma. 2009. Vol. 152. No. 3–4. P. 218–230. DOI: 10.1016/j.geoderma.2009.03.009.
Šrámek M., Čermák J. The vertical leaf distribution of Ulmus laevis Pall. // Trees. 2012. Vol. 26. P. 1781–1792. DOI: 10.1007/s00468-012-0747-y.
Stadt K. J., Lieffers V. J. MIXLIGHT: a flexible light transmission model for mixed-species forest stands // Agricultural and Forest Meteorology. 2000. Vol. 102. No. 4. P. 235–252. DOI: 10.1016/S0168-1923(00)00128-3.
Stanley R. P. Differential posets // Journal of the American Mathematical Society. 1988. Vol. 1. No. 4. P. 919–961. DOI: 10.2307/1990995.
Starr M., Helmisaari H.‑S., Merilä P. Modeling rooting depth and distribution from incomplete profile root biomass data // “Roots to the Future”. 8th Symposium of the International Society of Root Research, 26–29 June 2012, Dundee, Scotland. P. 52.
Starr M., Palviainen M., Finér L., Piirainen S., Mannerkoski H. Modelling rooting depth of trees in boreal forests // Abstracts of International Symposium “Root Research and Applications” RootRAP, 2–4 September 2009, Boku Vienna, Austria, 2009. P. 1–2.
Steffens C., Helfrich M., Joergensen R. G., Eissfeller V., Flessa H. Translocation of 13C‑labeled leaf or root litter carbon of beech (Fagus sylvatica L.) and ash (Fraxinus excelsior L.) during decomposition — a laboratory incubation experiment // Soil Biology and Biochemistry. 2015. Vol. 83. P. 125–137. DOI: 10.1016/j.soilbio.2015.01.015.
Strong W. L., La Roi G. H. Root density — soil relationships in selected boreal forests of central Alberta, Canada // Forest Ecology and Management. 1985. Vol. 12. No. 3–4. P. 233–251. DOI: 10.1016/0378-1127(85)90093-3.
Strous L. Astronomy answers. URL: https://aa.quae.nl/en/index.html (accessed on 03.10.2022)
Suvorova G., Korzukhin M., Ivanova M. Influence of environmental factors on photosynthesis of three coniferous species // Annual Research & Review in Biology. 2017. Vol. 12. No. 3. P. 1–14. DOI: 10.9734/ARRB/2017/31526.
Sverdrup H., Belyazid S., Nilgard B., Ericson L. Modelling change in ground vegetation response to acid and nitrogen pollution, climate change and forest management // Water, Air & Soil Pollution. 2007. Vol. 7. P. 163–179. DOI: 10.1007/s11267-006-9067-9.
Swenson J. J., Waring R. H., Fan W., Coops N. Predicting site index with a physiologically based growth model across Oregon, USA // Canadian Journal of Forest Research. 2005. Vol. 35. No. 7. P. 1697–1707. DOI: 10.1139/x05-089.
Tahvanainen T., Forss E. Individual tree models for the crown biomass distribution of Scots pine, Norway spruce and birch in Finland // Forest Ecology and Management. 2008. Vol. 255. No. 3–4. P. 455–467. DOI: 10.1016/j.foreco.2007.09.035.
Tahvonen O., Rämö J. Optimality of continuous cover vs. clear-cut regimes in managing forest resources // Canadian Journal of Forest Research. 2016. Vol. 46. No. 7. P. 891–901. DOI: 10.1139/cjfr-2015-0474.
Takenaka C., Miyahara M., Ohta T., Maximov T. C. Response of larch root development to annual changes of water conditions in Eastern Siberia // Polar Science. 2016. Vol. 10. No. 2. P. 160–166. DOI: 10.1016/j.polar.2016.04.012.
Tanskanen N., Ilvesniemi H. Spatial distribution of fine roots at ploughed Norway spruce forest sites // Silva Fennica. 2007. Vol. 41. No. 1. P. 45–54. DOI: 10.14214/sf.306.
Tardío G., González‑Ollauri A., Mickovski S. B. A non-invasive preferential root distribution analysis methodology from a slope stability approach // Ecological Engineering. 2016. Vol. 97. P. 46–57. DOI: 10.1016/j.ecoleng.2016.08.005.
Tatarinov F., Urban J., Čermák J. Application of “clump technique” for root system studies of Quercus robur and Fraxinus excelsior // Forest Ecology and Management. 2008. Vol. 255. No. 3–4. P. 495–505. DOI: 10.1016/j.foreco.2007.09.022.
Teichmann J., Ballani F., van den Boogaart K. G. Generalizations of Matérn’s hard-core point processes // Spatial Statistics. 2013. Vol. 3. P. 33–53. DOI: 10.1016/j.spasta.2013.02.001.
Thomas F. M., Bögelein R., Werner W. Interaction between Douglas fir and European beech — Investigations in pure and mixed stands // Forstarchiv. 2015. Vol. 86. No. 4. P. 83–91. DOI: 10.4432/0300-4112-86-83.
Thomas F. M., Hartmann G. Tree rooting patterns and soil water relations of healthy and damaged stands of mature oak (Quercus robur L. and Quercus petraea [Matt.] Liebl.) // Plant and Soil. 1998. Vol. 203. P. 145–158. DOI: 10.1023/A:1004305410905.
Thomas P. A., Stone D., La Porta N. Biological flora of the British Isles: Ulmus glabra // Journal of Ecology. 2018. Vol. 106. No. 4. P. 1724–1766. DOI: 10.1111/1365-2745.12994.
Thorpe H. C., Astrup R., Trowbridge A., Coates K. D. Competition and tree crowns: a neighborhood analysis of three boreal tree species // Forest Ecology and Management. 2010. Vol. 259. No. 8. P. 1586–1596. DOI: 10.1016/j.foreco.2010.01.035.
Thurm E. A., Biber P., Pretzsch H. Stem growth is favored at expenses of root growth in mixed stands and humid conditions for Douglas-fir (Pseudotsuga menziesii) and European beech (Fagus sylvatica) // Trees. 2017. Vol. 31. No. 1. P. 349–365. DOI: 10.1007/s00468-016-1512-4.
Toïgo M., Vallet P., Perot T., Bontemps J.‑D., Piedallu C., Courbaud B. Overyielding in mixed forests decreases with site productivity // Journal of Ecology. 2015. Vol. 103. No. 2. P. 502–512. DOI: 10.1111/1365-2745.12353.
Tomczak A., Jelonek T., Jakubowski M. Modulus of elasticity of twin samples (wet and absolute dry) origin from Scots pine (Pinus sylvestris L.) trees broken by wind // Annals of Warsaw University of Life Sciences — SGGW Forestry and Wood Technology. 2011. Vol. 76. P. 149–153.
Tran Q. T., Tainar D., Safar M. Reverse k nearest neighbor and reverse farthest neighbor search on spatial networks / Transactions on large-scale data- and knowledge-centered systems / Hameurlain I., Küng J., Wagner R. (eds.). Springer, 2009. P. 353–372. DOI: 10.1007/978-3-642-03722-1.
Trémolières M., Schnitzler A., Sánchez‑Pérez J.‑M., Schmitt D. Changes in foliar nutrient content and resorption in Fraxinus excelsior L., Ulmus minor Mill. and Clematis vitalba L. after prevention of floods // Annals of Forest Science. 1999. Vol. 56. No. 8. P. 641–650. DOI: 10.1051/forest:19990802.
Urban J., Čermák J., Ceulemans R. Above- and below-ground biomass, surface and volume, and stored water in a mature Scots pine stand // European Journal of Forest Research. 2015. Vol. 134. P. 61–74. DOI: 10.1007/s10342-014-0833-3.
Uri V., Kukumägi M., Aosaar J., Varik M., Becker H., Aun K., Krasnova A., Morozov G., Ostonen I., Mander Ü., Lõhmus K., Rosenvald K., Kriiska K., Soosaar K. The carbon balance of a six-year-old Scots pine (Pinus sylvestris L.) ecosystem estimated by different methods // Forest Ecology and Management. 2019. Vol. 433. P. 248–262. DOI: 10.1016/j.foreco.2018.11.012.
Uri V., Varik M., Aosaar J., Kanal A., Kukumägi M., Lõhmus K. Biomass production and carbon sequestration in a fertile silver birch (Betula pendula Roth) forest chronosequence // Forest Ecology and Management. 2012. Vol. 267. P. 117–126. DOI: 10.1016/j.foreco.2011.11.033.
van der Hage J. C. H. The horizontal component of solar radiation // Agricultural and Forest Meteorology. 1993. Vol. 67. No. 1–2. P. 79–93. DOI: 10.1016/0168-1923(93)90051-I.
Vergarechea M., del Río M., Gordo J., Martín R., Cubero D., Calama R. Spatio-temporal variation of natural regeneration in Pinus pinea and Pinus pinaster Mediterranean forests in Spain // European Journal of Forest Research. 2019. Vol. 138. P. 313–326. DOI: 10.1007/s10342-019-01172-8.
Veselkin D. V. Distribution of fine roots of coniferous trees over the soil profile under conditions of pollution by emissions from a copper-smelting plant // Russian Journal of Ecology. 2002. Vol. 33. No. 4. P. 231–234. DOI: 10.1023/A:1016208118629.
Vesterdal L., Schmidt I. K., Callesen I., Nilsson L. O., Gundersen P. Carbon and nitrogen in forest floor and mineral soil under six common European tree species // Forest Ecology and Management. 2008. Vol. 255. No. 1. P. 35–48. DOI: 10.1016/j.foreco.2007.08.015.
Viherä‑Aarnio A., Velling P. Growth, wood density and bark thickness of silver birch originating from the Baltic countries and Finland in two Finnish provenance trials // Silva Fennica. 2017. Vol. 51. No. 4. ID 7731. DOI: 10.14214/sf.7731.
von der Heide-Spravka K. G., Watson G. W. Directional differences in little-leaf linden (Tilia cordata Mill.) crown development // Arboricultural Journal. 1992. Vol. 16. No. 3. P. 243–252. DOI: 10.1080/03071375.1992.9746922.
Wambsganss J., Beyer F., Freschet G. T., Scherer‑Lorenzen M., Bauhus J. Tree species mixing reduces biomass but increases length of absorptive fine roots in European forests // Journal of Ecology. 2021. Vol. 109. No. 7. P. 2678–2691. DOI: 10.1111/1365-2745.13675.
Wang W., Peng C., Zhang S. Y., Zhou X., Larocque G. R., Kneeshaw D. D., Lei X. Development of TRIPLEX-Management model for simulating the response of forest growth to pre-commercial thinning // Ecological Modelling. 2011. Vol. 222. No. 14. P. 2249–2261. DOI: 10.1016/j.ecolmodel.2010.09.019.
Watt A. S. Pattern and process in the plant community // Journal of Ecology. 1947. Vol. 35. No. 1/2. P. 1–22. DOI: 10.2307/2256497.
Way D. A., Domec J.-C., Jackson R. B. Elevated growth temperatures alter hydraulic characteristics in trembling aspen (Populus tremuloides) seedlings: Implications for tree drought tolerance // Plant, Cell & Environment. 2013. Vol. 36. No. 1. P. 103–115. DOI: 10.1111/j.1365-3040.2012.02557.x.
Weemstra M., Sterck F. J., Visser E. J. W., Kuyper T. W., Goudzwaard L., Mommer L. Fine-root trait plasticity of beech (Fagus sylvatica) and spruce (Picea abies) forests on two contrasting soils // Plant and Soil. 2017. Vol. 415. No. 1–2. P. 175–188. DOI: 10.1007/s11104-016-3148-y
Widlowski J.-L., Verstraete M., Pinty B., Gobron N. Allometric relationships of selected European tree species. Technical Report EUR 20855 EN. EC Joint Research Centre, 2003. 61 p.
Wiegand T., Martínez I., Huth A. Recruitment in tropical tree species: revealing complex spatial patterns // The American Naturalist. 2009. Vol. 174. No. 4. P. E106–E140. DOI: 10.1086/605368.
Williams T. G., Flanagan L. B. Effect of changes in water content on photosynthesis, transpiration and discrimination against 13CO2 and C18O16O in Pleurozium and Sphagnum // Oecologia. 1996. Vol. 108. No. 1. P. 38–46. DOI: 10.1007/BF00333212.
Withington J. M., Reich P. B., Oleksyn J., Eissenstat D. M. Comparisons of structure and life span in roots and leaves among temperate trees // Ecological Monographs. 2006. Vol. 76. No. 3. P. 381–397. DOI: 10.1890/0012-9615(2006)076[0381:COSALS]2.0.CO;2.
WRB, 2015. World Reference Base for Soil Resources 2014, update 2015. International soil classification system for naming soils and creating legends for soil maps. World Soil Resources Reports No. 106. FAO, Rome.
Wullschleger S. D., Hanson P. J. Sensitivity of sapling and mature-tree water use to altered precipitation regimes / North American temperate deciduous forest responses to changing precipitation regimes. Hanson P. J., Wullschleger S. D. (eds.) Springer, 2003. P. 87–98. DOI: 10.1007/978-1-4613-0021-2.
Yastrebov A. B. Different types of heterogeneity and plant competition in monospecific stands // Oikos. 1996. Vol. 75. No. 1. P. 89–97. DOI: 10.2307/3546325.
Yen Y. C. Effective thermal conductivity of ventilated snow // Journal of Geophysical Research. 1962. Vol. 67. No. 3. P. 1091–1098. DOI: 10.1029/JZ067i003p01091.
Yen Y. C. Review of thermal properties of snow, ice, and sea ice. Cold Regions Research and Engineering Laboratory, Report 81–10. US Army, Corps of Engineers, 1981. 35 p.
Yu X., Wu Z., Jiang W., Guo X. Predicting daily photosynthetically active radiation from global solar radiation in the Contiguous United States // Energy Conversion and Management. 2015. Vol. 89. P. 71–82. DOI: 10.1016/j.enconman.2014.09.038.
Yuan Z. Y., Chen H. Y. H. Fine root biomass, production, turnover rates, and nutrient contents in boreal forest ecosystems in relation to species, climate, fertility, and stand age: literature review and meta-analyses // Critical Reviews in Plant Sciences. 2010. Vol. 29. No. 4. P. 204–221. DOI: 10.1080/07352689.2010.483579.
Zadworny M., McCormack M. L., Rawlik K., Jagodziński A. M. Seasonal variation in chemistry, but not morphology, in roots of Quercus robur growing in different soil types // Tree Physiology. 2015. Vol. 35. No. 6. P. 644–652. DOI: 10.1093/treephys/tpv018.
Zagirova S. V. Structure and CO2 exchange in the needles of Pinus sylvestris and Abies sibirica // Russian Journal of Plant Physiology. 2001. Vol. 48. No. 1. P. 23–28. DOI: 10.1023/A:1009086211938.
Zajączkowska U., Kozakiewicz P. Interaction between secondary phloem and xylem in gravitropic reaction of lateral branches of Tilia cordata Mill. trees // Holzforschung. 2016. Vol. 70. No. 10. P. 993–1002. DOI: 10.1515/hf-2015-0230.
Zhang C., Stratopoulos L. M. F., Pretzsch H., Rötzer T. How do Tilia cordata Greenspire trees cope with drought stress regarding their biomass allocation and ecosystem services? // Forests. 2019. Vol. 10. No. 8. ID 676. DOI: 10.3390/f10080676.
Zhang S.‑Y., Owoundi R. E., Nepveu G., Mothe F., Dhôte J.‑F. Modelling wood density in European oak (Quercus petraea and Quercus robur) and simulating the silvicultural influence // Canadian Journal of Forest Research. 1993. Vol. 23. No. 12. P. 2587–2593. DOI: 10.1139/x93-320.
Zheng D., Hunt Jr E. R., Running S. W. A daily soil temperature model based on air temperature and precipitation for continental applications // Climate Research. 1993. Vol. 2. No. 3. P. 183–191. DOI: 10.3354/cr002183.
Zhou X., Peng C., Dang Q.‑L., Sun J., Wu H., Hua D. Simulating carbon exchange in Canadian boreal forests. I. Model structure, validation, and sensitivity analysis // Ecological Modelling. 2008. Vol. 219. No. 3–4. P. 287–299. DOI: 10.1016/j.ecolmodel.2008.07.011.
Zhu G.‑F., Li X., Su Y.‑H., Lu L., Huang C.‑L., Niinemets Ü. Seasonal fluctuations and temperature dependence in photosynthetic parameters and stomatal conductance at the leaf scale of Populus euphratica Oliv. // Tree Physiology. 2011. Vol. 31. No. 2. P. 178–195. DOI: 10.1093/treephys/tpr005.
Zhu Y., Zhang H., Gao Y., Dilixiati B., Ding C., Yang Y. Analysis on carbon content factors of Larix sibirica Ledeb. in Xinjiang // Journal Of Nanjing Forestry University. 2017. Vol. 60. No. 3. P. 198–202.
Рецензент: к. ф.-м. н. Колобов А. Н.





